An Expected Value
Tamara chooses an integer x uniformly at random from 1 to 4 2 5 . She then chooses an integer y uniformly at random from 1 , 2 , … , x . What is the expected value of y ?
The answer is 107.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
For a given x , E ( y ) = x ∑ i = 1 x i = x 2 x ( x + 1 ) = 2 x + 1 .
Since x is uniform randomly selected from integers in [ 1 , 4 2 5 ] , the probability that x takes on any unique integer value in the specified interval is 4 2 5 1 .
Consequently we have E ( y ) = 4 2 5 ∑ n = 1 4 2 5 2 n + 1 = 8 5 0 ∑ n = 1 4 2 5 n + 1 = 8 5 0 2 4 2 5 × 4 2 6 + 4 2 5 = 2 2 1 × 4 2 6 + 1 = 2 2 1 4 = 1 0 7 .
I don't understand any of these weird signs in your solution but I still managed to solve the problem.
Jajaja, I just don't get anything. After reafing this I'd still saying X=4 because Y is a ranfom uniform number from 1,2,...,x, therefore, if there is only one gap from 2 to x means y=3 and x=4 😂😂 Does it make sense to you?
The expected value of y for a given x is (x+1)/2. Sum this for 1<=x<=425, and divide by 425 to get the overall average. Here are some terms: 1/425*(1+1.5+2+... 426/2). There are 425 terms, each term averaging 214/2 (pair up the first and last terms, 2nd & 424th etc), so the total is 214/2 = 107.
When Tamara chooses the number x , the expected value of y is 2 x + 1 . Thus, the expected value of y is the expected value of 2 x + 1 as x ranges uniformly from 1 to 4 2 5 . By linearity of expectation, E [ y ] = E [ 2 x + 1 ] = 2 E [ x ] + 1 . Since E [ x ] = 2 4 2 5 + 1 = 2 1 3 , hence E [ y ] = 2 2 1 3 + 1 = 1 0 7 .
What is the topic of this subject?
Log in to reply
The topic is already stated to be Combinatorics.
If you want to know the skill, you can click on "What do I need to know" or "Learn how to solve problems like this".

Log in to reply
I mean the subtopics.
Log in to reply
@Figel Ilham – If you click on the links, it will bring you down to the exact skill, and you can thus get the subtopic and chapter.
Log in to reply
@Calvin Lin – Okay, thanks sir. But it says Brilliant2. Do you have any other ways to become Brilliant 2 instead of using the plastic? Maybe voucher or transfer?
Log in to reply
@Figel Ilham – You should still be able to click on it, and it (currently) will redirect you to the skill. For a non B^2 member, you would see:
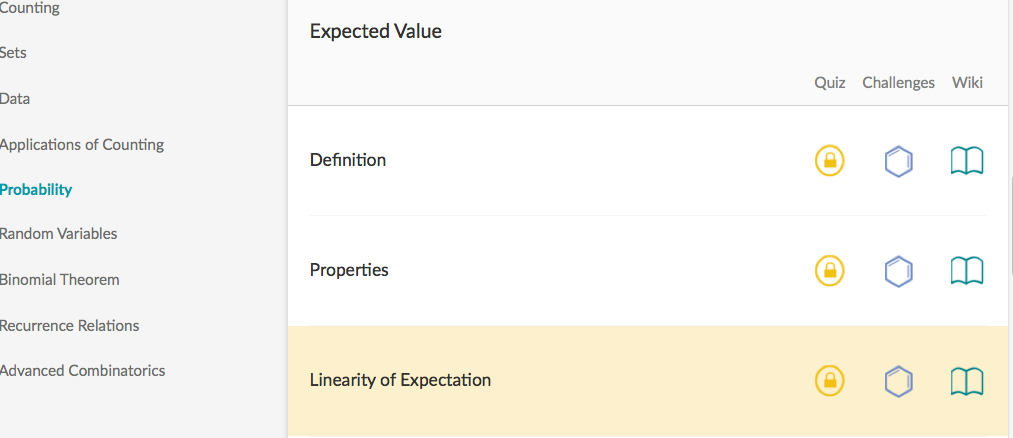
Hence, it is Combinatorics -> Probability -> Expected Value -> Linearity of Expectation. (Note that not all problems have this functionality, just the popular ones.)
Finally a well explained answer!!
By Iterated Expectation theorem:
E [ Y ] = E [ E [ Y ∣ X ] ]
Considering this problem,
E [ Y ∣ X = x ] = 2 1 + x
(The above is true because Y is Uniform Distribution which takes values between 1 and x .
In general the expected value of random variable X having Uniform Distribution is 2 a + b where X takes values from a to b .)
Therefore, in general case where X can take any value,
E [ Y ∣ X ] = 2 1 + X
Now,
E [ Y ] = E [ E [ Y ∣ X ] ]
= E [ 2 1 + X ] = 2 1 + 2 1 E [ X ]
(by Linearity of Expectation )
= 0 . 5 + 0 . 5 ∗ 2 1 + 4 2 5 = 1 0 7
4 a + 3 where a = 425
Generally, when L is number of chooses (how deep): 2 L a + 2 L − 1
Firstly, to find the expected value of x, I multiplied the probability of each number being picked by the value of that number. Since each number has the probability of being picked P(x) = 1/425, and retains its own integer value, the expected value of x is (1/425) (1 + 2 + 3 ... + 424 + 425) = (425 426)/(425*2) = 213.
Essentially doing the same process with y except now P(y) = 1/213, we get the expected value of y as (1/213) * (1 + 2 + 3 + .... + 212 + 213) = (213 214)/(213 2) = 107.
Therefore the EV of y is 107.
First of all we need to find E ( x ) . E ( x ) = ( 1 + 2 + 3 + . . . . . . . . . . . . + 4 2 5 ) / 4 2 5 = ( 4 2 5 ∗ 4 2 6 ) / ( 2 ∗ 4 2 5 ) = 2 1 3 . Now, E ( y ) = ( 1 + 2 + 3 + . . . . . . . . . . + 2 1 3 ) / 2 1 3 = ( 2 1 3 ∗ 2 1 4 ) / ( 2 ∗ 2 1 3 ) = 1 0 7 . Hence the expected value of y = 1 0 7 .
This is the most common mistake made, which shows that students didn't understand the concept of expected value. They claim that "the expected value of
X
is 213 ), hence
E
(
Y
)
=
(
1
+
2
+
…
+
2
1
3
)
/
2
1
3
."
On what basis is this claim true?
What happens if the expected value of
X
is 212.5 instead (like when we chose an integer from 1 to 424?
How do we stop taking the sum at a half integer?
If a random variable is uniformly distributed in { 1 , 2 , … , n } , then its expected value is given by ∑ k = 1 n n k = 2 n + 1 . Then, we use that to write E [ Y ] = E [ E [ Y ∣ X ] ] = E [ 2 1 + X ] = 2 1 + 2 1 + 4 2 5 = 1 0 7 .
To find the expected value of x, you must find the median value of x: \frac {415 + 1}{2} = 213 Now, we do the same to find the expected value of y: \frac {213 + 1}{2} = 107 Therefore, the expected value for y is 107.
The expected value of x = 2 1 + 4 2 5 = 2 1 3 then the expected value of y = 2 1 + 2 1 3 = 1 0 7
Here we have to understand the language of problem statement. Choosing a random number from 1 to 425, "UNIFORMLY". Here uniformly means at constant differences. So the series formed will be A.P
Hence applying (x)=(d/2) (2 a+(n-1)*d) where S(x) is the sum of series up-to n d is the constant difference.
Here, S(x)=(1/2) (2 1+(425-1)*1)=213
Now, Once again we have to repeat the process, because selection of number choosing "UNIFORMLY" at random is repeated for new value of n(previous result). S'(x)=(1/2) (2 1+(213-1)*1)=107
here, we have answer as 107.
* The same problem can be for other than uniformly, it can be G.P
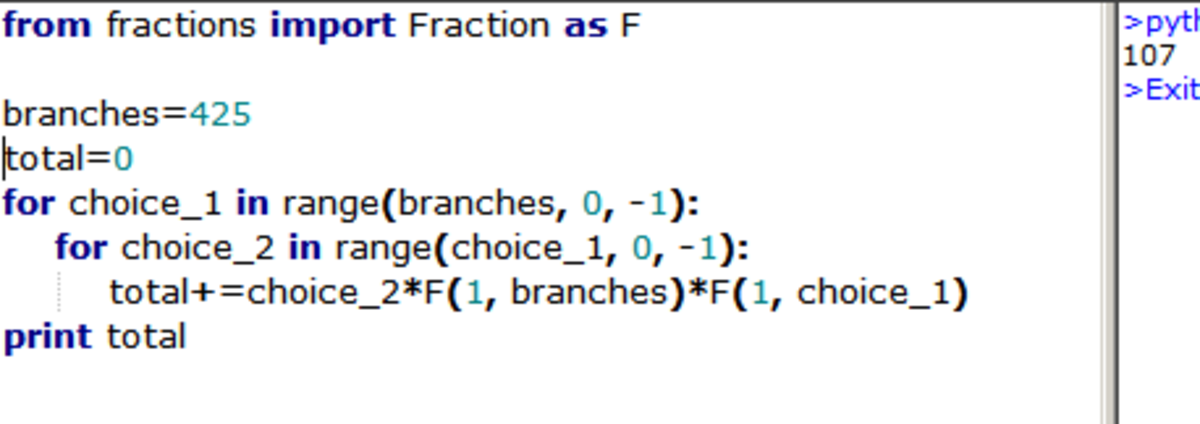
Tamara can choose 4 2 5 numbers from 1 to 4 2 5 .
Let x i denote the number selected such that x 1 = 1 , … , x 4 2 5 = 4 2 5 .
The expected value of y is the average of all the expected values of y i for every corresponding x i .
We calculate that E ( y 1 ) = 1 , E ( y 2 ) = 1 . 5 , E ( y 3 ) = 2 , . . . . , E ( y 4 2 5 ) = 2 1 3
And,
E ( y ) = 4 2 5 1 i = 1 ∑ 4 2 5 E ( y i )
E ( y ) = 4 2 5 1 ⋅ 4 2 5 ⋅ ( 2 1 + 2 1 3 ) [Note that the summation yields this expression since first term is 1 and the last 4 2 5 with common difference 0 . 5 ].
Hence, E ( y ) = 1 0 7