An interesting Curve
Given an ellipse (in blue) with a horizontal major axis of length 10 and a vertical minor axis of length 6, we construct a curve (in red) which is the boundary of the convex hull of points which are 3 units away from the blue ellipse.
Find the length of this red curve, and find the area of the band with width 3 (shaded in light blue) around the ellipse.
If S is the sum of these two numbers, then submit ⌊ 1 0 0 0 S ⌋ as your answer.
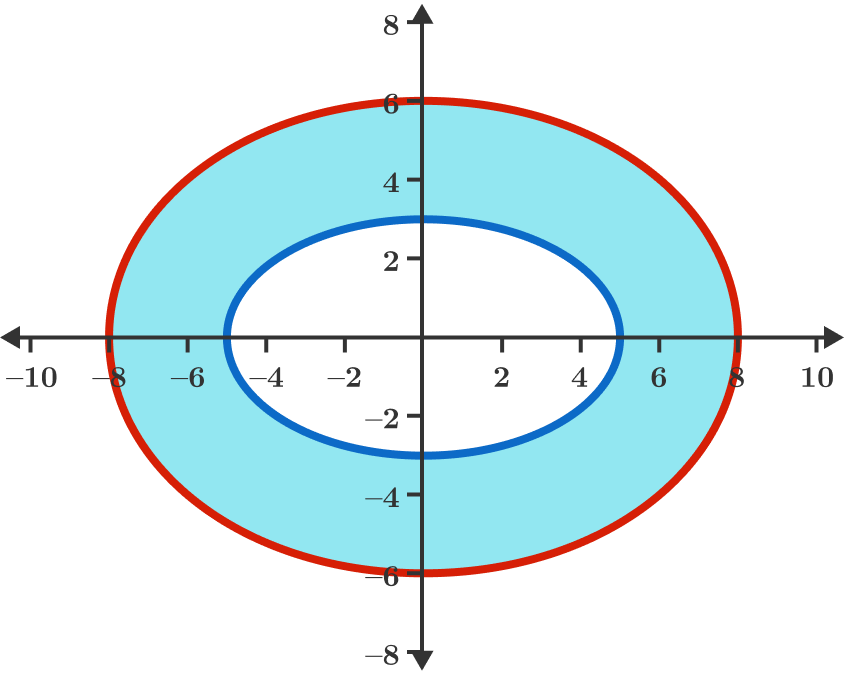
The answer is 149231.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
I want to know if the red curve is an eclipse .
Log in to reply
No, it is not.
Log in to reply
why? i really dont understand why?
Log in to reply
@Tsuriel Avraham – ( − 4 , 5 9 ) is a point on the blue curve. The blue curve has slope 5 4 at this point, so we can draw a length three perpendicular with slope 4 − 5 from this point. We then get that the point ( − 4 − 4 1 1 2 , 5 9 + 4 1 1 5 ) is on the red curve. If the red curve was an ellipse, then its equation would be 6 4 x 2 + 3 6 y 2 = 1 , but the point we found does not satisfy that equation, so we know that the red curve is not an ellipse.
quite an elegant solution it is! a simple but cute geometric shortcut and a piece of simple calculus! thanks for publishing that!
But i think the area is 33π(48π-15π)
More generally, suppose we start with a curve α , and construct a curve β that has a distance of r from α . Then Length ( β ) = Length ( α ) + 2 π r and Area ( β ) = Area ( α ) + r ⋅ Length ( α ) + π r 2 .
See https://math.stackexchange.com/questions/58467/a-question-on-closed-convex-plane-curves-from-do-carmo . You can get some intuition for this result by considering the case where α is a polygon.
Very cool formulas but using them I get that S=47pi, which is actually rather close to the expected value of S being approximately 47.5017pi but still off. I found the areas of both of the ellipses (A=ab*pi) and used the areas along with these formulas to find the lengths.
Log in to reply
Just to make it clear, only the original blue curve is an ellipse. The outer red curve is not an ellipse.
Is there any analogous formula for surface area and volume in three dimensions?
The parametric equation of the given ellipse is
p ( t ) = ( 5 cos t , 3 sin t )
The tangent vector is given by
p ′ ( t ) = ( − 5 sin t , 3 cos t )
Therefore, the unit normal is given by
n ( t ) = ( 3 cos t , 5 sin t ) / 9 cos 2 t + 2 5 sin 2 t
It follows that
q ( t ) = ( 5 cos t , 3 sin t ) + 3 ( 3 cos t , 5 sin t ) / 9 cos 2 t + 2 5 sin 2 t
The derivative with respect to t is given by
q ′ ( t ) = ( − 5 sin t , 3 cos t ) + 3 ( − 3 sin t , 5 cos t ) / 9 cos 2 t + 2 5 sin 2 t − 3 ( 3 cos t , 5 sin t ) ( − 9 cos t sin t + 2 5 sin t cos t ) / ( 9 cos 2 t + 2 5 sin 2 t ) ( 3 / 2 )
= ( − 5 sin t , 3 cos t ) + 3 ( − 3 sin t , 5 cos t ) / 9 cos 2 t + 2 5 sin 2 t − 3 ( 3 cos t , 5 sin t ) ( 8 sin 2 t ) / ( 9 cos 2 t + 2 5 sin 2 t ) ( 3 / 2 )
To find the length of the curve, we integrate the length of q ′
L = ∫ 0 2 π ∣ q ′ ( t ) ∣ d t
And the area enclosed by the curve is given by
A = 2 1 ∣ ∫ 0 2 π ( q x q ′ y − q y q ′ x ) d t ∣
These integrations can be carried out very easily and accurately using Simpson's Rule numerical integration method, and the result is
L = 4 4 . 3 7 6 5 5 and A = 1 5 1 . 9 7 9 2 2 , thus the area of the blue-shaded band is A − π ( 5 ) ( 3 ) = 1 0 4 . 8 5 5 3 3 , and this makes the answer
⌊ 1 0 0 0 ( 4 4 . 3 7 6 5 5 + 1 0 4 . 8 5 5 3 3 ) ⌋ = ⌊ 1 0 0 0 ( 1 4 9 . 2 3 1 8 8 ) ⌋ = 1 4 9 2 3 1
The figure says horizontal r=4, the text says r=5?
Where do you get the formula for area from?
Log in to reply
It follows from a modification of Green's theorem to find the area enclosed by a closed curve. Refer to any textbook on Calculus, and you should find the answer to your question.
Concentrating on the first quadrant, the ellipse is y = 3 1 − 2 5 x 2
The normal as a function of x is the opposite reciprocal of the derivative N ( x ) = 9 x 2 6 2 5 − 9 2 5
For any ( x , y ) on the ellipse, we can now add the correct amount of this normal to each coordinate to get a new point on the outer rim ( x + 1 + N 2 3 , y + 1 + N 2 3 N )
Now let x and y each be mediated by parameter a where x = a + 6 2 5 − 1 6 a 2 9 a and y = 3 1 − 2 5 a 2 ( 1 + 6 2 5 − 1 6 a 2 2 5 )
This is where I leave out some gory details. From here I leaned heavily on WolframAlpha. Find d x and d y easily enough.
The area can now be found by ∫ 0 5 ( d x ⋅ y ) d a ≈ 3 7 . 9 9 4 8 then subtract a quarter of the ellipse π ⋅ 5 ⋅ 3 / 4 to get 2 6 . 2 1 3 8
The perimeter is ∫ 0 5 d x 2 + d y 2 d a ≈ 1 1 . 0 9 4 1
Multiply these by 4 and add them to get S ≈ 1 4 9 . 2 3 1 7 and so ⌊ 1 0 0 0 S ⌋ = 1 4 9 2 3 1
Both the quantities (area of the band and arc length of the outer curve) can be calculated by considering a small length d s on the ellipse as shown below-
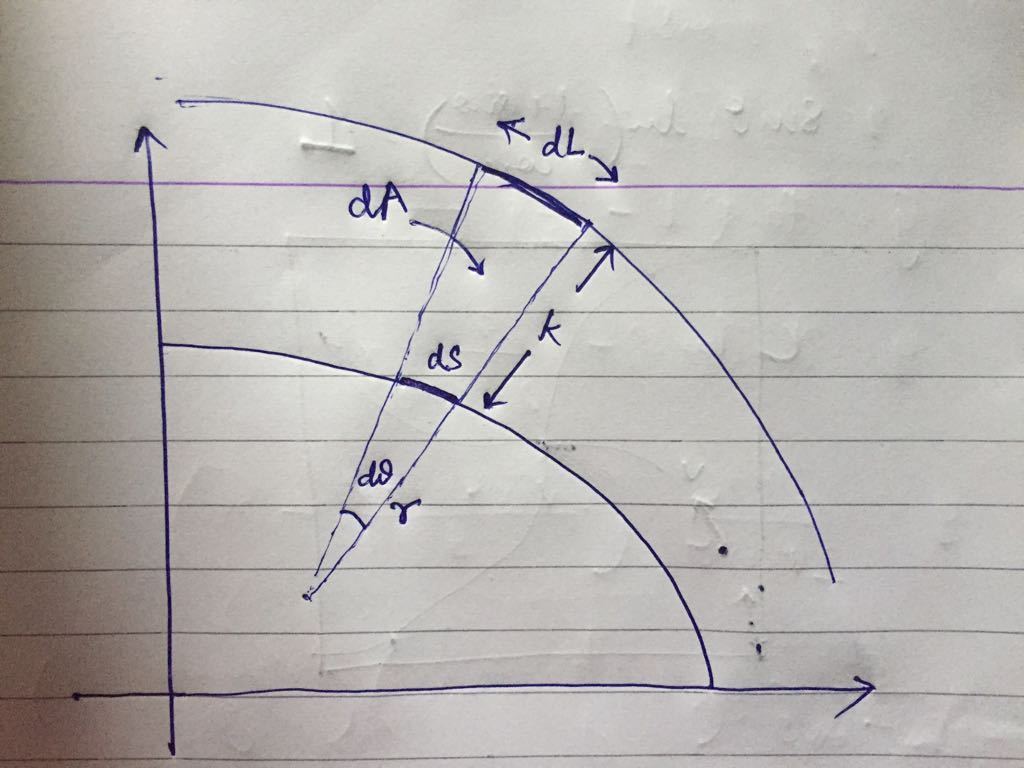
From the above image we can write down following equations-
d s = 1 + y ′ 2 d x
r ∗ d θ = d s
r = y ′ ′ ( 1 + y ′ ) 2 3
d A = outer sector - inner sector = 2 ( r + k ) 2 d θ − 2 r 2 d θ = 2 k 2 d θ − k r d θ
d L = ( 1 + k r ) ∗ d s (using similarity of both sectors)
With the help of above equations, we can eliminate d s , r and d θ and express d A and d L just in terms of x. Integrating over one quadrant and using numerical method for the elliptic integral, we can arrive at the answer - 149.231
Taking inner ellipse as (5, 3) and 3 the thickness of the outer lane, we have x and y on the outer boundary as a function of angle 't' from x axis:
x(t)= 5cos(t)+9cos(t)/√f(t),
y(t)= 3sin(t) +15sin(t)/√f(t), where,
f(t)=(25cos(t)^2+9sin(t)^2)
Integrating by WolframAlpha a simplified expression of y(t){dx(t)/dt} dt from 0 to π/2 gives area as 37.99948. Subtracting 15π/4 and multiplying by 4 gives area of the outer lane of width 3 as 104.85533.
Similarly, integrating by WolframAlpha a simplified expression of √{(dx/dt)^2 + (dy/dt)^2}dt from 0 to π/2 and multiplying by 4 gives perimeter of the external boundary as 44.37655.
Sum of boundary area and perimeter is 104.85533+44.37655=149.23188, and Answer=149231.
The area in question can be divided up into little rectangles and little triangles (all perpendicular to the ellipse) as shown.
Because the ellipse makes a full rotation, all the little triangles will add together to make a circle with radius 3. All the little rectangles will add together to make a rectangle with height 3 and length k where k is the perimeter of the original ellipse. We can see that the total area of the shape in question is 9 π + 3 k and the total perimeter is 6 π + k . Now all we have to do is find k . If a short line segment has horizontal width d x and slope m , the line segment length will be 1 + m 2 d x . This means that k will be equal to 2 ∫ − 5 5 1 + f ′ 2 d x where f ( x ) is the function of the ellipse. We can use an integral calculator to calculate k = 2 5 . 5 2 6 9 9 and Perimeter+Area = 4 k + 1 5 π = 1 4 9 . 2 3 1