An Odd Ratio
1 + 3 + 5 + 7 + ⋯ + 9 9 9 9 9 1 0 0 0 0 1 + 1 0 0 0 0 3 + 1 0 0 0 0 5 + ⋯ + 1 9 9 9 9 9 = ?
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
65 solutions
Moderator note:
Good approach of recognizing that the number of terms cancel out, and so we don't have to perform the multiplication.
100001+199999=100003+199997=......=300000 & 1+99999=3+99997=......=100000 ANS=(300000 multiple 50)/(100000 multiple 50)=3
Log in to reply
I love the simplicity of this solution
If I am not mistaken it should be ((300000 49)+150000)/((100000 49)+50000)= (300000 49.5)/(100000 49.5)=3 because the number in the middle of each series can't be paired...
Log in to reply
when one knows the formula used the result is relatively straightforward. But do you assume this formula is one we innately know OR did I miss something in any of the previous quizzes or courses?
use the formula
An=a + (n-1)d ; where An is the nth term, a is the
first term and d is the common difference
An=199999
a=100001
d=2
substitute the value to the formula
An=a + (n-1)d
199999=100001+(n-1)2
199999=100001+2n-2
199999-100001+2=2n
2n=100000
thus n=50000
Log in to reply
Good Calculation work goin on there Well Done Ma.Lourdes Rogales
I also did it the longer way by calculating n first
Log in to reply
The only problem is that it cannot be 28 percent because it does not work out right because there is not a precise details there and not really much calculation gonna happen anyway.
how is n=5000 here??
Log in to reply
nth term is 199999, a=100001 d=2 so; nth term=a+(n-1)d 199999=100001+(n-1)2 199999-100001+2=2n 99998+2=2n n=50000; hence
Log in to reply
HOW IS D =2??
Log in to reply
@Balkrishna Bhatt – d is the difference btw consecutive terms in this case (3-1),(5-3) and so on its an arithmaticprogression
@Balkrishna Bhatt – d=2 ; a2-a1 =d substituting the numbers into the formula therefore 100003 - 100001 = 2 or 3-1 = 2 because 2 is the common difference
@Balkrishna Bhatt – it was so simple bro
by using an=a1+(n-1)d
These are odd numbers. 1,3,7,...99999. one number is skipped every time. total number will be 50000
i have published my solution kindly see that.
You should also include a way to figure out the term n. Use the equation a + ( n-1 ) * d = l, where a, l, n, and d are the first term, last term, number of terms, and the difference between each term respectively.
Sorry, I must have been talking to myself then. To find out the number of terms, n, we usually assign the i t h term of odd number of the nominator as 1 0 0 0 0 0 + 2 i + 1 and that of the denominator as 2 i + 1 , so that when i = 0 , 1 , 2 , . . . 4 9 9 9 9 , the nominator terms are 1 0 0 0 0 1 , 1 0 0 0 0 3 , 1 0 0 0 0 5 , . . . 1 9 9 9 9 9 and the denominator terms, 1 , 3 , 5 , . . . 9 9 9 9 9 . Since the first term starts with an i = 0 , 0 to 4 9 9 9 9 is 5 0 0 0 0 terms. The first term is 0 + 1 = 1 s t , the last term is 4 9 9 9 9 + 1 = 5 0 0 0 0 t h term.
The equation S = 2 n ( a + l ) is analogous to finding area of a trapezium. For example you want to find the sum S = 4 + 5 + 6 + 7 + 8 = 3 0 , it is the same as finding the average 2 a + l = 2 4 + 8 = 6 and then multiplied it by the number of terms n = 5 and 6 × 5 = 3 0 . Therefore the formula S = 2 n ( a + l ) . Please note that if the series starts with 1 and ends with n the formula becomes S = 2 n ( n + 1 ) which you should be familiar with.
for your kind info u need not calculate n here since it is an odd ap the n in numerator is gng to be the same as that of denominator and hence cancels out...so it is enough if find (a+l) for both numerator and denominator
good thinking and very simple to understand thanks
We can rewrite the Numerator as 100000 * n + Denominator ( S) . Also, S = n/2 * (1 + 99999) = n * 50000. So, fraction = 2 + 1 = 3
why isn't the following right? :
[100000(1+3+5+...+99999)]/ (1+3+5+...+99999) 100000c/c = 100000?
Log in to reply
Well, guys, why this solution is false?
The upper term isn't [100000(1+3+5+...+99999)], it's [100000(1+(1+3+5+...+99999))]. Otherwise the first term would be 100000, and the final term would be 9999900000.
It's 49999 additions of 100000 to 49999 individual terms, not multiplication of 49999 individual terms by 100000.
I hope one of those statements clarifies it.
wow!!! ,so simple
There's a nice shortcut... First n odd numbers is n^2 and we have 50 000 terms, so the denominator equals 50 000^2
We can split the numerator to
(100 000 (50 000)) + (1+3+5+...+99 999)
Hence the original simplifies to
((100 000 × 50 000) + (50 0000)^2) ÷ (50 0000)^2
=(100 0000 + 50 000) ÷ 50 0000 =150 0000 ÷ 50 000 = 3
Good, I used the same method
Why it is n=50000/2 here. Actually, when I tackle these kind of prolem I just eliminate the two 2 n from denominator and numerator
what is the value of n
I SOLVED like this solution
right. How's n= 5000
Log in to reply
It's not, it's 50,000.
Log in to reply
no!!!!, n=49,999...
Log in to reply
@Karan Kishore – No, n does equal 50,000.
Take the first term of the sequence in the denominator or numerator, add it to any of the other terms in that sequence, then divide by the difference between successive terms. Example using the denominator:
n = 2 1 + 9 = 5
How many terms are there in the denominator up to and including 9? 1, 3, 5, 7, 9. Five terms. Try it with 3, 5, 7, 11, or any other number in that sequence that you'd like if you don't believe me.
n = 2 1 + 9 9 , 9 9 9 = 2 1 0 0 , 0 0 0 = 5 0 , 0 0 0
See my reply on Oct 3
Wrong solution. If you take 100000 as a common from the numerator, you will have 100000 multiplied by the denominator, so the solution is 100000.
Log in to reply
You cannot take 100000 common from numerator.
where did you get n=50000
I used n = 99999 and it gave me correct answer, can you elaborate more how you got 50000 please, Thank you !
Reason for 99999 is (199999 - 100001) + 1 = 99999
Log in to reply
Because of the way the expression is formed, it doesn't matter what you use for n (in this case). The n term exists in the numerator and denominator in the same form, so it is cancelled out.
if the terms were 1+2+3+...+99999, then there would be 99999 terms. Because the terms are 1+3+5+...+99999, you're cutting out 49999 of the possible terms, i.e., all of the even numbers, leaving 50000 terms for the calculation.
how do you manage to work that out because i am a top set maths teacher at London Community Upper School and even my top set maths students cannot work that out. Because it is to hard for them and even for me because i have done those sort of questions anyway.
Log in to reply
Sorry, I didn't notice your question earlier. We only need to sum of AP, specially when the common difference is not 1 , is given by S = 2 n ( a + 1 ) . The rest is just computation.
Isn't the numerator 100000 ( 1+3+...+99999) ?
Log in to reply
No. That would be 100000 +300000 +...+ 9999900000 and not 100001 + 100003 + ... + 199999
The last four nines in the numerator are missing in the challenge picture. It shows "100001 + 100003 + 100005 + ... + 19". Very confusing, please correct.
Log in to reply
There is no problem with my screen. You can scroll right with the bar at the bottom.
Log in to reply
There's no scrollbar on mobiles. There is no indication that part of the term is cropped at all, except that it doesn't appear to make sense. Anyway, seems to be a problem with the site, not with the question. Thanks for investigating.
Log in to reply
@Vincent Gabriel – There is scroll bar on my mobile. Check your app. I continued my streak in China using a mobile.
NICE SOLUTION
How can we know that n = 50000? In the fast way
Log in to reply
The way that I explained is the fastest I know. For example, for the series 1 , 3 , 5 , 7 , . . . , if we assign 1 = 2 ( 1 ) − 1 , 3 = 2 ( 2 ) − 1 , 5 = 2 ( 3 ) − 1 ... 9 9 9 9 9 = 2 ( 5 0 0 0 0 ) − 1 . So, we can see that for 1 , n = 1 ; 3 , n = 2 ; 5 , n = 3 ; ... 9 9 9 9 9 , n = 5 0 0 0 0 .
1 + 3 + ⋯ + ( 2 n − 1 ) = n 2 If the last term is 99999 then 2 n − 1 = 9 9 9 9 9 ⇒ n = 5 0 0 0 0 .
Haha solved it the same way (+1)
Can we take 100000 common and cancel out the number
Log in to reply
Yes, of course, you can. I was only showing one way of solving the problem.
Those upvotes though
But we should find the number of terms by using general term of an A.P. which is a+(n-1)d. The number of terms will then come 50000
Log in to reply
Yes, the number of terms is 50000 as used in my solution.
100000 (1+3+5...99999)÷(1+3+5+7+.....99999)=100000
Is it wrong
Log in to reply
1 0 0 0 0 0 ( 1 + 3 + 5 + . . . + 9 9 9 9 9 ) = 1 0 0 0 0 0 + 3 0 0 0 0 0 + 5 0 0 0 0 0 + . . . + 9 9 9 9 9 0 0 0 0 0 = 1 0 0 0 0 1 + 1 0 0 0 0 3 + 1 0 0 0 0 5 + . . . + 1 9 9 9 9 9 .
The numerator you've created is 1 0 0 0 0 0 + 3 0 0 0 0 0 + . . . + 9 9 9 9 9 0 0 0 0 0 not 1 0 0 0 0 1 + 1 0 0 0 0 3 + . . . + 1 9 9 9 9 9
You need 1 + 3 + . . . + 9 9 9 9 9 5 0 0 0 0 ( 1 0 0 0 0 0 ) + ( 1 + 3 + . . . + 9 9 9 9 9 )
Answer is 100000
Can anyone explain why n is divided by 2 (in the equation n/2(n+l) )
also, is there a reason for the specific letters, or is the use of S, n, a, and l simply a matter of choice?
same what i did
where did you get 50000????
how is n=50000 here???????????????
It's wrong
The numerator can be written as (100000+1)+(100000+3)+(100000+5)+......(100000+99999)
The number of 100000's are 99999+1/2=50000 (Nth term of a odd series is given by an+1/2)
That gives us 50000X100000+(1+3+5+....+99999)/(1+3+5+....+99999)
So the answer is 50000X100000
Log in to reply
1 + 3 + 5 + . . . + 9 9 9 9 9 1 0 0 0 0 0 × 5 0 0 0 0 + ( 1 + 3 + 5 + . . . + 9 9 9 9 9 ) = 2 , 5 0 0 , 0 0 0 , 0 0 0 5 , 0 0 0 , 0 0 0 , 0 0 0 + 2 , 5 0 0 , 0 0 0 , 0 0 0 = 3
You can try with 1 + 3 + 5 + . . . + 9 9 1 0 1 + 1 0 3 + 1 0 5 + . . . + 1 9 9 and you should get the same answer.
Log in to reply
sorry! I made a mistake. it was a little confusing to write it on here. my bad
Could you explain me why the the number of terms n are 50000?
Log in to reply
I have actually explained it just before your post. Anyway, I cut-and-paste it here.
To find out the number of terms, n , we usually assign the i t h term of odd number of the nominator as 1 0 0 0 0 0 + 2 i + 1 and that of the denominator as 2 i + 1 , so that when i = 0 , 1 , 2 , . . . 4 9 9 9 9 , the nominator terms are 1 0 0 0 0 1 , 1 0 0 0 0 3 , 1 0 0 0 0 5 , . . . 1 9 9 9 9 9 and the denominator terms, 1 , 3 , 5 , . . . 9 9 9 9 9 . Since the first term starts with an i = 0 , 0 to 4 9 9 9 9 is 5 0 0 0 0 terms. The first term is 0 + 1 = 1 s t , the last term is 4 9 9 9 9 + 1 = 5 0 0 0 0 t h term.
Notice that we can form 2 5 0 0 0 pairs of numbers whose sum is 1 0 0 0 0 0 in the denominator: ( 1 + 9 9 9 9 9 ) , ( 3 + 9 9 9 9 7 ) , ( 5 + 9 9 9 9 5 ) etc.. And in the numerator we can do the same thing, but 1 0 0 0 0 0 is added to each of the 5 0 0 0 0 terms. So we have:
1 + 3 + 5 + 7 + 9 + 1 1 + … + 9 9 9 9 9 1 0 0 0 0 1 + 1 0 0 0 0 3 + 1 0 0 0 0 5 + … + 1 9 9 9 9 9
= 2 5 0 0 0 × 1 0 0 0 0 0 2 5 0 0 0 × 1 0 0 0 0 0 + 5 0 0 0 0 × 1 0 0 0 0 0
= 2 5 0 0 0 × 1 0 0 0 0 0 7 5 0 0 0 × 1 0 0 0 0 0
= 2 5 0 0 0 7 5 0 0 0 = 2 5 7 5 = 3
best technique for anyone who cant remember the formula if S = (n/2)*(1st + last) =)
This was easy really just you need a new perspective to see the math
If we define n to be the number of terms within the divisor. Then if we look at n t h term, we have: 1 + 3 + 5 + . . . + ( 2 n − 3 ) + ( 2 n − 1 ) ( 2 n + 1 ) + ( 2 n + 3 ) + . . . + ( 4 n − 3 ) + ( 4 n − 1 ) By inputting the values n = 1 , n = 2 and n = 3 , we achieve the following sequences: n = D i v i s o r : 1 1 2 4 3 9 Clearly we can see that for the divisor, the n t h term equals n 2
Repeating the process for the dividend, we get: n = D i v i d e n d : 1 3 2 1 2 3 2 7 Then, by finding the n t h term of the sequence using a method of your liking, you should end up with an n t h term of 3 n 2
Now, by placing our two n t h term values back into the original equation, we have: n 2 3 n 2 By simplifying this equation we end up with an answer of 3
Note: The equation shown is for n = 5 0 0 0 0 , which would still result to 3.
Very nice solution different from others
Fabulous solution by using basic number theory.
Log in to reply
Thank you! I try to use n t h terms wherever I can!
Inspiring.
The first solution is amazing
the given expression can be written as
1 + 3 + 5 . . . . . + 9 9 9 9 9 ( 1 0 0 0 0 0 + 1 ) + ( 1 0 0 0 0 0 + 3 ) + ( 1 0 0 0 0 0 + 5 ) + . . . . . ( 1 0 0 0 0 0 + 9 9 9 9 9 )
now separating 1 0 0 0 0 0 we get the expression as
1 + 3 + 5 . . . + 9 9 9 9 9 ( 1 0 0 0 0 0 × 5 0 0 0 0 ) + ( 1 + 3 + 5 . . . . + 9 9 9 9 9 ) ( ∵ n o . o f t e r m s a r e 5 0 0 0 0 )
now separating the fraction as 1 + 3 + 5 . . . + 9 9 9 9 9 ( 1 0 0 0 0 0 × 5 0 0 0 0 ) + 1 + 3 + 5 . . . + 9 9 9 9 9 ( 1 + 3 + 5 . . . . + 9 9 9 9 9 )
we get 2 5 0 0 0 0 ( 1 + 9 9 9 9 9 ) 1 0 0 0 0 0 × 5 0 0 0 0 + 1
finally the answer is 1 + 2 = 3
I did same way
I hope this explanation will be easy to understand. First off , we can see that 100,001+199,999=300,000. Similarly 100,003+199,997=300,000 and so on.This is the same with the denimenator.Since the number of terms being added in the numerator and the denominator are the same and give the same 300,000/100,000=3,3 is the answer.
Excellent explanation - this is precisely how I arrived at the answer.
Why are all the other answers so complicated when the solution is so simple?
There's actually a simple solution to it. The denominator is the sum of the first x odd numbers. The numerator is the sum of the next x odd numbers, or the sum of the first 2x, minus the sum of the first x. The result is x 2 for the denominator and ( 2 x ) 2 − x 2 , 4 x 2 − x 2 , or 3 x 2 for the numerator.
Thus, as long as the number of terms is the same, and the numerator picks up where the denominator left off, the answer is always 3.
This is simply the best answer.
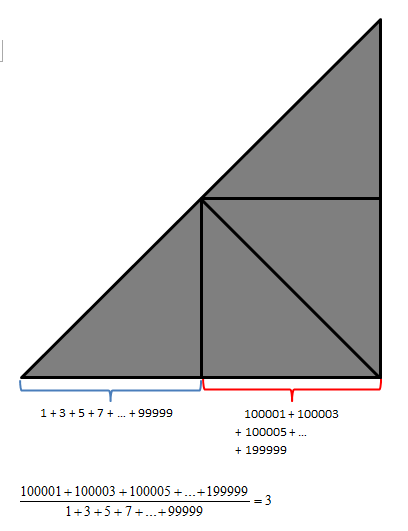
100001 + 100003 + 100005 + ... + 199999
= (100000+1) + (100000+3) + (100000+5) + ... + (100000+99999)
= (100000 + 100000 + 100000 + ... + 100000) + (1 + 3 + 5 + 7 + ... + 99999)
= (1+99999) + (2+99998) + (3+100000) + ... + (99999+1) + (1 + 3 + 5 + 7 + ... + 99999)
= 3 × (1 + 3 + 5 + 7 + ... + 99999)
1 + 3 + 5 + 7 + . . . + n = ( 2 n + 1 ) 2 , so the denominator sums to ( 2 9 9 9 9 9 + 1 ) 2 = 5 0 0 0 0 2 .
Whereas, for the numerator, we have ( 2 1 9 9 9 9 9 + 1 ) 2 − 5 0 0 0 0 2 = 1 0 0 0 0 0 2 − 5 0 0 0 0 2 = 3 × 5 0 0 0 0 2 .
Good and nice solution
Beautiful solution
short cut and nice solution
1 + 3 + 5 + 7 + 9 + 1 1 + … + 9 9 9 9 9 1 0 0 0 0 1 + 1 0 0 0 0 3 + 1 0 0 0 0 5 + … + 1 9 9 9 9 9
= 1 + 3 + 5 + 7 + 9 + 1 1 + … + 9 9 9 9 9 1 0 0 0 0 0 + 1 + 1 0 0 0 0 0 + 3 + 1 0 0 0 0 0 + 5 + … + 1 0 0 0 0 0 + 9 9 9 9 9
= 1 + 3 + 5 + 7 + 9 + 1 1 + … + 9 9 9 9 9 ( 1 0 0 0 0 0 + 1 0 0 0 0 0 + 1 0 0 0 0 0 + … + 1 0 0 0 0 0 ) + ( 1 + 3 + 5 + … + 9 9 9 9 9 )
= 1 + 3 + 5 + 7 + 9 + 1 1 + … + 9 9 9 9 9 ( n i × 1 0 0 0 0 0 ) + ( 1 + 3 + 5 + … + 9 9 9 9 9 )
= 1 + 3 + 5 + … + 9 9 9 9 9 n i × 1 0 0 0 0 0 + 1
no of integers n i = 2 9 9 9 9 9 − 1 + 1 = 5 0 0 0 0
Sum of all odd integers of n (odd) numbers = 4 n − 1 ∗ ( n + 1 ) + 2 n + 1
= 4 n 2 − 1 + 2 ( n + 1 )
= 4 9 9 9 9 9 2 − 1 + 2 ( 9 9 9 9 9 + 1 ) = 2 5 0 0 0 0 0 0 0 0 = 2 . 5 × 1 0 9
= 2 . 5 × 1 0 9 5 × 1 0 9 + 1 = 2 + 1 = 3
My solution goes like this: From the given, it can be seen that there are an equal number of terms in the numerator and the denoninator. We denote this as y. And there is a constant sum for each pair (1, 99999), (3, 99997), (5, 99995), ... which is equal to 100000. We denote x = 100000. The denominator can then be simplified to xy/2. This follows that the numerator be equal to xy + xy/2. There is one 100000 for each term, and the sum xy/2. Therefore, the expression can be simplified to (xy + xy/2)/(xy/2). Or simply 1.5/.5 = 3.
well their common difference is 2 (both the numerator and denominator) and the difference from the first and last term (for both the numerator and the denominator) is the same: 99998. therefore, the number of terms for both numerator and denominator is the same; and so, just get the sum of the first and last terms of the numerator and divide it by the first and last terms of the denominator. There is no need for solving the exact values of the numerator and denominator since the number of terms are the same. You will just end up cancelling them out if you did.
Equation: (100001+199999) / (1+99999) = 3
Take 100001=100000+1 and so on till 199999.We get 100000*50000+(50000)^2/50000^.This solving we get 3
Let a = 1 0 0 0 0 0 . The expression now becomes:
1 + 3 + 5 + 7 + ⋯ + 9 9 9 9 9 ( a + 1 ) + ( a + 3 ) + ( a + 5 ) + ⋯ + ( a + 9 9 9 9 9 ) .
We should note now, that between 1 and 9 9 9 9 9 there are 5 0 0 0 0 odd numbers (extremes included). Thus, we have:
1 + 3 + 5 + ⋯ + 9 9 9 9 9 5 0 0 0 0 a + 1 + 3 + 5 + ⋯ + 9 9 9 9 9 .
Since the sum of the first n odd numbers is n 2 , it follows that 1 + 3 + 5 + ⋯ + 9 9 9 9 9 = ( 5 0 0 0 0 ) 2 .
Now our expression becomes:
( 5 0 0 0 0 ) 2 5 0 0 0 0 a + ( 5 0 0 0 0 ) 2 .
Factor the numerator by 50000:
( 5 0 0 0 0 ) 2 5 0 0 0 0 ( a + 5 0 0 0 0 ) = 5 0 0 0 0 a + 5 0 0 0 0 .
Substitute back a :
5 0 0 0 0 1 0 0 0 0 0 + 5 0 0 0 0 = 5 0 0 0 0 1 5 0 0 0 0 = 3 .
x = 1 + 3 + 5 + 7 + . . . + 9 9 9 9 9 1 0 0 0 0 1 + 1 0 0 0 0 3 + 1 0 0 0 0 5 + . . . + 1 9 9 9 9 9
Denominator is sum of odd numbers, so let's work that out first:
n = 0 ∑ N ( 2 n + 1 )
n = 0 ∑ N 2 n + n = 0 ∑ N 1
2 n = 0 ∑ N n + ( N + 1 )
2 2 N ( N + 1 ) + ( N + 1 )
N ( N + 1 ) + ( N + 1 )
( N + 1 ) ( N + 1 )
( N + 1 ) 2
Cool! So the denominator is just ( N + 1 ) 2 . We'll work out the value of N later.
Now, the numerator is a similar sum except the value 1 0 0 0 0 0 is added to each term:
n = 0 ∑ N ( 2 n + 1 + 1 0 0 0 0 0 )
n = 0 ∑ N ( 2 n + 1 ) + n = 0 ∑ N 1 0 0 0 0 0
( N + 1 ) 2 + ( N + 1 ) ( 1 0 0 0 0 0 )
( N + 1 ) ( ( N + 1 ) + 1 0 0 0 0 0 )
So the result of the whole series is just:
x = \frac{ \cancel{(N+1)}((N+1) + 100000)}{(N+1)^\cancel{2}}
x = ( N + 1 ) ( N + 1 ) + 1 0 0 0 0 0
Now we need to work out the value of N . The maximum odd number we compute is 9 9 9 9 9 , so:
2 N + 1 = 9 9 9 9 9
2 N = 9 9 9 9 8
N = 4 9 9 9 9
∴ x = ( N + 1 ) ( N + 1 ) + 1 0 0 0 0 0 = 5 0 0 0 0 5 0 0 0 0 + 1 0 0 0 0 0 = 3
Writing large numbers is error prone so we can let a = 1 0 0 0 0 0 Using formula S = 2 n ( a + l ) on both numerator and denominator.
= 2 1 ( ( 1 ) + ( a − 1 ) ) ( a − 1 ) 2 1 ( ( a + 1 ) + ( 2 a − 1 ) ) ( a − 1 )
simplify:
= a 3 a
= 3
2 5 0 0 0 ( 1 + 9 9 9 9 9 ) 2 5 0 0 0 ( 1 0 0 0 0 1 + 1 9 9 9 9 9 ) = 1 0 0 0 0 0 ) 3 0 0 0 0 0 = 3
the rule is =n(n+1)/2
so,100001+...................199999=n(n+1)/2=1.5 x 10^10
and 1+3+...........99999=n(n+1)/2=5 x 10^9
so,1.5 x 10^10/5 x 10^9=3
extracting 100000 from all of the terms in the numerator, and finding the number of terms , you can get (50000)(100000) + 1+3+5+7...99999. You might know that the sum of all odd numbers from 1 to n is ((n+1)/2)^2, applying that also to all of the original terms of the denominator, you get (50000)(100000) +(50000)(50000)/ (50000)(50000), canceling out 50000 from the numerator and denominator, after you combined (50000)(100000) and (50000)(50000) from the numerator, you get 150000/50000 and you get 3
Sum of odd numbers is n². So, between 1 .. 99999 has fifty thousands numbers, thus n² = 50000² = 2500000000.
100001 + 100003 + 100005 = (100000+1) + (100000+3) ... (100000+99999) (100000 * 50000) + (1+3+5 .... + 99999) = (100000 * 50000) + (50000²)
Thus (100000 * 50000) + (50000²) / (50000²) = 3
Pardon for my poor english :)
We can separate the big numbers in the numerator into 100000 +an odd number from 1 to 99999. We need to solve for the amount of positive odd numbers up to 99999. We can do this by using the generating function for odd numbers:
a n = 2 n − 1 Solving for 99999 as an odd number, we get the following:
9 9 9 9 9 = 2 n − 1
1 0 0 0 0 0 = 2 n
5 0 0 0 0 = n Now all we need to do is sum the top expression and the bottom expression as follows: x = ∑ n = 1 5 0 0 0 0 2 n − 1 1 0 0 0 0 0 ∗ 5 0 0 0 0 + ∑ n = 1 5 0 0 0 0 2 n − 1
Plugging this into a calculator with a computer algebra system, we get x=3.
The denominator and numerator each have ( 9 9 9 9 9 − 1 ) ÷ 2 + 1 = 5 0 0 0 0 numbers. Gauss Theorem : 1 + 3 + 5 + 7 + ⋯ + 9 9 9 9 9 1 0 0 0 0 1 + 1 0 0 0 0 3 + 1 0 0 0 0 5 + ⋯ + 1 9 9 9 9 9 = ( 1 + 9 9 9 9 9 ) × 2 5 0 0 0 0 ( 1 0 0 0 0 1 + 1 9 9 9 9 9 ) × 2 5 0 0 0 0 = 1 0 0 0 0 0 3 0 0 0 0 0 = 3
I used our good friend Gauss. Gauss' trick says that if there are an even number of terms, you can use this (for example) (I will use consecutive numbers starting from 1, other sequences work the same way): 1 + 2 + 3 + ... + n-2 + n-1 + n = ( 2 n * (n + 1)) Then, we can apply it to the numerator (sum 300000 and 25000 terms), and the denominator (sum 100000 and also 25000 terms). We have the fraction 2 5 0 0 0 ∗ 1 0 0 0 0 0 2 5 0 0 0 ∗ 3 0 0 0 0 0 , a very annoying way of writing 3 (divide the 25000s and 100000 off of both).
I got a simple method for the question. Add up the first number and the last number in the numerator, and then add up the first and the last number in the denominator. Divide the larger number by the smaller number. That's the correct answer!
set 1 + 3 + 5 + 7 + . . . + 9 9 9 9 9 = a , the numerator becomes 1 0 0 0 0 0 ∗ ( 9 9 9 9 9 − 1 ) / 2 + a , (there are ( 9 9 9 9 9 − 1 ) / 2 100000s therefore the expression can become 1 0 0 0 0 0 ∗ ( 9 9 9 9 9 − 1 ) / 2 / a + 1 ; a=(first term + last term)*(number of terms)/2= 1 0 0 0 0 0 ∗ ( 9 9 9 9 9 − 1 ) / 2 / 2 so the expression becomes 2+1=3
Let's solve it in a very short time using the trick that the sum of the first n odd is n². Using this, The numerator is ((199999+1)/2)²-((100001-1)/2)² =(2 50000)²-50000² =3 50000². The denominator, ((99999+1)/2)²=50000 Solution is (3*50000²)/50000²=3
5 0 0 0 0 2 ( 1 0 5 × 5 0 0 0 0 ) + 5 0 0 0 0 2 = 5 0 0 0 0 2 5 0 0 0 0 2 ( 5 0 0 0 0 1 0 5 + 1 ) = 5 0 0 0 0 1 0 5 + 1 = 3
1 + 3 + 5 + . . . + 9 9 , 9 9 9 ( 1 0 0 , 0 0 1 + 1 0 0 , 0 0 3 + 1 0 0 , 0 0 5 + . . . + 1 9 9 , 9 9 9 ) = 1 + 3 + 5 + . . . + 9 9 , 9 9 9 ( 1 0 0 , 0 0 0 + 1 0 0 , 0 0 0 + 1 0 0 , 0 0 0 + . . . + 1 0 0 , 0 0 0 ) + ( 1 + 3 + 5 + . . . + 9 9 , 9 9 9 ) W e n o w t h a t 1 + 3 + 5 + . . . + 9 9 , 9 9 9 i s t h e s u m o f a s e q u e n c e o f n t e r m s w h e r e t h e n t h t e r m i s 2 n − 1 . W e w a n t t o k n o w t h e n u m b e r o f t e r m s i n o r d e r t o s i m p l i f y o u r c a l c u l a t i o n . I f t h e l a s t t e r m o f t h e s e q u e n c e i s 9 9 , 9 9 9 = 2 n − 1 → n = 5 0 , 0 0 0 S o 1 + 3 + 5 + . . . + 9 9 , 9 9 9 [ ( 1 0 0 , 0 0 0 + 1 0 0 , 0 0 0 + 1 0 0 , 0 0 0 + . . . + 1 0 0 , 0 0 0 ) + ( 1 + 3 + 5 + . . . + 9 9 , 9 9 9 ) ] = ∑ n = 1 5 0 , 0 0 0 2 n − 1 1 0 0 , 0 0 0 ∗ 5 0 , 0 0 0 + ∑ n = 1 5 0 , 0 0 0 2 n − 1 = ∑ n = 1 5 0 , 0 0 0 2 n − 1 1 0 0 , 0 0 0 ∗ 5 0 , 0 0 0 + ∑ n = 1 5 0 , 0 0 0 2 n − 1 ∑ n = 1 5 0 , 0 0 0 2 n − 1 = ∑ n = 1 5 0 , 0 0 0 2 n − ∑ n = 1 5 0 , 0 0 0 1 5 , 0 0 0 , 0 0 0 , 0 0 0 + 1 = 2 ∑ n = 1 5 0 , 0 0 0 n − ∑ n = 1 5 0 , 0 0 0 1 5 , 0 0 0 , 0 0 0 , 0 0 0 + 1 = 2 2 ( 5 0 , 0 0 0 ∗ ( 5 0 , 0 0 0 + 1 ) − 5 0 , 0 0 0 5 , 0 0 0 , 0 0 0 , 0 0 0 + 1 = ( 5 0 , 0 0 0 ∗ 5 0 , 0 0 1 ) − 5 0 , 0 0 0 5 , 0 0 0 , 0 0 0 , 0 0 0 + 1 = 5 0 , 0 0 0 ∗ 5 0 , 0 0 1 − 5 0 , 0 0 0 5 , 0 0 0 , 0 0 0 , 0 0 0 + 1 = 2 , 5 0 0 , 0 0 0 , 0 0 0 5 , 0 0 0 , 0 0 0 , 0 0 0 + 1 = 2 + 1 = 3
There are 5000 terms in both the numerator and the denominator. Each of these pairs of terms can be added: Denominator: 1 + 99999 = 10000 2 + 99998 = 10000 3 + 99997 = 10000 ... ... 5001 + 4999 = 10000, Therefore the denominator equals 5000 x 10000 = 50,000,000 By parallel reasoning, the numerator reduces to 150,000,000 Therefore the fraction itself evaluates to 3.
This may also be solved by multiple cancellation.
The sum of n sequential terms is 2 n ( f + l ) , where f and l are the first and last items respectively.
This gives us: 2 n ( 1 + 1 9 9 9 9 9 ) 2 n ( 1 0 0 0 0 1 + 1 9 9 9 9 9 ) .
The 2 n cancels out, giving us: 1 + 1 9 9 9 9 9 1 0 0 0 0 1 + 1 9 9 9 9 9 = 1 0 0 0 0 0 3 0 0 0 0 0 = 3 .
3 is the answer.
Sum of first n odd integers is n 2 . So our denominator is 5 0 0 0 2 .
Numerator has 5 0 0 0 terms, each of which is 1 0 0 0 0 + i where the i 's range through the first 5 0 0 0 odd integers. So the numerator is 1 0 0 0 0 ⋅ 5 0 0 0 + 5 0 0 0 2 = 3 ∗ 5 0 0 0 2 . Hence the overall value is 5 0 0 0 2 3 ∗ 5 0 0 0 2 = 3 .
1) Notice that the sum 1 + 2 + 3 + ⋯ + 9 9 9 9 9 contains 2 1 + 9 9 9 9 9 = 5 0 0 0 0 terms.
2) Thus both the denominator and the numerator consists of n = 5 0 0 0 0 terms. The sum of the first n odd integers are n 2 , and thus we have
1 + 2 + ⋯ + 9 9 9 9 9 1 0 0 0 0 1 + 1 0 0 0 0 2 + ⋯ + 1 9 9 9 9 9 = 5 0 0 0 0 2 5 0 0 0 0 ⋅ 1 0 0 0 0 0 + 5 0 0 0 0 2
3) Carrying out the divison term-wise gives us 5 0 0 0 0 1 0 0 0 0 0 + 1 = 2 + 1 = 3 .
Sum of n consecutive odd numbers(starting from 1) give n^2 eg. 1+3=4=2^2 hence we can denote S=1+3+5.......99999 as 50000^2=25×10^8 so in numerator it is written (5×10^9)+S and denominator is S so by putting value of S it simplifies to 3
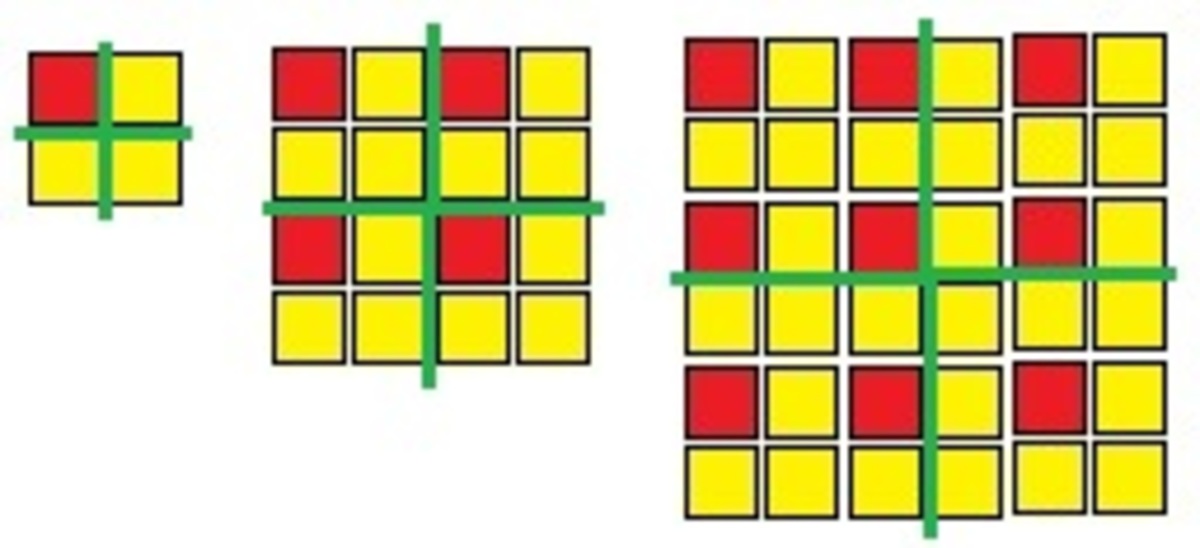 From the AP 1,3,5,7,9,11,13,15,17,19,21,..., start making ratios:
From the AP 1,3,5,7,9,11,13,15,17,19,21,..., start making ratios:
3/1=3; 1+3=4 see the little square size 2.
Increasing the denominator and numerator by one results in even sizes of squares.
And is always possible 2 green lines to divide every new square in 4 equal squares.
(5+7)/(1+3)=12/4=3; 4+12=16 see the larger square size 4.
And we can see every new square has 3 parts denominator and one part numerator.
(7+9+11)/(1+3+5)=27/9=3; 9+27=36 see the largest square size 6.
(9+11+13+15)/(1+3+5+7)=48/16=3; 16+48=64 and so on . . .size 8.
This way the ratio of 3 never changes.
. . . . . . . . . . . . . . . . . . . . . . . . . . . 75/25=3; 25+75=100 . . . size 10.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108/36=3; 36+108=144 . . . size 12.
. . . . . . . . . . . . . . . . . . . size 1000, size 1000000, size 1000000000 . . .
Multiply both numerator and denominator by 2 to make a copy in reverse order.
Numerator:
1 0 0 0 0 1 + 1 0 0 0 0 3 + 1 0 0 0 0 5 + … + 1 9 9 9 9 5 + 1 9 9 9 9 7 + 1 9 9 9 9 9 1 9 9 9 9 9 + 1 9 9 9 9 7 + 1 9 9 9 9 5 + … + 1 0 0 0 0 5 + 1 0 0 0 0 3 + 1 0 0 0 0 1
3 0 0 0 0 0 + 3 0 0 0 0 0 + 3 0 0 0 0 0 + … + 3 0 0 0 0 0 + 3 0 0 0 0 0 + 3 0 0 0 0 0
Denominator:
0 0 0 0 0 1 + 0 0 0 0 0 3 + 0 0 0 0 0 5 + … + 0 9 9 9 9 5 + 0 9 9 9 9 7 + 0 9 9 9 9 9 0 9 9 9 9 9 + 0 9 9 9 9 7 + 0 9 9 9 9 5 + … + 0 0 0 0 0 5 + 0 0 0 0 0 3 + 0 0 0 0 0 1
1 0 0 0 0 0 + 1 0 0 0 0 0 + 1 0 0 0 0 0 + … + 1 0 0 0 0 0 + 1 0 0 0 0 0 + 1 0 0 0 0 0
There is the same number of terms, so we get
1 0 0 0 0 0 3 0 0 0 0 0 = 3
The numerator and denominator is in the form of arithmetic progression. We need to get the sum of the progression on the numerator then divide it by the sum of the progression on the denominator.
S = n/2(a1 + an)
The answer is 3.
number of terms=50000 both in numerator & denominator Sum of Numerator = 100000 * 50000 + 50000 * 50000 (sum of 50000 odd numbers) = 5k *(1 lac+5k) Sum of Denominator = 5k * 5k (sum of 50000 odd numbers) Thus we have our final answer after cancelling out 5k both in numerator and denominator. Which is - 1,50,000/50,000 = 3
First step is to find out how many terms there are on the numerator and the denominator. It is quite obvious that there are the same number of terms in the numerator and the denominator.
Here, the last term of the numerator is 199999 ( A n ), first term is 100001 ( a ), the common difference between two odd numbers is 2 ( d ) A n = a + ( n − 1 ) d 1 9 9 9 9 9 = 1 0 0 0 0 1 + 2 ( n − 1 ) n = 2 1 9 9 9 9 9 − 1 0 0 0 0 1 + 2 n = 5 0 0 0 0
Now we know,
1 + 3 + 5 + 7 + . . . . . . . . . . + A n = n 2 n t e r m s
So,
1 + 3 + 5 + 7 + . . . + 9 9 9 9 9 = 5 0 0 0 0 2
and,
1 0 0 0 0 1 + 1 0 0 0 0 3 + 1 0 0 0 0 5 + 1 0 0 0 0 7 + . . . . . . . . + 1 9 9 9 9 9 = 5 0 0 0 0 ( 1 0 0 0 0 0 ) + 5 0 0 0 0 2 = 5 0 0 0 0 ( 1 0 0 0 0 0 + 5 0 0 0 0 ) = 5 0 0 0 0 × 1 5 0 0 0 0
Thus we have,
5 0 0 0 0 ( 5 0 0 0 0 ) 5 0 0 0 0 ( 1 5 0 0 0 0 ) = 5 0 0 0 0 1 5 0 0 0 0 = 3
My solution was similar. 1 + 3 + ⋯ + ( 2 n − 1 ) = n 2 1 + 3 + ⋯ + 9 9 9 9 9 = n 2 ⇒ 2 n − 1 = 9 9 9 9 9 ⇒ n = 5 0 0 0 0 similarly 1 + 3 + ⋯ + 1 9 9 9 9 9 = k 2 ⇒ k = 1 0 0 0 0 0 . In the numerator we have 1 0 0 0 0 1 + 1 0 0 0 0 3 + ⋯ + 1 9 9 9 9 9 = ( 1 + 3 + ⋯ + 1 9 9 9 9 9 ) − ( 1 + 3 + ⋯ + 9 9 9 9 9 ) = k 2 − n 2 hence 5 0 0 0 0 2 1 0 0 0 0 0 2 − 5 0 0 0 0 2 = 5 0 0 0 0 2 1 0 0 0 0 0 2 − 1 = ( 5 0 0 0 0 1 0 0 0 0 0 ) 2 − 1 = 2 2 − 1 = 4 − 1 = 3
Firstly: 100001+100003+...+199999 100000N+1+3+...+99999
Thus by breaking it apart between 100000N and 1 and dividing: 100000N/ (1+3+5+7+...+99999) +1 Equation (1)
So for the series expand the last 4 as well as the first 4 1+3+5+7+....+99993+99995+99997+99999
Then first and last sums up, the 2nd and 2nd last sums up etc. So that: 1+99999 + 3+99997 + 5+99995+.. =100000*N/2 Equation (2)
But the series can be shown to be showed by: N + (N-1)= 2N-1 Calculating the number of terms: 99999=2N-1 50000=N
Thus Equation (1) can be expressed as follows: 100000N/(100000*N/2) + 1 Equation (3)
By substituting 50000 into equation 3:
2+1 =3
My solution was this:
1 + 3 + . . . + 9 9 9 9 9 1 0 0 0 0 1 + 1 0 0 0 0 3 + . . . + 1 9 9 9 9 9 = n = 0 ∑ n = k − 1 2 n + 1 1 0 0 0 0 k + n = 0 ∑ n = k − 1 2 n + 1 = n = 0 ∑ n = k − 1 2 n + 1 1 0 0 0 0 0 k + 1
The sum equals:
n = 0 ∑ n = k − 1 2 n + 1 = 2 1 + 2 ( k − 1 ) + 1 k = k 2
And the result is:
k 1 0 0 0 0 0 + 1 = 3
Because k = 2 1 0 0 0 0 0
This is simple AP nothing else
if you reduce this down to 101-199 over 1+3 ... 99 you get n^2+100n/n^2 ==> there are 50 terms between => n = 50..
50^2+100(50)/50^2
(2500+5000)/2500
7500/2500
3
Moderator note:
It's not clear to me what you mean by "if you reduce this down to ... (expression in n)". It would help to define the general case that you are looking at.
Instead of using 100001 I simplified it to 101-199, which allowed me to determine the equation to be: n^2 + 100n/n^2... which is a much simpler mathematical equation. I 'm guessing, I could have simplified the equation w/o plugging in the numbers for a refined answer, but I found it easier to do the math in this example.
Sum of n odd terms = n 2
n =( last term +1) / 2
--> n=50000.
Now express all numbers in terms of 100000 and take it common.
100000+3,10000+5,.....,100000+99999 = 1 + 3 + 5 + 7 + . . . + 9 9 9 9 9 ( 1 0 0 0 0 0 × n ) + 1 + 3 + 5 + 7 . . . . + 9 9 9 9 9 = ( n 2 ) ( 1 0 0 0 0 0 × n ) + ( n 2 ) = n 1 0 0 0 0 0 + 1 ; n=50000 = 2 + 1 = 3
1 + 3 + 5 + … + 9 9 9 9 9 1 0 0 0 0 1 + 1 0 0 0 0 3 + 1 0 0 0 0 5 + … + 1 9 9 9 9 9 = 1 + 3 + 5 + … + 9 9 9 9 9 1 0 0 0 0 0 + … + 1 0 0 0 0 0 + 1 + 3 + 5 + … + 9 9 9 9 9 = 1 + 3 + 5 + … + 9 9 9 9 9 5 0 0 0 0 ⋅ 1 0 0 0 0 0 + 1 + 3 + 5 + … + 9 9 9 9 9 = 5 0 0 0 0 2 5 0 0 0 0 ⋅ 1 0 0 0 0 0 + 1 = 2 + 1 = 3
Both Nr. & dr are Aps, No. of termsof Nr= (199999 -100001)/2 + 1=49999, no. of terms in Dr. also 49999, Then, Sum of Nr / Dr =n/2(a +an) divided by n/2(b+bn) = 49999/2(100001+199999) by49999/2x(1+99999) = 150000/50000 =3
Numerator can be totalled by adding 2 pairs --> 100001 + 199999, 100003 + 199997 and so on for 50000 times ==> 300000 * 50000 Denominator is similarly --> 1+99999, 3+99997 and so on for 50000 times ==> 100000 * 50000 Numerator / Denominator = 300000/100000 = 3!
Numerator:
First, pair up the first and last terms, then the second and second-to-last terms, and so on.
100,001 + 199,999 = 300,000, and 100,003 + 199,997 = 300,000, etc.
From 100,001 to 200,000 (counting the even numbers), there are 100,000 numbers, and therefore 50,000 pairs that add up to 300 ,000. Since we are dealing with the sum of the odd pairs only, there are 25 ,00 pairs that add up to 300,000. For simplicity, we will not evaluate this yet. Instead, the sum of the numerator is
300,000 x 25,000
Denominator:
Using the same idea:
1 + 99 999 = 100 000, 3 + 99 997 = 100 000, etc.
From 1 to 100,000, there are 100,000 numbers, or 50,000 pairs that add up to 100,000. There are 25,000 odd-number pairs. The sum is
100,000 x 25,000
Final Sum:
=(300,000 x 25,000) / (100,000 x 25,000)
=(300,000) / (100,000 ), where the 25,000s cancel out.
= 3
(100000+1+100000+3+...)/1+3+5.... A total of 50000 nos so (100000*50000 + 50000^2)/50000^2 = 3 (since 1+3+5+...n= n^2)
for denominator part summation of no.s is (99999 100000/2)-49999 50000=2500000000, for numerator we can write 100000+1+100000+2+100000+3+.........+100000+99999= 5000000000+2500000000=7500000000, 7500000000/2500000000=3
Finding the two sums and then dividing is the hard way. The average term on top is the average of 1 0 0 , 0 0 1 and 1 9 9 , 9 9 9 ; thus it is 1 5 0 , 0 0 0 . The average on the bottom is similarly found; it is 5 0 , 0 0 0 . And the top and the bottom have equally many terms. So it's just 1 5 0 , 0 0 0 / 5 0 , 0 0 0 , which is 3 .
I'd have written 1 + 3 + 5 + 7 + 9 + 1 1 + ⋯ + 9 9 9 9 9 (with \cdots) or at least 1 + 3 + 5 + 7 + 9 + 1 1 + … + 9 9 9 9 9 rather than 1 + 3 + 5 + 7 + 9 + 1 1 + . . . + 9 9 9 9 9 (with just three dots: ... ). Notice the resulting asymmetry: the leftmost dot is closer to the nearby plus sign than the rightmost dot is to its nearby plus sign. And if you do this is genuine LaTeX (which is not limited to math notation) as opposed to this stripped-down thing, the use of actual dots will neglect proper spacing between the dots.
The numerator can be (100000+100000+100000+... 50000times) + 1+3 +5+....+99999. This latter portion can be divided by denominator to give 1. Now, (100000+100000+...) can be written as 100000 X 50000. The denominator can, among other things be seen as an Arithmetic Progression with a=1, n=50000, d=2. Therefore, the sum of the denominator is 25 X (10^8) after calculations. Thus, (5 X (10^9))/(25 X (10^8))=2. The answer, 2+1=3
Notice that 1+3+5+...+2n-1=n^2. One can prove this using mathematical induction. Therefore if ...+99999=2n-1 then n=50000. Therefore
(100000n+n^2)/n^2=(100000+n)/n=150000/50000=15/5=3
let the no of terms of denominator be 'n' and its sum be 's'. we can write the numerator as 10000+1+10000+3+10000+5.......... so,the eqn would become (10000 n+ s)/s. we know that , for an AP, s= (n/2) (a1+aN). a1 + aN =10000. so s= (n/2)*10000. apply it in the eqn.....the answer is 3.
calculate n by using An=a+(n-1)d, we get n=50000,here the series is in AP.sum of n terms in AP S=n/2(a+l)........by substuting we get 3 isthe answer..............
let f be that fraction
numerator become (3/2)*9999900000=n (say)
and denominator becomes (1/2)*9999900000=d (say)
hence f becomes n/d = 3
hence the result.
Applying
odd nos. sum theorem n^2
and last no. 99999=2n-1,
we get sum as 50000^2,
now on numerator writing 100001/100003....as 100000+1/100000+3...., and then simplifying
we get 100000*50000+50000^2 as numerator
and denominator is 50000^2,
dividing and solving we get 3 as answer.
no of terms in numerator are 50000 and the sum of 1st and last term is 300000 similarly 2nd and 2nd last then we get( 25000)(300000) and denominator (25000)(100000) and answer is 3
let us divide the problem into two parts, a = (100000+100000+......+100000)/(1+3+5+......+99999) and b = (1+3+5+.....+99999)/(1+3+5+........+99999). It is obvious that b=1. now coming to a we see that every pair p and (n-p+1) adds up to 100000 making the total sum of the denominator half of that of the numerator. So a = 2 and hence the number = a+b, i.e. 2+1 = 3
The number of terms is series, n= (99,999+1)/2 = 50,000. odd series.
The numerator of this fraction can be re-written as( (100000+1) + (100000+3) + (100000+5) + ... (100000+99999) ) On rearranging, we get numerator as (100000+100000+... 50,000 times) (1+3+5+...99999) which is denominator itself.
so fraction simplies to (100,000)(50,000) (1+3+5+...99999) + 1
denominator can be rewritten as 50,000^2 , summation of odd series.
hence the fraction becomes (100,000)(50,000) /(50,000^2) + 1 which gives 2+1 = 3
The sum of the first n positive odd integers is n^2, so the denominator works out to (50,000)^2.
Rewrite the numerator as (100,000 + 1) + (100,000 + 3) + ....... + (100,000 + 99,999), which simplifies to (100,000)(50,000) + (50,000)^2
Now you can break up the fraction as [(100,000)(50,000)]/(50000)^2 + 1 = 2 + 1 = 3
Write a solution. Numerator and dr contains same number of terms ,so only ist term + last term /1st term + last term =300000/100000=3
= (100000 * n + x)/x where x = (1+3+5+...+99999) also x= 100000 n/2 so, (100000 * n + x)/x = (100000 * n +100000 n/2)/(100000 n/2) = 3

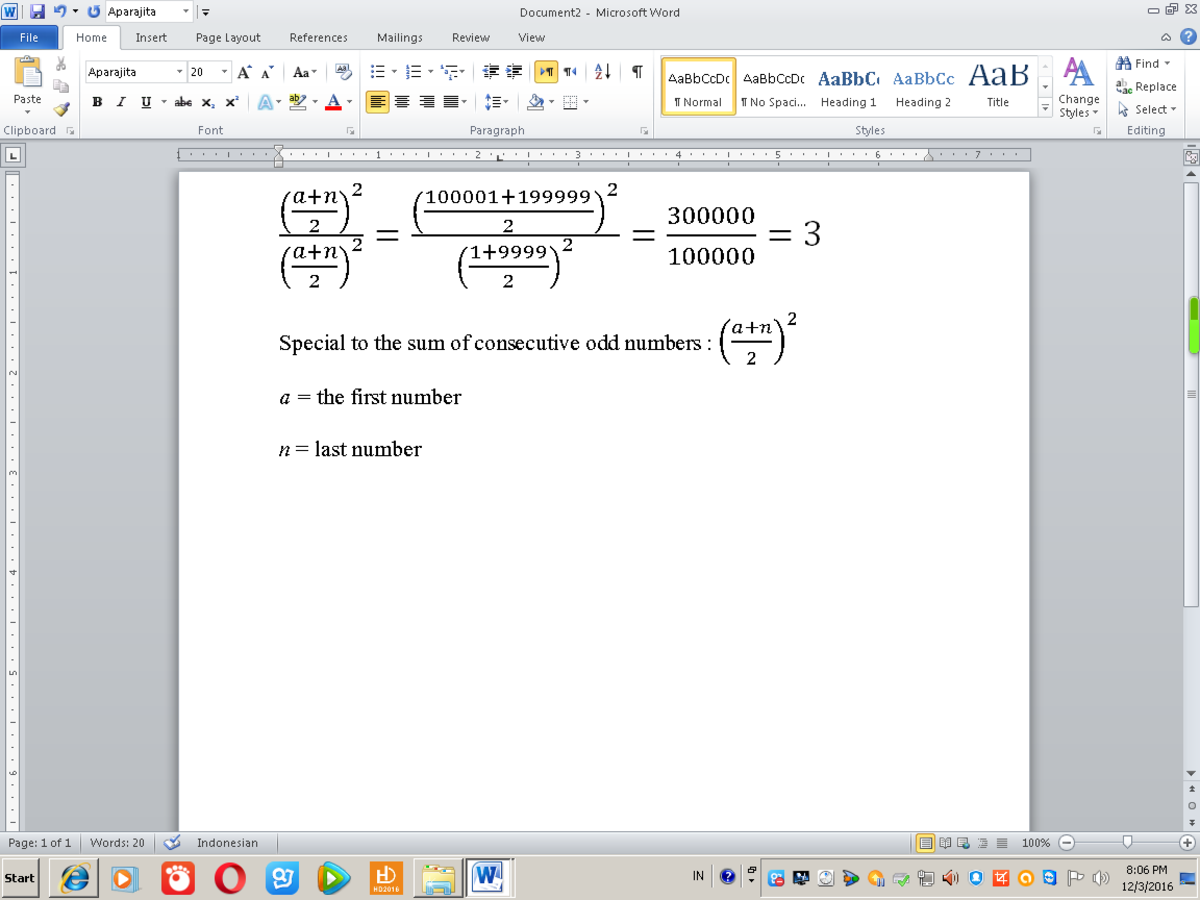
The sum S of an arithmetic progression of n terms is given by: S = 2 n ( a + l ) , where a and l are the first and last terms respectively.
Therefore,
1 + 3 + 5 + 7 + 9 + 1 1 . . . + 9 9 9 9 9 1 0 0 0 0 1 + 1 0 0 0 0 3 + 1 0 0 0 0 5 + . . . + 1 9 9 9 9 9
= 2 n ( a 2 + l 2 ) 2 n ( a 1 + l 1 ) = 2 5 0 0 0 0 ( 1 + 9 9 9 9 9 ) 2 5 0 0 0 0 ( 1 0 0 0 0 1 + 1 9 9 9 9 9 ) = 1 0 0 0 0 0 3 0 0 0 0 0 = 3