An Old Sangaku Problem
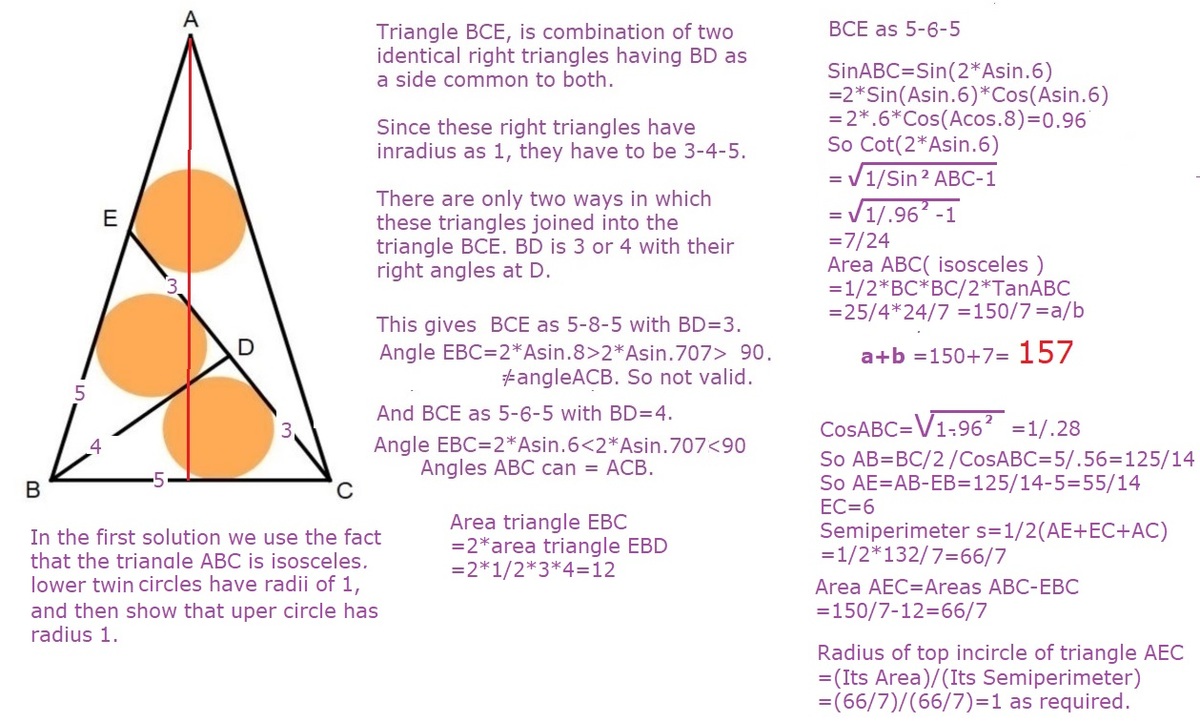
In an isosceles triangle △ A B C , two equal right triangles △ B C D and △ B D E are drawn. Three identical circles of radius 1 are inscribed inside the triangles as shown:

The area of the isosceles △ A B C can be expressed as b a , where a and b are coprime positive integers. Find the sum a + b .
The answer is 157.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Nice solution Sir!
For the sake of plurality, let’s see a solution that bypasses trigonometry, using exclusively Euclidean geometry tools.

First notice that Δ B C D = Δ B E D .
Let
F
,
G
,
H
,
K
,
L
,
Q
,
S
,
T
be points of tangency and
I
1
,
I
2
,
I
3
the centres of the three circles,
C
N
=
h
(
C
N
⊥
A
B
)
, a as seen in the picture.
Label
B
F
=
B
H
=
B
G
=
a
,
C
F
=
C
K
=
E
G
=
E
L
=
b
,
A
S
=
A
T
=
c
,
E
Q
=
E
S
=
x
(groups of equal tangent segments).
E I 1 and E I 2 are angle bisectors of ∠ A E C and ∠ B E C , thus θ + φ = 9 0 ∘ . Consequently, Δ E I 2 L and Δ E I 1 Q are similar right-angled triangles, hence
1 x = b 1 ⇒ x = b 1 ( 1 ) By Pythagorean theorem on Δ B C D , ( a + b ) 2 = ( a + 1 ) 2 + ( b + 1 ) 2 and this leads to a b = a + b + 1 ( 2 ) Moreover, A B = A C ⇒ B S = C T ⇒ B S = C Q ⇒ a + b + x = b + 1 + 1 + b − x ⇒ 2 x = b − a + 2 ( 3 ) Combining ( 1 ) , ( 2 ) and ( 3 ) , we get to the equation b 3 − 5 b + 2 = 0 which can be written as ( b − 2 ) ( b + 1 + 2 ) ( b + 1 − 2 ) = 0 Thus, b = 2 , or b = 2 − 1 ( b is positive). But the last solution leads to a negative value for a , therefor it is rejected.
Hence, b = 2 , so ( 2 ) gives a = 3 and ( 1 ) ⇒ x = 2 1 .
This means that triangles
Δ
B
C
D
and
Δ
B
E
D
are
3-4-5 right-angled triangles
.
(It is so gratifying how often we come across this triangle in Sangaku Problems!)
Now, we move to the calculations of areas.
By Heron’ s formula, for Δ B C E , which has B C = B E = 5 and C E = 6 , we get a r e a o f Δ B C E = 1 2 .
Alongside, we have a r e a o f Δ B C E = 2 1 B E ⋅ h ⇒ 1 2 = 2 1 × 5 × h ⇒ h = 5 2 4 .
For the area of Δ A E C we use both formulae: A = r s , where r is the inradius, s is the semierimeter and A = 2 1 A E ⋅ h .
s = 2 A E + E C + C A = 2 2 A S + 2 E S + 2 C Q = c + x + ( C E − x ) = c + 6 .
A r e a o f Δ A E C = 1 ⋅ ( c + 6 ) = c + 6
On the other hand, a r e a o f Δ A E C = 2 1 ( c + x ) ⋅ h = 2 1 ( c + 2 1 ) ⋅ 5 2 4 = 5 1 2 c + 5 6 .
Hence, 5 1 2 c + 5 6 = c + 6 ⇒ c = 7 2 4 .
Finally, a r e a o f Δ A B C = 2 1 A B ⋅ h = 2 1 ( a + b + c + x ) ⋅ h = 7 1 5 0 and 1 5 0 + 7 = 1 5 7
Impeccable approach Sir!
Log in to reply
Thanks a lot. I'm still trying to understand your solution though... Can you, please, elaborate on it a little more?
Log in to reply
Sir which portion of my solution? how I got BD = 4 , I reckon?
Log in to reply
@Nibedan Mukherjee – Yes, but to begin with: How does a "Lateral inversion of Square KDJM along its side JM" result to square FG'LJ'?
Log in to reply
@Thanos Petropoulos – Consider triangles BED & BDC. Both are congruent. Since BE= BC, taking the mirror image of triangle BDC and placing it on triangle BDE along it's hypotenuse BE, results to rectangle FEDB, with FB = ED & FE = BD
Nice solution! By the way, do you have a Euclidean solution to your problem A small red segment and an angle ? I was able to find a trigonometric one but not a Euclidean one.
Log in to reply
Thank you David! In fact I do have one. I'll post it in a few days, as soon as I find the time. It's not a very short one.
Hi David! I finally posted a Euclidean solution to A small red segment and an angle . I hope you like it.
The only way I know how to solve this. Planned to post, but online games got in the way.
Let ∠ E B D = ∠ D B C = θ and t = tan 2 θ . Then D B = t 1 + 1 = t 1 + t ; E D = D B × tan θ = × 1 + t 1 − t 2 2 t = 1 − t 2 ; and E C = 2 × E D = 1 − t 4 . But also E C = tan 2 ∠ A E D 1 + tan 2 ∠ A C D 1 . Then we have:
tan ( 4 5 ∘ + 2 θ ) 1 + tan ( 2 3 θ − 4 5 ∘ ) 1 1 + t 1 − t + 1 − 3 t 2 3 t − t 3 − 1 1 − 3 t 2 3 t − t 3 + 1 1 + t 1 − t − 1 − 3 t − 3 t 2 + t 3 1 + 3 t − 3 t 2 − t 3 1 + t 1 − t − ( 1 + t ) ( 1 − 4 t + t 2 ) ( 1 − t ) ( 1 + 4 t + t 2 ) ( 1 + t ) ( 1 − 4 t + t 2 ) 8 t ( t − 1 ) − 2 t + 4 t 2 − 2 t 3 3 t 3 − 7 t 2 − t + 1 ( 3 t − 1 ) ( t 2 − 2 t − 1 ) t ⟹ t = tan 2 θ = 1 − t 4 = 1 − t 4 = 1 − t 4 = 1 − t 4 = 1 − t 4 = 1 − 3 t − 3 t 2 + t 3 = 0 = 0 = 3 1 , 1 + 2 , 1 − 2 = 3 1 For acute θ
Then B D = t 1 + 1 = 4 and E D = D B = 1 − t 2 = 3 . Therefore, E B = B C = 5 . The area of △ A B C = 2 1 × B C × 2 B C × tan ( 2 θ ) = 4 2 5 × 1 − tan 2 θ 2 tan θ = 4 2 5 × 7 2 4 = 7 1 5 0 . Therefore a + b = 1 5 0 + 7 = 1 5 7 .
It seems to me that your are assuming that the line G G ′ through G parallel to E C is tangential to the two incircles. In other words, you are assuming that B D = 4 , rather than proving it...
The (3,4,5) triangle notoriously has inradius 1 .
Suppose that triangles D C B and D E B are both (3,4,5) triangles. It is a bit of easy trigonometry to deduce that B A = C A = 1 4 1 2 5 , and that A E = 1 4 5 5 . Thus triangle A E C has semiperimeter 7 6 6 .
On the other hand triangle A B C has area 7 1 5 0 , so that A E C has area 7 6 6 . Thus A E C also has inradius 1 , which means that these are the correct dimensions for this sangaku. Thus the desired answer is 1 5 0 + 7 = 1 5 7 .
For a more analytic solution, suppose that the smaller acute angle in D B C is α , so that ∠ D B C = ∠ D B E = α . Suppose also that B C = B E = R . Then triangle B D C has area 2 1 R 2 sin α cos α = 4 1 R 2 sin 2 α and semiperimeter 2 1 R ( 1 + sin α cos α , and hence both D B C and D B E have inradius r 0 = 2 ( 1 + sin α + cos α ) R sin 2 α On the other hand A B + A C = 2 1 R sec 2 α , so that A E = 2 1 R ( sec 2 α − 2 ) . Also A B C has area 4 1 R 2 tan 2 α , and hence A E C has area 4 1 R 2 ( tan 2 α − 2 sin 2 α ) . Moreover A E C has semiperimeter 2 1 R ( sec 2 α − 1 + 2 sin α ) , and hence A E C has inradius r 1 = 2 ( 1 − cos 2 α + 2 sin α cos 2 α ) R 2 sin 2 α ( 1 − 2 cos 2 α ) Since r 0 = r 1 we deduce that 1 − cos 2 α + 2 sin α cos 2 α ( 4 cos 2 α − 1 ) sin α = ( 1 − 2 cos 2 α ) ( 1 + sin α + cos α ) = ( 1 − 2 cos 2 α ) ( 1 + cos α ) + cos 2 α − 1 Thus ( 4 cos 2 α − 1 ) 2 cos 2 α + [ ( 1 − 2 cos 2 α ) ( 1 + cos α ) + cos 2 α − 1 ] 2 = ( 4 cos 2 α − 1 ) 2 which leads us to the sextic equation 8 0 cos 6 α + 1 6 cos 5 α − 1 6 4 cos 4 α − 1 2 cos 3 α + 1 1 4 cos 2 α − 2 4 2 ( 4 cos 2 α − 3 ) ( 2 cos 2 α − 1 ) ( 5 cos α − 4 ) ( cos α + 1 ) = 0 = 0 Since α is acute, we see that either cos α = 2 1 3 or cos α = 2 1 or cos α = 5 4 . However, in the first case we must have α = 3 0 ∘ and the above equation relating sin α and cos α would imply that sin α = − 2 1 , which is impossible. Similarly, in the second case we would have to have α = 4 5 ∘ , and the above equation would again tell us that sin α had to be negative. Thus the only possiblility is that cos α = 5 4 , and so the (3,4,5) solution is the only one.
Let's see how many others have a hunch as good as yours.
I'm going to remember that the inradius of the 3-4-5 is 1. Now as for the circumradius....
Log in to reply
The circumradius is 2 5 , since the hypotenuse is a diameter.
Log in to reply
Thats the joke
Log in to reply
@Razzi Masroor – Don’t give up the day job.
Log in to reply
@Mark Hennings – I actually knew that the perimeter was double the area( as a neat fact) though I honestly didn't consider that this makes the inradius 1.
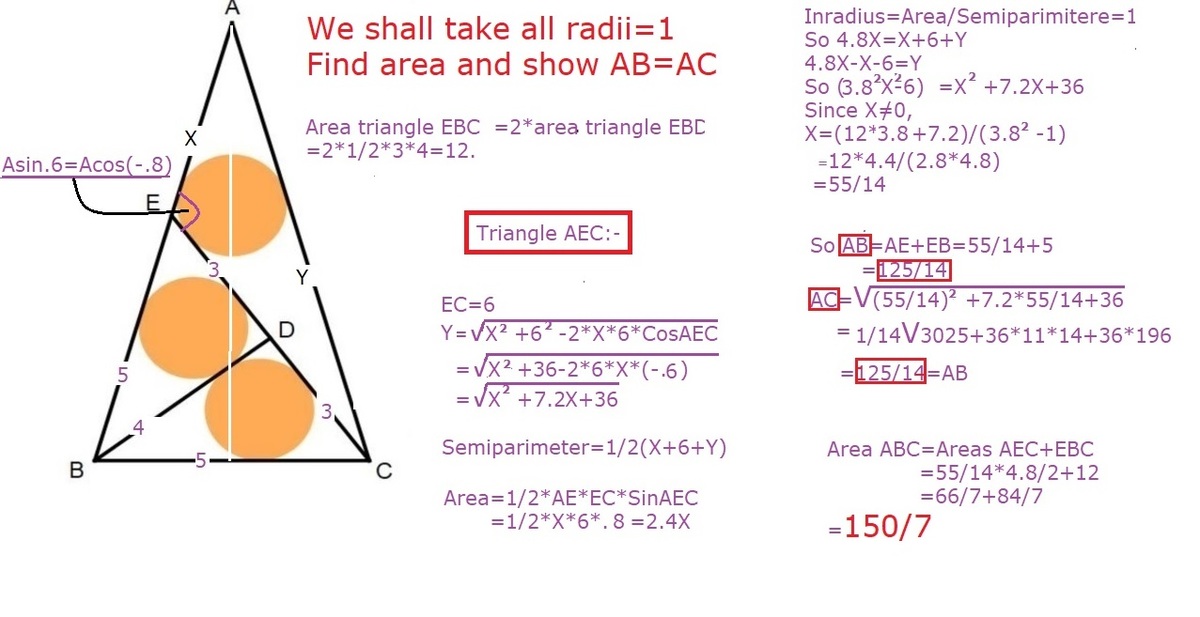
Write expressions of radius of inscribed circle for right triangle and general upper triangle in term of sides. Further, sum the areas of two right and one general triangle to large isosceles triangle. Solve the system of equations with WolframAlpha to get base of isosceles triangle as 5 and other two sides equal to 5+(55/14) each.
Area=(150/7)
Answer=157
Lots of good solutions here.
I found the best way for me to visualise the problem was to make the line EDC horizontal with the circles below ED and DC fixed. Let's call the circle below ED '1' and the circle below DC '2'.
Then imagine the third inscribed circle as a boulder being pushed along the EDC line. Because the other two circles are fixed the location of the third circle (or boulder) determines the length of AB and AC and ED and DC. With the midpoints of circle 1 and circle 2 fixed therefore the line connecting the midpoint of circle 1 to the midpoint of the boulder is parallel to the line AB. And with the information provided we can use trigonometry to work out the various angles and lengths and where the boulder needs to be located so that ABC is isosceles.
And knowledge that a 345 triangle has an inscribed circle of radius 1 is helpful (yet can lead to a miscalculation due to complacency :)) but not necessary for those without knowledge and the above is one way of looking at the problem.

Method 1:
Let F be the point of tangency between A and E , G be the point of tangency between E and B , H be the point of tangency between B and C , J be the point of tangency between A and C , I 1 be the center of the incircle in △ A E C , I 2 be the center of the incircle in △ B E D , and I 3 be the center of the incircle in △ B D C .
Also let θ = ∠ D B C = ∠ D B E . Then ∠ A B C = ∠ A C B = 2 θ and ∠ B E D = ∠ B C D = 9 0 ° − θ , which means ∠ A C E = 3 θ − 9 0 ° and ∠ C E A = 9 0 ° + θ .
By properties of an incircle, ∠ H B I 3 = 2 1 θ , since the incircle has a radius of 1 , H I 3 = 1 . Then by trigonometry on △ B H I 3 , B H = cot 2 1 θ . By a similar argument and letting t = cot 2 1 θ , B G = cot 2 1 θ = t , G E = cot ( 4 5 ° − 2 1 θ ) = t − 1 t + 1 , E F = cot ( 4 5 ° + 2 1 θ ) = t + 1 t − 1 , A F = A J = cot ( 9 0 ° − 2 θ ) = ( t 2 − 2 t − 1 ) ( t 2 + 2 t − 1 ) 4 t ( t 2 − 1 ) , and J C = cot ( 2 3 θ − 4 5 ° ) = t 3 − 3 t 2 − 3 t + 1 − t 3 − 3 t 2 + 3 t + 1 . Since △ A B C is an isosceles triangle, A B = A C , so that:
t + t − 1 t + 1 + t + 1 t − 1 = t 3 − 3 t 2 − 3 t + 1 − t 3 − 3 t 2 + 3 t + 1
which simplifies to:
( t − 3 ) ( t 2 + 1 ) ( t 2 + 2 t − 1 ) = 0
so that t = 3 or t = 2 − 1 for t > 0 , but only t = 3 leads to a positive solution for G E = t + 1 t − 1 .
Therefore t = 3 , so B C = t + t − 1 t + 1 = 3 + 3 − 1 3 + 1 = 5 and A C = A B = ( t 2 − 2 t − 1 ) ( t 2 + 2 t − 1 ) 4 t ( t 2 − 1 ) + t 3 − 3 t 2 − 3 t + 1 − t 3 − 3 t 2 + 3 t + 1 = ( 3 2 − 2 ⋅ 3 − 1 ) ( 3 2 + 2 ⋅ 3 − 1 ) 4 ⋅ 3 ( 3 2 − 1 ) + 3 3 − 3 ⋅ 3 2 − 3 ⋅ 3 + 1 − 3 3 − 3 ⋅ 3 2 + 3 ⋅ 3 + 1 = 1 4 1 2 5 , so that the area by Heron's Formula is A △ A B C = 7 1 5 0 , and 1 5 0 + 7 = 1 5 7 .
Method 2:
Let a = D C = D E , b = B D , c = B C = B E , d = A C = A B , and θ = ∠ D B C = ∠ D B E .
Since △ A B C is an isosceles triangle, ∠ A B C = ∠ A C B = 2 θ and ∠ B A C = 1 8 0 ° − 4 θ .
From △ B D C , sin θ = c a , cos θ = c b , and
a 2 + b 2 = c 2
From the double angle formulas, sin 2 θ = c 2 2 a b and cos 2 θ = c 2 b 2 − a 2 and sin 4 θ = c 4 4 a b ( b 2 − a 2 ) .
By the law of sines on △ A B C , c sin ( 1 8 0 ° − 4 θ ) = d sin 2 θ , which after substitution and rearranging simplifies to:
d = 2 ( b 2 − a 2 ) c 3
Since A = s r for the area A , semiperimeter s , and inradius r of a triangle, and the inradius of △ D B C and △ A E C is r = 1 , A = s . Then for △ D B C ,
2 1 a b = 2 1 ( a + b + c )
and for △ A E C , 2 1 d ( d − c ) sin 4 θ = 2 1 ( d − c + d + 2 a ) , which after substitution and rearranging simplifies to:
2 a b ( d − c ) = c ( 2 a + 2 d − c )
These four equations simplify to:
( a − 3 ) ( a 2 − 2 ) ( 3 a 2 − 6 a + 2 ) = 0
so that a = 3 , a = 2 , or a = 1 ± 3 3 for a > 0 , but only a = 3 leads to a positive solution for b = a − 2 2 ( a − 1 ) .
Therefore, a = 3 , b = 4 , c = 5 , and d = 1 4 1 2 5 , and the area of △ A B C is A △ A B C = 2 1 d 2 sin ( 1 8 0 ° − 4 θ ) = 2 1 d 2 ⋅ c 4 4 a b ( b 2 − a 2 ) = 7 1 5 0 , and 1 5 0 + 7 = 1 5 7 .