And that is Mechanics
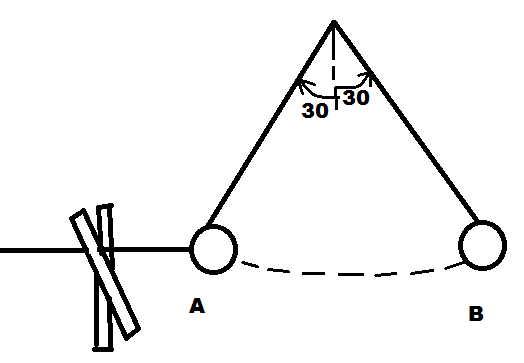
A ball is held at rest at position A by two light strings. The horizontal string is cut and the ball starts swinging as a pendulum. Point B is the farthest to the right the ball goes as it swings back and forth. What is the ratio of the tension in the supporting string at position B to its value at A before the horizontal string was cut?
The answer is 0.75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Why you are breaking MG component in 2nd equation to find t3 and why not break t3 component t3cos 30 and equate it with mg?
If you have done so then why in first equation you have broken tension into components? Please explain
Summing the forces at point B in the vertical direction yields T B cos 3 0 = m g ⟹ T B = 3 2 m g . Why can't this be true?
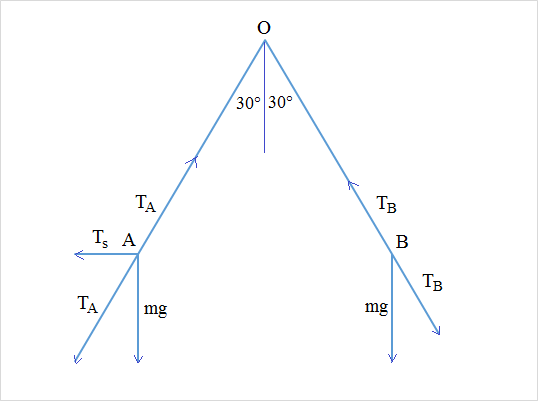
At position B, the ball is momentary stop. There is no centripetal force and the forces involve are the weight of the ball ( m g ) and the tension in the pendulum string ( T B ). By the Newton's third law of motion, we have T B = m g cos 3 0 ∘ = 2 3 m g .
At position A, there are three forces acting: the weight of the ball ( W = m g ), the tension in the pendulum string ( T A ) and the tension in the horizontal string ( T s ). By the Newton's third law of motion, we have T A = W + T s (vector addition) ⟹ T A = cos 3 0 ∘ m g = 3 2 m g .
Therefore, T A T B = 3 2 m g 2 3 m g = 4 3 = 0 . 7 5 .
Summing the forces at point B in the vertical direction yields T B cos 3 0 = m g ⟹ T B = 3 2 m g . Why can't this be true?
Log in to reply
T B is a reactive force (Newton's third law). If m g is not there, there is no tension. It T B cos 3 0 ∘ = m g , then there will be a horizontal force T B sin 3 0 ∘ which has no balancing force.
Log in to reply
@Chew-Seong Cheong Do you mean to say that we can take components of T A because there is a balancing force both horizontally and vertically?
To find the tension in the string at position A, identify all forces acting on the object. There is a tension force T 1 acting at 60 degree angle to the horizontal. A second tension force T 2 acts directly to the left of the object, and weight m g acts directly downward. Because the object is in static equilibrium, the sum of all forces in the x and y directions must equal zero. Therefore, summing forces in y direction results in:
T 1 s i n ( 6 0 ) − m g = 0
Solving for T 1 ,
T 1 = s i n ( 6 0 ) m g = 3 2 m g
Now for Point B, two forces act on the object: a tension force T 3 again at 60 degree angle and weight m g downward. Because Point B is the farthest the pendulum can go, the object is at maximum gravitational potential and has no kinetic energy. Therefore, radial acceleration, which depends on velocity, is zero as well. Summing forces along the direction of the radial acceleration vector (pointing toward the center of the pendulum) gives:
T 3 − m g c o s ( 3 0 ) = 0
Solving for T 3 ,
T 3 = m g c o s ( 3 0 ) N = 2 ( 3 ) m g
T 1 T 3 = 3 2 m g 2 ( 3 ) m g = ( 2 ( 3 ) m g ) ( 2 m g ( 3 ) ) = 0 . 7 5