Angel angle

Geometry Level 1

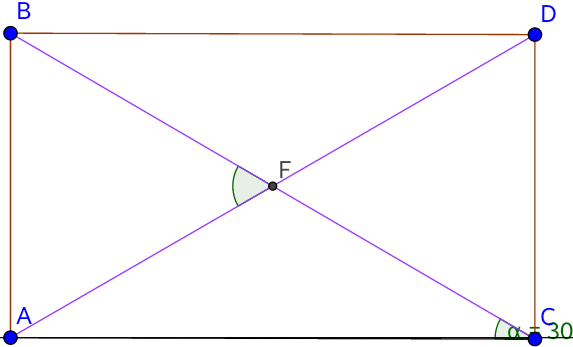
In the above figure, $ABDC$ is a rectangle where $\angle{BCA} = {30}^\circ$ . Find the measure of $\angle{BFA}$ in degrees.

The answer is 60.

2 solutions

Ashish Menon
Apr 26, 2016

Relevant wiki: Congruent and Similar Triangles

Let $AC$ be $x$ . Let $AB = CD = y$ .
Then, by Pythagoras' theorem,
$BC = AD = \sqrt{x^2 + y^2}$
Now, for $\triangle{BCA}$ and $\triangle{DAC}$ ,
$AD = CD$ (opposite sides of rectangle)
$AC = CA$ (common side)
$BC = AD$ (proved above)
$\therefore$ $\triangle{BCA}$ is congruent to $\triangle{DAC}$
So, $\angle {BCA} = \angle {DAC} = {30}°$ (corresponding parts of congruebt triangles)
$\therefore$ $\angle{BFA} = {30}° + {30}° = \boxed{{60}°}$ (ext. angle = sum of interior opp. angles)

Angle AFB is the exterior angle, So 30+30 = 60.

Why overcomplicate?

Mehul Arora - 5 years, 1 month ago

Overcomplicate?

Ashish Menon - 5 years, 1 month ago

This is too much calculation for a simple problem, don't you think?

Mehul Arora - 5 years, 1 month ago

@Mehul Arora – Hm.... ok. I will look next time

Ashish Menon - 5 years, 1 month ago

@Ashish Menon – That's okay, it's your perception. Just saying, try to minimize your effort by taking the shortest way out ;)

Mehul Arora - 5 years, 1 month ago

@Mehul Arora – Ok, initially i thought of saying that FC = FA = FB, So, a circle qould pass through A, B and C, so the angle at the circumference would be twuce that at the centre. Buy I was not sure if it was correct.

Ashish Menon - 5 years, 1 month ago

Syed Hamza Khalid
Dec 27, 2018

$\triangle ABF$ is equilateral so $\angle BFA = 60°$

Hint: Note that $\triangle ACD$ and $\triangle BCD$ are $30-60-90$ triangle

Angel angle

The answer is 60.

2 solutions

0 pending reports