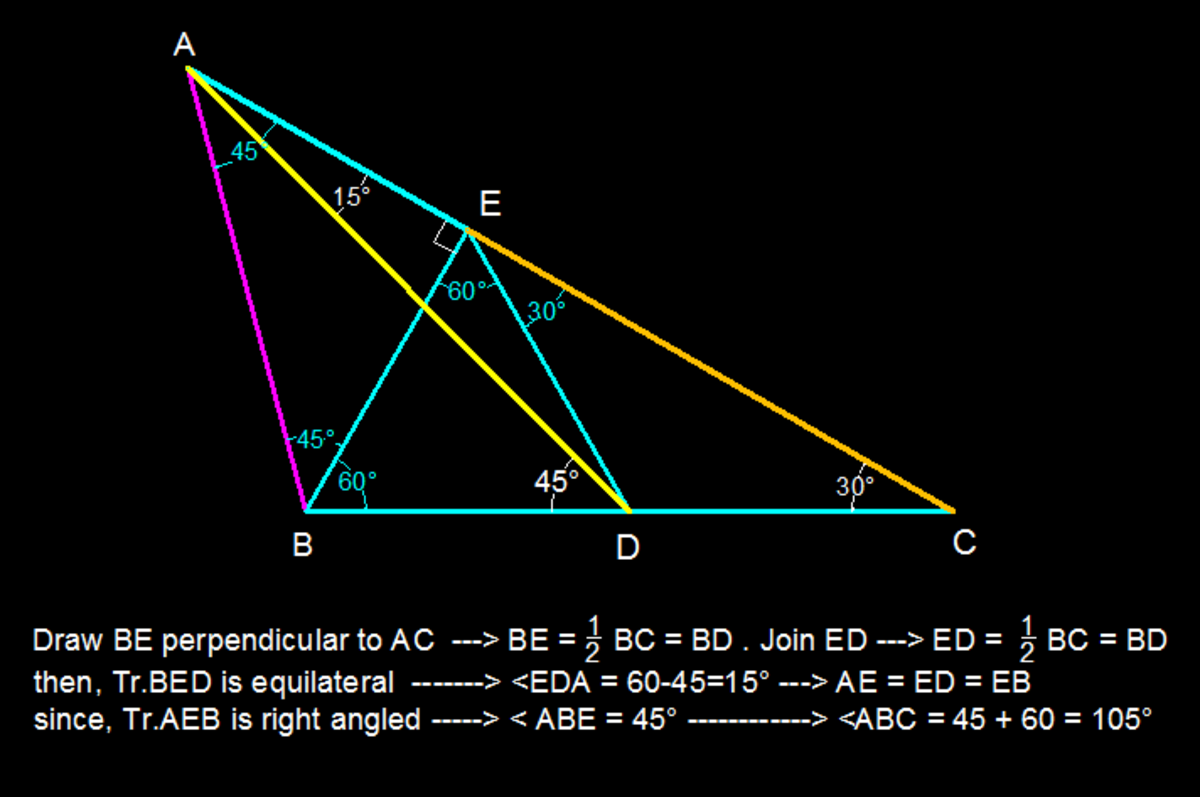
Angle ABC
In a triangle A B C , D is the midpoint of B C . Join A D . Angle A D B = 4 5 degree and angle A C B = 3 0 degree. Find angle A B C
The answer is 105.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let ∣ C D ∣ = ∣ D B ∣ = x . Next, drop a perpendicular from A to the line extending through C B , letting the point of intersection be P . Now let ∣ A P ∣ = y and ∣ B P ∣ = z .
Then tan ( ∠ A C B ) = tan ( 3 0 ∘ ) = 2 x + z y ⟹ 2 x + z = 3 y and
tan ( ∠ A D B ) = tan ( 4 5 ∘ ) = x + z y ⟹ x + z = y .
So 2 ( x + z ) − ( 2 x + z ) = 2 y − 3 y ⟹ z = ( 2 − 3 ) y ⟹ z y = 2 − 3 1 = 2 + 3 .
But z y = tan ( ∠ A B P ) ⟹ ∠ A B P = tan − 1 ( 2 + 3 ) = 7 5 ∘ .
(Proof: tan ( 7 5 ∘ ) = tan ( 3 0 ∘ + 4 5 ∘ ) = 1 − tan ( 3 0 ∘ ) tan ( 4 5 ∘ ) tan ( 3 0 ∘ + tan ( 4 5 ∘ ) =
1 − 3 1 3 1 + 1 = 3 − 1 3 + 1 = 2 ( 3 + 1 ) 2 = 2 + 3 . )
Finally, we see that ∠ A B C = 1 8 0 ∘ − ∠ A B P = 1 8 0 ∘ − 7 5 ∘ = 1 0 5 ∘ .
I tried this problem twice, and both times came up with the
7
5
.
I created point P on
A
C
such that
D
P
is perpendicular to
A
C
.
I also designated DP to equal 10 units (I often do this on geometry problems looking for angles).
Then I simply chased the angles by trig ratios, law of cosines and law of sines. Here's what I got:
D
C
=
2
0
B
D
=
2
0
P
C
=
1
7
.
3
2
A
P
=
3
7
.
3
2
A
D
=
3
8
.
6
4
A
B
=
2
8
.
2
9
∠
A
B
C
=
7
5
Log in to reply
I like that approach. I get the same values except for the last, and I suspect that the fact that sin ( 7 5 ) = sin ( 1 0 5 ) may be the reason for the difference. Note that ∣ A C ∣ = ∣ A P ∣ + ∣ P C ∣ = 5 4 . 6 4 . Then ∣ A C ∣ cos ( 3 0 ) = 4 7 . 3 2 , which exceeds ∣ B C ∣ = ∣ D C ∣ + ∣ B D ∣ = 4 0 . This implies that ∠ A B C must be obtuse, as the perpendicular dropped from A will intersect the line extended from side B C at a point outside the triangle.
Log in to reply
After posting I walked away from it, and then yes, I did recall my unit circle and sin75 = sin 105. I'm guessing though that we sketched up the problem differently Brian. My sketch met all of the criteria, as did yours I assume. My method does not require <ABC to be obtuse. Recheck it. My math is solid. There just exists two answers to this question as posited. You can sketch it up with <ABC being acute and meeting the same initial criteria. Try it.
Log in to reply
@Ken Hodson – I'm sorry we're at odds here, but I just can't see how ∠ A B C can be acute. I did try again using some graph paper. I drew the base B C and placed D at the midpoint. I then drew a line at 3 0 ∘ above B C passing through C and a line 4 5 ∘ above B C passing through D , (both lines ascending from right to left), making their point of intersection the vertex A . Drawn this way, the projection of A to the horizontal lies beyond B , implying that ∠ A B C is obtuse. How does your sketch differ from this construction? I'm keeping an open mind, but I just can't see at the moment how else to construct the specified triangle.
From Tr. ADC, AC/AD= Sin(135°)/sin(30°) =√2 or AC²=2 AD². Further, by Apollonius, AB² + AC² = 2BD²+ 2AD². In other words, AB²=2BD²=BD BC. This implies, by the power point theorem, that AB is tangent to the circum-circle of Tr. ADC. Hence / BAD= / ACD = 30° (Alternate Segment Theorem) which implies that /_ABC=75°
Without loss of generality, let BC=2. S o B D = D C = 1 . ∠ C A D = 1 5 . ∠ A D C = 1 3 5 , ∠ D A B = 1 3 5 − B . Applying Sin Law to Δ A D B a n d Δ A D C , w e h a v e : − S i n D A B B D ∗ S i n B = A D = S i n C A D D C ∗ S i n 3 0 . S u b s t i t u t i n g t h e v a l u e s , S i n ( 1 3 5 − B ) 1 ∗ S i n ( B ) = S i n 1 5 1 ∗ S i n 3 0 = 2 ∗ C o s 1 5 . S i n ( B ) S i n ( 1 3 5 − B ) = 2 1 ∗ ( C o t B + 1 ) = 2 ∗ C o s 1 5 1 ⟹ C o t B = 2 ∗ C o s 1 5 1 − 1 . ∴ B = − 7 5 O R 1 0 5 o . B = 1 0 5 o