Angle Bisector?

Let $NX$ be the bisector of $\angle MNP$ and $MX=28$ , $XP=12$ .

Given: $MN-NP=18$ .... $(1)$

By angle bisector theorem.

$\dfrac{MN}{MX}=\dfrac{NP}{XP}$

$\dfrac{MN}{28}=\dfrac{NP}{12}$

$\dfrac{MN}{NP}=\dfrac{7}{3}$

Adding $(-1)$ to both sides.

$\dfrac{MN-NP}{NP}=\dfrac{4}{3}$

$\dfrac{18}{NP}=\dfrac{4}{3}$

$NP=\dfrac{27}{2}$

From $(1)$ .

$MN=\dfrac{63}{2}$

Now, the perimeter of $\triangle MNP$ .

$NP+MN+(MX+XP)$

$\dfrac{27}{2}+\dfrac{63}{2}+40=\boxed{85}$

Let $MN$ be $x$ , $NP$ be $y$ and the point where the angle bisector and the side $MP$ meet be $A.$ Also let $MA=28$ and $AP=12.$
So, according to the question $x-y=18\Rightarrow x=y+18.$ According to the angle bisector theorem: $\frac{MN}{MA}=\frac{NP}{PA}$
Now, $\frac{x}{28}=\frac{y}{12}$
$\Rightarrow$ $\frac{y+18}{28}=\frac{y}{12}$ (substitute $x=y+18$ )
$\Rightarrow 28y=(y+18)(12)$
$\Rightarrow$ $28y=12y+216$
$\Rightarrow$ $16y=216$
$y=13.5.$
$x=y+18\Rightarrow x=13.5+18\rightarrow x=31.5$
So,the perimeter of the triangle $=NP+MN+MA+AP=13.5+31.5+28+12=\boxed{85}.$

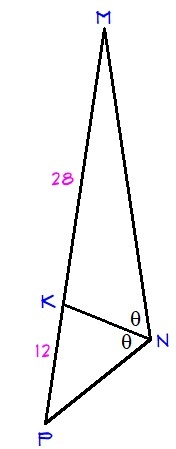
By the angle bisector theorem , we have

$\dfrac{MK}{KP}=\dfrac{MN}{PN}$

$\dfrac{28}{12}=\dfrac{MN}{NP}$

$28NP=12(18+NP)$

$28NP=216+12NP$

$16NP=216$

$NP=13.5$

It follows that $MN=31.5$ .

Thus,

$P=28+12+13.5+31.5=$ $\boxed{85}$

Note:

From $MN-NP=18$ , we get $MN=18+NP$