Angle bisector problem
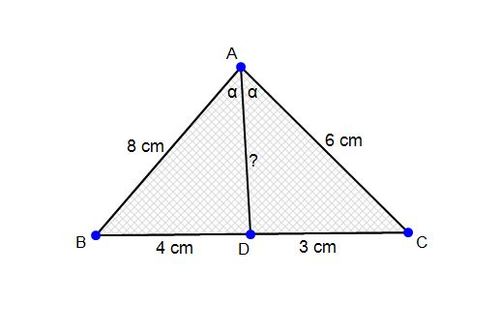 In the figure above,
A
D
is the bisector of
∠
A
, with lengths
A
B
=
8
,
A
C
=
6
,
B
D
=
4
and
D
C
=
3
. Find the length of
A
D
.
In the figure above,
A
D
is the bisector of
∠
A
, with lengths
A
B
=
8
,
A
C
=
6
,
B
D
=
4
and
D
C
=
3
. Find the length of
A
D
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Now that came from stewart's theorem
Log in to reply
Thanks for telling. I did not know the name of the theorem.
Log in to reply
Actually Stewat's theorem is BC(AD^2+BD.CD)=AB^2.CD+AC^2.BD,Now if AD is the angle bisector then,AB/AC=BD/CD,so replce it in Stewart's theorem,you will get AB.AC=AD^2+BD.CD,I think you need to edit your because it will be AC instead of BC
Log in to reply
@Rifath Rahman – ok. I have edited it. Thank you for telling.
Can you please prove the theorem,you stated in your solution.
Thanks!
I have solved this question by applying Cosine formula.
Log in to reply
@Akhil Bansal One proof of this theorem is by cosine rule only. If you want that please tell me
Log in to reply
Please,i would love to see it..
Log in to reply
@Akhil Bansal – https://en.wikipedia.org/wiki/Stewart%27s_theorem you can take a look at it here.
We can do this by direct formula ,
t B C = A B + A C 2 A B ⋅ A C ⋅ s ( s − B C )
Here ,
t B C → Angle bisector on B C .
s → Semi-perimeter.
After calculation, Answer = 6
For the formula, go here: https://proofwiki.org/wiki/Length of Angle_Bisector
that page is empty!!!
Stewarts theorem gives AD^2=(8 8 3+6 6 4)/(4+3)-4*3=36. AD=6.
There is a theorem that AB × AC = A D 2 + BD × DC
If you want a proof then comment below and I will add one.
Now, applying the theorem, we get
8 × 6 = A D 2 + 4 × 3
48 = A D 2 + 12
A D 2 = 36
AD = 6cm
Hence the answer is 6cm