Angle Chasing, huh?
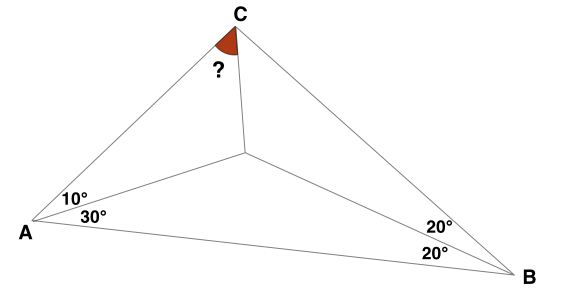
In the above figure, find the measure of the red angle in degrees.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Moderator note:
Great solution adding in that point, forming a ton of isosceles triangles.
This is really cool !
Very nice!
Good solution
Moderator note:
Nice solution with setting up the trigonometric forms.
You could have used trigonometric version of Ceva theorem to solve it in a more fast and short way.
Can you please explain the last equation and how you went from s i n x = 2 s i n 1 0 s i n ( 1 0 0 − x ) to s i n x = c o s ( 9 0 − x ) − c o s ( 1 1 0 − x )
Log in to reply
Use the identity 2 s i n A s i n B = c o s ( A − B ) − c o s ( A + B ) .
hey i get an equation in terms of θ can u please solve it for me ??
Log in to reply
What is it ?
Log in to reply
@Venkata Karthik Bandaru – it goes like this= s i n ( 6 0 + θ ) s i n 2 0 = s i n ( 1 7 0 − θ ) s i n 1 0 Solve for θ
Log in to reply
@Chirayu Bhardwaj – Hey, your equation is right. I just plugged in θ = 2 0 ∘ and found that the equation is true. Here is the way to solve the equation :
s i n ( 6 0 + θ ) s i n 2 0 = s i n ( 1 7 0 − θ ) s i n 1 0 ⇒ 2 s i n ( 2 0 ∘ ) s i n ( 1 7 0 ∘ − θ ) = 2 s i n ( 1 0 ∘ ) s i n ( 6 0 ∘ + θ ) . Now apply the identity 2 s i n A s i n B = c o s ( A − B ) − c o s ( A + B ) and simplify. Hope this helps.
@Venkata Karthik Bandaru – Are u solving ??
Good solution.
SOLVED THE SAME WAY .........DUDE!!!!!!!
Plenty of efforts are required to visualize but way of trigonometry is simplest and best for convincing.
I did in geometry which found coordinates of M and C and tan θ = ∣ 1 + m 1 m 2 m 1 − m 2 ∣ for θ = 2 0 ∘ . This way can hardly make mistake and fast to visualize but the mathematics went through ought to be slightly more complicated. B is assigned as (1, 0).


I used the sine rule a couple of times to determine that the right-most of the inner triangles was isosceles. Given that the outer triangle was also isosceles it was plain sailing with the sum of angles in a triangle
Did the same brother!
Great solution
I will use the law of sines on three triangles to get to the solution.
Identity I: C M s i n ( 2 0 ° ) = B M s i n ( 1 0 0 ° − θ ) on triangle BCM, which can be written as:
B M = C M ∗ s i n ( 2 0 ° ) s i n ( 1 0 0 ° − θ )
Identity II: C M s i n ( 1 0 ° ) = A M s i n ( θ ) on triangle ACM, which can be written as:
A M 1 = s i n ( 1 0 ° ) ∗ C M s i n ( θ )
Identity III: B M s i n ( 3 0 ° ) = A M s i n ( 2 0 ° ) on triangle ABM, which can be written as:
A M B M = s i n ( 2 0 ° ) s i n ( 3 0 ° )
Now, if we multiply the first two identities, we get: A M B M = s i n ( 2 0 ° ) ∗ s i n ( θ ) s i n ( 1 0 ° ) ∗ s i n ( 1 0 0 ° − θ )
From here, we derive that: s i n ( 2 0 ° ) s i n ( 3 0 ° ) = s i n ( 2 0 ° ) ∗ s i n ( θ ) s i n ( 1 0 ° ) ∗ s i n ( 1 0 0 ° − θ ) , which can be simplified to: s i n ( 3 0 ° ) ∗ s i n ( θ ) = s i n ( 1 0 ° ) ∗ s i n ( 1 0 0 ° − θ ) .
Now, s i n ( 1 0 0 ° − θ ) = s i n ( 9 0 ° + 1 0 ° − θ ) , which also can be written as c o s ( 1 0 ° − θ ) . Plugging it back into the previous equality:
s i n ( 3 0 ° ) ∗ s i n ( θ ) = s i n ( 1 0 ° ) ∗ c o s ( 1 0 ° − θ ) .
The left hand side can be broken into the sum of two sines divided by two:
s i n ( 1 0 ° ) ∗ c o s ( 1 0 ° − θ ) = 2 1 ∗ ( s i n ( 2 0 ° − θ ) + s i n ( θ ) )
And since we also know that s i n ( 3 0 ° ) = 2 1 , we can rewrite the equality again yielding:
2 s i n ( θ ) = 2 s i n ( 2 0 ° − θ ) + s i n ( θ )
Therefore, 2 s i n ( 2 0 ° − θ ) = 0 → s i n ( 2 0 ° − θ ) = 0
This would potentially yield an infinitude of solutions, yet since we know that theta is an interior angle of a triangle (therefore 0 < θ < 1 8 0 ) as well as it is an angle no greater than 1 0 0 ° , we see that the only possible solution is θ = 2 0 ° .
In the above question let the required angle be θ , then using Trigonometric form of Ceva's theorem, we have
( s i n θ )( s i n 3 0 ∘ )( s i n 2 0 ∘ )=( s i n 1 0 0 ∘ − θ )( s i n 1 0 ∘ )( s i n 2 0 ∘ )
This amounts to ( s i n θ )=2( s i n 1 0 0 ∘ − θ )( s i n 1 0 ∘ )
which upon simplifying using 2( s i n A )( s i n B )=( c o s A − B ) - ( c o s A + B ) gives
c o s ( 1 1 0 ∘ − θ )=0
⟹ θ = 2 0 ∘
And yes, it is equivalent to using the sine rule many times.
The whole triangle has angles 40, 40, 100 so is isosceles. Let the two equal sides be x
Use the cosine rule to get the third side to be x multiplied by root(2-2cos100) = 1.532x
Use the sine rule to get the length from the point inside the main triangle to the right corner to be 1.532x times sin(30)/ sin(130) = x
Now this makes the internal triangle on the right isosceles with apex angle 20, so base angles both 80
Since the main triangle has an angle of 100 at the top, the red part must be 100-80 = 20
Call the centre O,so OA/OB=sin(20°)/sin(30°) sine theorem for triangle ABO,
Also from sine theorem for triangles AOC and BCO we have
put x=<OCA,then <BCO=180°-(20°+20°+30°+10°+x)=100°-x
so AO/OC=sin(x)/sin(10°) , OB/OC=sin(100°-x)/sin(20°)
so AO/OB=(sin(x)/sin(10°))/(sin(100°-x)/sin(20°))=sin(20°)/(0.5)
so 0.5 sin(x)sin(20°)=sin(10°)sin(20°) sin(100°-x)
so 0.5sin(x)=sin(10°)*sin(100°-x)
sin(x)=2sin(10°) (cos(10°) cos(x)+sin(10°)sin(x))
sin(x) cos(20°)=sin(20°) cos(x)
tg(x)=tg(20°)
so x=20° or x=200° but because x<100°
we choose x=20°
angle {bca}={cab}=40° so side cb=CA=p. put side AB=u ,,cos(40)=p^2+u^2-p^2÷(2pu.cos40) so u=2cos40.p. I used a graphical solution by assuming side p & draw the triangle 3 times with 3 different values of side p and every time by using angular scaler the unknown angle equal to 20 degree .
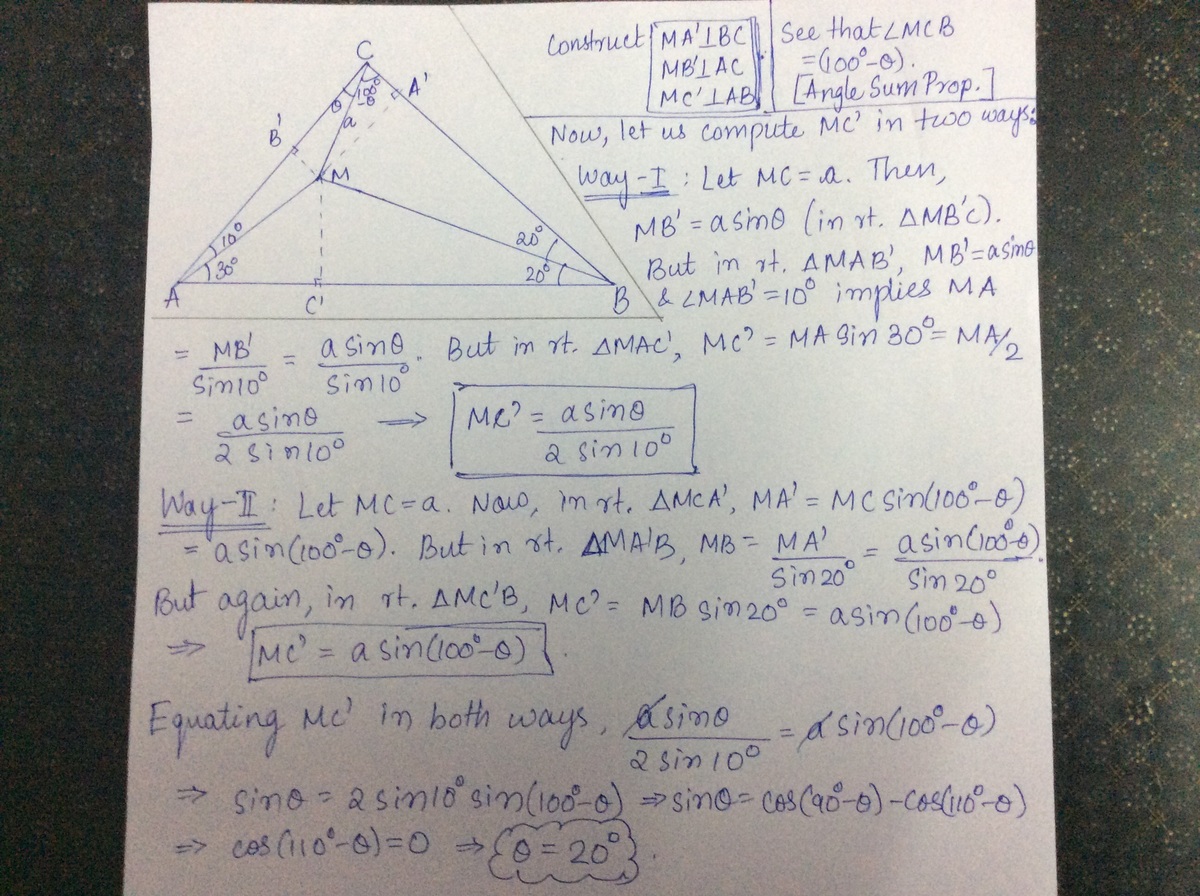
Yes, you can totally angle chase this problem. First, recognize that the large triangle is an isosceles triangle, and then draw in the lines as shown in graphic. The rest is easy angle chasing, especially after identifying a couple more isosceles triangles.