Angle-finding problem
Given that A and B are distinct point on a circle with centre O and diameter M N . If ∠ O A P = ∠ O B P = 1 0 ° and ∠ A O M = 4 0 ° . Find the measure of ∠ B O N in degrees.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
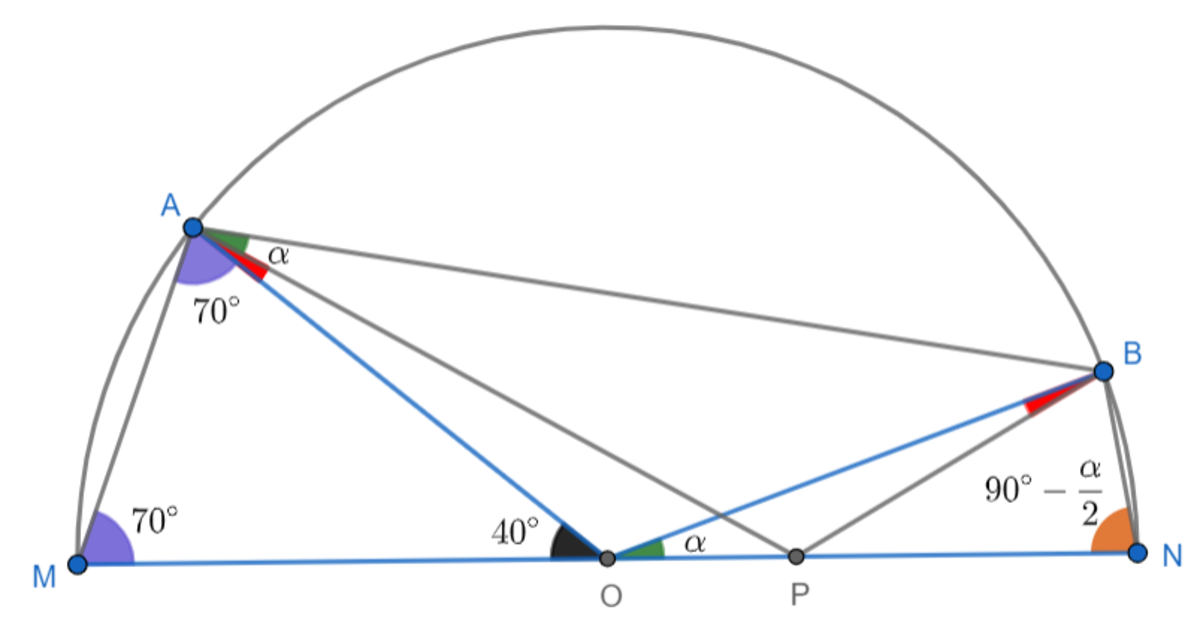 Since
∠
O
A
P
=
∠
O
B
P
=
1
0
∘
, quadrilateral
A
B
P
O
is
cyclic
. So, we have,
∠
B
O
P
=
∠
B
A
P
=
α
Also,
O
M
=
O
A
=
O
B
=
O
N
=
r
, where
r
is the radius of the semicircle. So,
△
A
O
M
and
△
B
O
N
are isosceles. Simple angle chasing leads to
∠
M
A
O
∠
B
N
O
=
2
1
8
0
∘
−
4
0
∘
=
7
0
∘
=
2
1
8
0
∘
−
α
=
9
0
∘
−
2
α
Since quadrilateral
M
A
B
N
is cyclic,
∠
M
A
B
∠
M
A
O
+
∠
O
A
P
+
∠
B
A
P
7
0
∘
+
1
0
∘
+
α
⟹
α
=
1
8
0
∘
−
∠
B
N
M
=
1
8
0
∘
−
∠
B
N
O
=
1
8
0
∘
−
(
9
0
∘
−
2
α
)
=
2
0
∘
Therefore, the required angle is
∠
B
O
P
=
2
0
∘
Since
∠
O
A
P
=
∠
O
B
P
=
1
0
∘
, quadrilateral
A
B
P
O
is
cyclic
. So, we have,
∠
B
O
P
=
∠
B
A
P
=
α
Also,
O
M
=
O
A
=
O
B
=
O
N
=
r
, where
r
is the radius of the semicircle. So,
△
A
O
M
and
△
B
O
N
are isosceles. Simple angle chasing leads to
∠
M
A
O
∠
B
N
O
=
2
1
8
0
∘
−
4
0
∘
=
7
0
∘
=
2
1
8
0
∘
−
α
=
9
0
∘
−
2
α
Since quadrilateral
M
A
B
N
is cyclic,
∠
M
A
B
∠
M
A
O
+
∠
O
A
P
+
∠
B
A
P
7
0
∘
+
1
0
∘
+
α
⟹
α
=
1
8
0
∘
−
∠
B
N
M
=
1
8
0
∘
−
∠
B
N
O
=
1
8
0
∘
−
(
9
0
∘
−
2
α
)
=
2
0
∘
Therefore, the required angle is
∠
B
O
P
=
2
0
∘
Rotate △ B O P counterclockwise about O so that B ′ coincides with A :
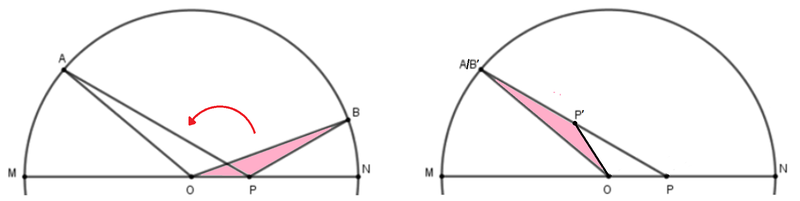
Then by the exterior angle theorem on △ A O P , ∠ A P O = ∠ A O M − ∠ O A P = 4 0 ° − 1 0 ° = 3 0 ° .
Since O P = O P ′ , △ O P P ′ is an isosceles triangle, so ∠ O P ′ P = ∠ O P P = 3 0 ° .
And by the exterior angle theorem on △ B ′ O P ′ , ∠ B ′ O P ′ = ∠ O P ′ P − ∠ O B ′ P ′ = 3 0 ° − 1 0 ° = 2 0 ° .
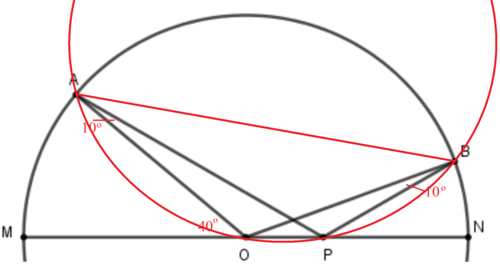
Since ∠ O A P = ∠ O B P , A B P O is a cyclic quadrilateral . Then ∠ A B P + ∠ A O P = 1 8 0 ∘ . This means that ∠ A B P = ∠ A O M = 4 0 ∘ . Since ∠ A B O = ∠ A B P − ∠ O B P = 4 0 ∘ − 1 0 ∘ = 3 0 ∘ . Note that △ A B O is isosceles, implying that ∠ O A B = ∠ A B O = 3 0 ∘ and ∠ A O B = 1 2 0 ∘ . Now ∠ B O N = 1 8 0 ∘ − ∠ A O B − ∠ A O M = 1 8 0 ∘ − 1 2 0 ∘ − 4 0 ∘ = 2 0 ∘ .
A cyclic quadrilateral is a quadrilateral that can be inscribed in a circle, meaning that there exists a circle that passes through all four vertices of the quadrilateral. But the vertices, P and O do not lie on the circle, then how is A B P O cyclic?
Log in to reply
Not the circle shown, but we can draw another circle that pass through the four vertices. I have added the circle. Refer to the link ( cyclic quadrilateral ) I have provided please
Log in to reply
Thanks, Sir for your courtesy. I really learned a new method to view things.