Angle hunting
The △ A B P , △ B C Q and △ A Q R satisfy the following:
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ ∠ B A P = ∠ C A R = 1 5 ∘ ∠ A B P = ∠ C P Q = 3 0 ∘ ∠ A C R = ∠ B C Q = 4 5 ∘
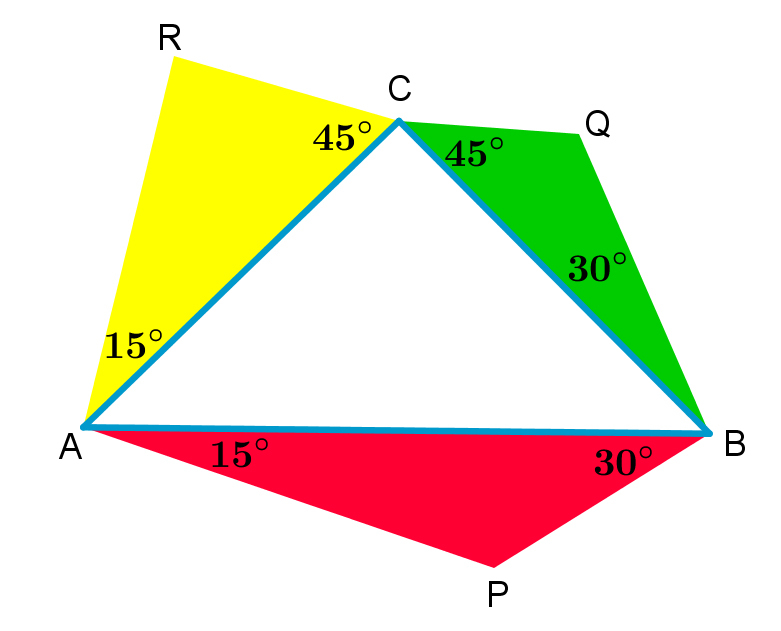
Find the largest angle of △ P Q R in degrees.
The answer is 75.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Is there a purely pure geometric way to solve this problem.
Log in to reply
There might be, but I couldn't find one.
Actually, I found the fact, that those points R,Q,P are the centres of inscribed circles if we build up a 90-60-30 triangles properly on sides of triangle ABC. Therefore, maybe Napoleon theorem could be used for inspiration to prove some facts related to problem.
Log in to reply
in this case AQ, BR and CP are concurrent. this can be proved by using very little trigonometry. but this fact is of no use. we need some creative constructions.
Log in to reply
@Srikanth Tupurani – another option is to draw angle bisectors of angles A,B and C. they intersect at H. from H draw perpendiculars to AR and AP. let them intersect at X,Y. also draw perpendiculars from H to BP and BQ. let them intersect at W and T. we get two cyclic quadrilaterals. Now we can draw the circumcirlces of the two cyclic quadrilaterals. we have two intersecting circles. and a point C outside. we can can convert this problem in to a totally different problem about circles. this may not lead to anything. i am not sure this will lead to solution.
Log in to reply
@Srikanth Tupurani – here another observation is perpendicular distance from H to AR=perpendicular distance from H to AP. similarly perpendicular distance from H to BP=perpendicular distance from H to BQ.
ok i got it. but still we need to work hard.
Since the angle sum of a triangle is 1 8 0 ° , ∠ A P B = 1 3 5 ° , ∠ A R C = 1 2 0 ° , and ∠ B Q C = 1 0 5 ° .
By the law of sines on △ A P B , △ A R C , and △ B Q C , A P = sin 1 3 5 ° sin 3 0 ° A B = 2 2 A B , B P = sin 1 3 5 ° sin 1 5 ° A B = 2 3 − 1 A B , A R = sin 1 2 0 ° sin 4 5 ° A C = 3 6 A C , C R = sin 1 2 0 ° sin 1 5 ° A C = 6 3 2 − 6 A C , B Q = sin 1 0 5 ° sin 4 5 ° B C = 2 3 − 1 B C , and C Q = sin 1 0 5 ° sin 3 0 ° B C = 2 6 − 2 B C .
By the law of cosines on △ A P R , △ B P Q , and △ C R Q ,
P R 2 = A P 2 + A R 2 − 2 ⋅ A P ⋅ A R ⋅ cos ( ∠ B A C + 3 0 ° )
P Q 2 = B P 2 + B Q 2 − 2 ⋅ B P ⋅ B Q ⋅ cos ( ∠ A B C + 6 0 ° )
Q R 2 = C Q 2 + C R 2 − 2 ⋅ C Q ⋅ C R ⋅ cos ( ∠ A C B + 9 0 ° )
Substituting the above values of A R , A P , B P , B Q , C Q , and C R , using the the identity cos ( a + b ) = cos a cos b − sin a sin b , the law of cosine formulas from △ A B C ( cos ∠ B A C = 2 ⋅ A C ⋅ A B A C 2 + A B 2 − B C 2 , cos ∠ A B C = 2 ⋅ A B ⋅ B C A B 2 + B C 2 − A C 2 , and cos ∠ A C B = 2 ⋅ A C ⋅ B C A C 2 + B C 2 − A B 2 ), and the area K formula from △ A B C ( K = 2 1 A C ⋅ B C sin ∠ A C B = 2 1 A B ⋅ A C sin ∠ B A C = 2 1 A B ⋅ B C sin ∠ A B C ), P R 2 , P Q 2 , and Q R 2 simplify to:
P R 2 = 2 1 B C 2 + 6 1 A C 2 + 3 2 3 K
P Q 2 = ( 3 − 2 3 3 ) B C 2 + ( 1 − 2 3 ) A C 2 + ( 4 3 − 6 ) K
Q R 2 = ( 2 − 3 ) B C 2 + ( 3 2 − 3 3 ) A C 2 + ( 3 8 3 − 4 ) K
Then by the law of cosines on △ P Q R , cos ∠ P R Q = 2 ⋅ P R ⋅ Q R P R 2 + Q R 2 − P Q 2 which simplifies to cos ∠ P R Q = 2 ( 2 1 + 2 3 ) B C 2 + ( − 6 1 − 3 3 + 2 3 ) A C 2 + ( 2 − 3 2 3 ) K 2 ( 2 1 + 2 3 ) B C 2 + ( − 6 1 − 3 3 + 2 3 ) A C 2 + ( 2 − 3 2 3 ) K , which reduces further to cos ∠ P R Q = 2 1 , meaning ∠ P R Q = 6 0 ° (regardless of △ A B C !)
Similarly, cos ∠ Q P R = 2 ⋅ P R ⋅ P Q P R 2 + P Q 2 − Q R 2 which simplifies to cos ∠ Q P R = 2 ( 4 3 2 + 4 6 ) B C 2 + ( 4 2 − 1 2 6 ) A C 2 + ( 6 − 2 ) K 2 2 ( ( 4 3 2 + 4 6 ) B C 2 + ( 4 2 − 1 2 6 ) A C 2 + ( 6 − 2 ) K ) , which reduces further to cos ∠ P R Q = 2 2 , meaning ∠ P R Q = 4 5 ° (also regardless of △ A B C ).
Finally, since the angle sum of a triangle is 1 8 0 ° , and since ∠ P R Q = 4 5 ° and ∠ P R Q = 6 0 ° , ∠ P R Q = 1 8 0 ° − 4 5 ° − 6 0 ° = 7 5 ° .
So regardless of △ A B C , the three angles in △ P Q R are always ∠ P R Q = 4 5 ° , ∠ P R Q = 6 0 ° , and ∠ P R Q = 7 5 ° , and the largest of these angles is 7 5 .