Angle In A Grid
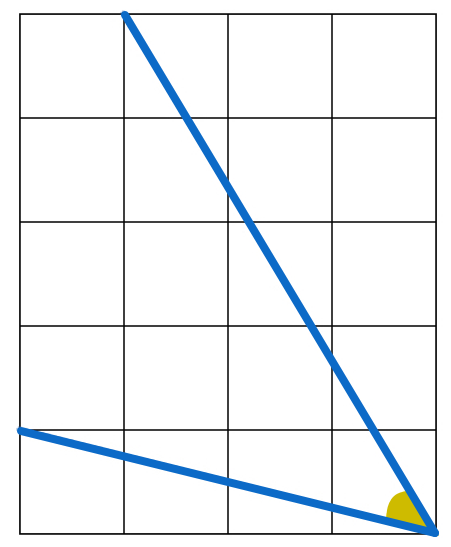
In the above square grid, what is the measure of the yellow angle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
"Do you see why?" Clearly the vectors ( − 4 , 1 ) and ( 1 , 4 ) are identical up to a rotation of a right angle. An excellent solution, Chung!
Log in to reply
That works too. Added rotation method into the solution :)
Except I mistyped the second vector; it should be ( 1 , 4 ) . For some reason Brilliant won't let me edit my comment.
Log in to reply
We are aware of the bug and are fixing it. I've edited the comment for you.
Please explain how you obtained the numbers in the first line of your solution.
Log in to reply
Just the slopes. Slope of AB = 5/3, and the angle w/ respect to horizontal must be arctan(slope). Same logic applies to BC. So the angle between AB and BC is the difference between the two
Log in to reply
If they are the slopes then shouldn't the slope of AB and BC be negative since as you move to the right the graph decreases?
From the picture we obtain the following triangle.

Let length of each square be x . Then in the bottom most triangle with hypotenuse CB,
C B 2 = ( 4 x ) 2 + ( x 2 ) = 1 7 x 2 C B = 1 7 x
Similarly,
A C = ( 4 x ) 2 + x 2 = 1 7 x A C = ( 5 x ) 2 + ( 3 x ) 2 = 3 4 x = 1 7 . 2 x
Therefore we get that ABC is an isosceles triangle. Now construct a perpendicular bisector D of AB from C.
Now, In triangle CDB,
∠ C D B = 9 0 D B = 2 1 7 . 2 x C B = 1 7 x
Therefore,
cos ( ∠ C D B ) = C B D B = 1 7 x 2 1 7 . 2 x = 2 1 cos ( ∠ C D B ) = cos ( 4 5 ) ∠ C D B = 4 5
Connecting AC is a good idea.
The proof can be greatly simplified without using trigo. Just notice that ∠ A C B = 9 0 ∘ , by considering the gradiants, or using pythagorean theorem
Log in to reply
Oh yeah, I didn't notice it while solving
Or avent easier: use the outside triangles. The angle being asked is: 90-arctan (1/4)-arctan (3/5).(Just count the squares to find 1/4 and 3/5.
Log in to reply
That works, but my idea is to avoid trigonometry completely. This problem can be answered with just basic geometry skills of recognizing the isosceles right triangle (of which I removed one leg).
Log in to reply
@Chung Kevin – True. I like your way to be honest!
Log in to reply
@Peter van der Linden – I'm trying to find more of such problems, but I can only find "trivial" instances of this setup. Any suggestions for to use "90 - arctan x - arctan y" to find such setups? I tried a few small values, but nothing seems to work out really well.
Log in to reply
@Chung Kevin – As it turns out, you will not be able to find other such angles, in the sense that the answer is either going to be 0, 45, 90, 135 for such a setup.
Another way of rephrasing your question (with Peter's tangent insight) is as follows:
If a , b are rational numbers, what rational multiple of π can be expressed in the form of tan − 1 a + tan − 1 b .
Now, using the following facts,
1.
tan
(
tan
−
1
a
+
tan
−
1
b
)
=
1
−
a
b
a
+
b
is also a rational number
2. The only rational values such that
tan
R
π
that are rational are
0
,
±
4
1
,
(
±
2
1
)
,
±
4
3
hence the "nice angles" are going to be 0, 45, 90, 135.
Really? And this is a level 2 question? I might as well get out my protractor. I thought there was going to be a really simple and intuitive way to find out this angle, but nope, it had to be complicated.
Log in to reply
You are only given the sides, so you can use trig functions. But you can also do it an elementary way, like in other comment. It's an isosceles right triangle. So, the angle is 45.
Really Nice Solution!! There is a little typo.. A C = s q r t 1 7 x and A B = s q r t 1 7 . s q r t 2 x
Yeah, well, I just saw it.
We have two vectors, with coordinates ( 4 , 1 ) and ( 3 , 5 ) . (I choose the negative x -axis to the left.)
Now I pick an orthogonal (angle-preserving!) linear transformation that makes the first vector parallel to the x -axis: ( x , y ) ↦ ( 4 x + y , x − 4 y ) . (In general, an orthogonal transformation is of the form ( x , y ) ↦ ( a x + b y , b x − a y ) .)
Apply this to the second vector: ( 3 , 5 ) ↦ ( 1 7 , − 1 7 ) , which clearly makes a 4 5 ∘ degree angle with the x -axis, and therefore with the first vector.
Note : In fact, we can save a lot of work by observing that a method like this will always result in rational values for the rotated vector ( x ′ , y ′ ) , which makes the tangent of the angle a rational number. This immediately excludes the angles 1 5 ∘ , 3 0 ∘ , and 6 0 ∘ , whose tangents are irrational algebraic numbers. With multiple-choice questions I love this kind of "cheating".
Connect the two lines to form an isosceles triangle. Now extend the grid to the right adding one column. Draw two more lines symmetrical to the shorter legs of that triangle to form a quadrilateral. Since all sides are equal, it is a rhombus. Draw the other diagonal. It is congruent to the existing diagonal (count the squares). So the rhombus is a square. The triangle is a right angle triangle, so the other (congruent) angles are (180 - 90) / 2 = 45
The yellow angle = 90 - t a n − 1 ( 4 1 ) − t a n − 1 ( 5 3 ) = 90 - 14 - 31 = 45
Connect up the other 2 points.
We now have an isosceles right triangle.
(Do you see why? You can either use the Pythagorean Theorem, calculate the gradient, or find a suitable rotation.)
Hence, the yellow angle is 4 5 ∘ .