Angle Tangled
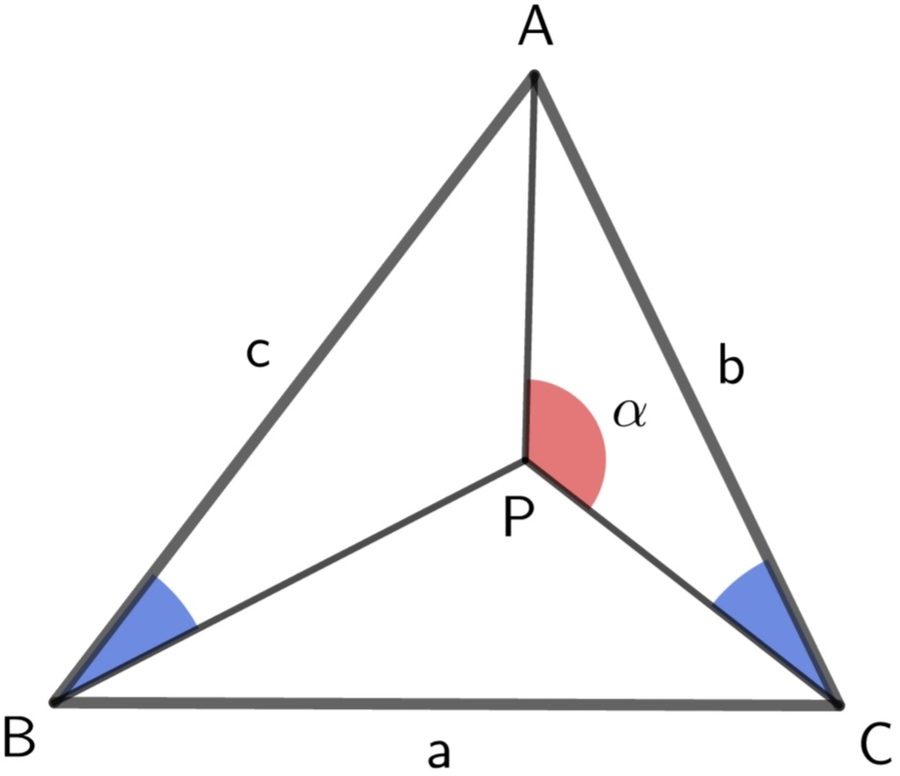 There is a point
P
inside
a triangle
△
A
B
C
such that
∠
P
B
A
=
∠
P
C
A
.
There is a point
P
inside
a triangle
△
A
B
C
such that
∠
P
B
A
=
∠
P
C
A
.
Let ∠ A P C = α . Find the conditions on the sides a , b , c of the triangle such that a minimum of α exists.
Let α min be the minimum value of α (if exists).
Submit your answer as the value of sin ( α min )
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let ∠ P B A = ∠ P C A = θ , ∠ B P C = x = ∠ A + 2 θ , ∠ A P B = β = 2 π − x − α .
Applying the sine rule for Δ A P B , Δ A P C , we get c sin β c sin α c sin α c sin α tan α ⟹ α ∴ d x d α = A P sin θ = b sin α = b sin ( 2 π − x − α ) = − b sin ( x + α ) = − b sin x cos α − b cos x sin α = c + b cos x − b sin x = tan − 1 ( c + b cos x − b sin x ) = ( c + b cos x ) 2 + ( b sin x ) 2 − b 2 − b c cos x
For an extremum, d x d α ( c + b cos x ) 2 + ( b sin x ) 2 − b 2 − b c cos x − b 2 − b c cos x ⟹ cos x = 0 = 0 = 0 = − c b
So, tan α ∴ sin α = c + b cos x − b sin x = c + b ( − c b ) − b ( c c 2 − b 2 ) = − c 2 − b 2 b = c b
As we can see from the expression for tan α , there is a radical c 2 − b 2 . So, for an extremum to exist, we need c > b . Also, we need the point P to stay inside Δ A B C . For that we need to satisfy 0 < θ < ∠ B . We can also write this in terms of x to get ∠ A < x < ∠ A + 2 ∠ B . This inequality can be written in terms of side lengths as c 2 − b 2 < a 2 < c 2 + 3 b 2 .
You might like to look at my solution to see where the conditions on a , b , c come from.
Log in to reply
I was able to get a 2 < c 2 + 3 b 2 from 0 < θ . For c 2 − b 2 < a 2 , I had to prove ∠ C < 2 π using θ < ∠ B ⟹ ∠ C < ∠ B + cos − 1 c b . I drew a circle of length c around A to prove it.
I am going through your solution, although I am not familiar with many of the terms that you used.
Let ∠ P B A = ∠ P C A = θ . Then ∠ B P C = 1 8 0 ∘ − ( B − θ ) − ( C − θ ) = 1 8 0 ∘ − B − C = 2 θ = A + 2 θ and ∠ A P B = 3 6 0 ∘ − A − 2 θ − α . Let A P = d . By sine rule ,
b sin α ⟹ b sin α c sin α = d sin θ = c sin ( 3 6 0 ∘ − A − 2 θ − α ) = c − sin ( A + 2 θ + α ) = − b sin ( A + 2 θ + α )
To find the minimum α , we first find the θ such that d θ d α = 0 .
c cos α d θ d α ⟹ d θ d α = − b cos ( A + 2 θ + α ) ( 2 + d θ d α ) = c cos α + b cos ( A + 2 θ + α ) − 2 b cos ( A + 2 θ + α )
We note that d θ d α = 0 , when A + 2 θ + α = 2 7 0 ∘ , since the angle is larger than 9 0 ∘ . Since
c sin α ⟹ sin α min = − b sin ( A + 2 θ + α ) = c − b sin 2 7 0 ∘ = c b
The minimum doesn't always exist. Can you figure out the conditions on the sides such that the minimum exists?
Log in to reply
In any configuration of a , b , c , there will be a range of values for α . And as long as there is a range of values, there will be a maximum and a minimum.
Log in to reply
Not necessarily. For example, what is the minimum value in the range ( 0 , 1 ) ? It doesn't exist.
Log in to reply
@Digvijay Singh – Well, you can then ask for infimum or supremum.
Log in to reply
@Atomsky Jahid – Yes, but I asked for a minimum here, which surely exists only when c > b and c 2 − b 2 < a < c 2 + 3 b 2
Log in to reply
@Digvijay Singh – Am I getting the definitions wrong? The maximum attainable value for sin α is c b . Are you implying sin α has a constant value when those conditions are met?
Log in to reply
@Atomsky Jahid – yes, when these conditions are met, then there is unique point P such that α attains a minimum value which is π − sin − 1 ( c b ) .
Log in to reply
@Digvijay Singh – Thanks. It looks like I confused α with sin α . I will have another look at the problem.
The conditions for a minimum to exist are:
-
c > b
-
c 2 − b 2 < a < c 2 + 3 b 2
Note that as Point P moves toward Point B, angle alpha decreases. Also, side b is opposite angle alpha. For the previous considerations, side c eventually approximates the hypotenuse of the minimum angle alpha. Q.E.D.:, by definition, the sine of angle alpha is opposite over hypotenuse, or b / c.
BTW, I'm not sure I could have deduced an answer if b / a was a distractor ...
Thus, if φ is minimized at some point internal to the triangle, then the minimum value of sin φ is c b . There are three conditions that the triangle has to satisfy for this minimum to be achieved in the desired manner, and they can most easily be expressed in terms of the angles of the triangle:
Using the Cosine Rule, and the known formula for the length of a triangle median, the conditions that B < C , C < 9 0 ∘ and ∠ C A M < 9 0 ∘ can be written in terms of the sides of the triangle as b < c , c 2 < a 2 + b 2 and a 2 < 3 b 2 + c 2 , respectively.