Angle trisection: A Beautiful problem
 Note: I give two explanations for this problem (both are the same thing) to make the problem more understandable.
Note: I give two explanations for this problem (both are the same thing) to make the problem more understandable.
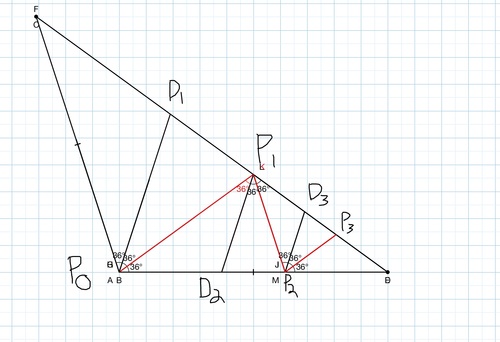
Let triangle △ A B P 0 be an obtuse isosceles triangle with ∠ B = 3 6 ∘ , ∠ P 0 = 1 0 8 ∘ , and segment A B = 2 0 1 5 .
Here is a general description of the pattern.
Angle ∠ B P 0 A is trisected by segments P 0 P 1 and P 0 D 1 where P 1 and D 1 are on side A B and B P 1 < B D 1
Next, angle P 0 P 1 B is trisected by segments P 1 P 2 and P 1 D 2 where P 1 and D 1 are on side P 0 B and P 2 B < D 2 B .
Here is an explicit description
Now, given the pattern above, let the point P n and D n be the points resulting from the trisection of ∠ P n − 2 P n − 1 B with B P n < B D n .
If P 6 P 7 P 9 P 1 0 can be expressed as ( c − a + b ) k where b is square free and a , c are co-prime positive integers and k is an integer, what is the value of a b c k ?
This is part of the set Trevor's Ten
Details and Assumptions
-
cos 3 6 = 4 1 + 5 . (And I know what you're thinking, the answer is not 20. Lol, if only it were that simple)
-
Hint: make an equation for P n − 1 P n . Don't work with numbers.
By the way, this problem is VERY beautiful and is without a doubt my new favorite problem that I've made.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Sorry @Trevor Arashiro , I didn't really like this problem because my extensive (and useless) math trivia knowledge made it trivial.
Log in to reply
Lol, I had to derive it.
Log in to reply
AMC 10B #22 also happened to be easy because of this useless trivia, so I guess it isn't that useless after all :3
Get ready for the mother of all solutions.
Well, to be exact, ϕ − 1
Incase you're wondering why this is my new favorite problem.
Now for the solution
Important Note: when we trisect the angle, two of the three smaller triangles are similar to the larger one. And when the angle of the smaller triangle is trisected, the two of the three smaller smaller triangles are similar, this continues for every trisection.
Let the "double leg" (is there a term for the leg that's used twice in an isosceles triangle) be x, the angle trisector segment be a, and the angle be 36. I'm not using a variable for cos ( 3 6 ) because for this problem, the angle 36 is unique. But for just one trisection, any angle can be used. This is because for any angle besides 36, when trisected, the triangles aren't similar.
By law of sines, we equate the area of the three smaller triangles to the area of the larger one. Using 2 1 a b sin ( c ) .
2 1 x 2 sin ( 3 ⋅ 3 6 ) = 2 1 x a sin ( 3 6 ) + 2 1 x a sin ( 3 6 ) + 2 1 a 2 sin ( 3 6 )
x 2 sin ( 3 ⋅ 3 6 ) = 2 x a sin ( 3 6 ) + a 2 sin ( 3 6 )
Let's derive the triple angle formula, shall we?
cos ( t ) + i sin ( t ) ^3 looking at the imaginary part.
sin ( 3 t ) = 3 cos 2 ( t ) sin ( t ) − sin 3 ( t )
sin ( 3 t ) = 3 sin ( t ) ( 1 − sin 2 ( t ) ) − sin 3 ( t )
sin ( 3 t ) = 3 sin ( t ) − 3 sin 3 ( t ) − sin 3 ( t )
sin ( 3 t ) = 3 sin ( t ) − 4 sin 3 ( t )
Using this identity
x 2 ( 3 sin ( 3 6 ) − 4 sin 3 ( 3 6 ) ) = 2 x a sin ( 3 6 ) + a 2 sin ( 3 6 )
Making this into a quadratic with a as the variable
0 = ( sin ( 3 6 ) ) a 2 + ( 2 x sin ( 3 6 ) ) a − x 2 ( 3 sin ( 3 6 ) − 4 sin 3 ( 3 6 ) )
Ugly as this may look, it's quite beautiful. Using the quadratic equation.
a = 2 sin ( 3 6 ) − 2 x sin ( 3 6 ) ± 4 x 2 sin 2 ( 3 6 ) − 4 ( sin ( 3 6 ) ( − 3 x 2 sin ( 3 6 ) + 4 x 2 sin ( 3 6 ) )
a = 2 sin ( 3 6 ) − 2 x sin ( 3 6 ) ± 4 x 2 sin 2 ( 3 6 ) + 1 2 x 2 sin 2 ( 3 6 ) − 1 6 x 2 sin 2 ( 3 6 )
a = 2 sin ( 3 6 ) − 2 x sin ( 3 6 ) ± 1 6 x 2 sin 2 ( 3 6 ) ( 1 − sin 2 ( 3 6 )
Using the identity cos 2 ( s ) = 1 − sin 2 ( s )
a = 2 sin ( 3 6 ) − 2 x sin ( 3 6 ) ± 4 x cos ( 3 6 ) sin ( 3 6 )
a = − x ± x cos ( 3 6 )
Since the side length can't be negative, we disregard the - case.
a = ( 2 cos ( 3 6 ) − 1 ) x
If you replace the 36 with θ , then this is the explicit formula for the length of an angle trisector of an isosceles triangle with side length x.
Now, since there is no constant term here
this is a ratio, aka: a scale factor since the triangles are similar
This means the ratio of P 0 B : P 0 P 1 = 1 : ( 2 cos ( 3 6 ) − 1 )
It follows that P 0 P 1 : P 1 P 2 = 1 : ( 2 cos ( 3 6 ) − 1 )
And that
P n − 1 P n : P n P n + 1 = 1 : ( 2 cos ( 3 6 ) − 1 )
And finally
P n − 1 P n : P n + k − 1 P n + k = 1 : ( 2 cos ( 3 6 ) − 1 ) k
Thus it follows that
P 6 P 7 P 9 P 1 0 = ( 2 cos ( 3 6 ) − 1 ) 3
Since k = 3
Plugging in our values (note that x=2015 is irrelevant to the problem, the information is extraneous) cos ( 3 6 ) = 4 1 ( 1 + 5 ) we get
( 2 − 1 + 5 ) 3
Thus ( z − x + y ) k , x=1, y=5, z=2, k=3
∴ x y z k = ( 1 ) ( 5 ) ( 2 ) ( 3 ) = 3 0
Well I liked this problem, (even if I did solve it the same way Daniel did). :) That is quite the solution you wrote, though. I started out misreading the question and thought we were trisecting the area and not the angle. Then there was no symmetry to exploit and it become quite the slog, at which point I re-read the question and then the sky opened and there were bunnies and rainbows all 'round. :D
You "finished" the set 41 minutes ahead of me. Sigh.... At least I finished before Jon Haussmann, so I can at least feel good about that.
Log in to reply
Hahah glad to hear you liked it. Btw, I couldn't stop laughing at the "bunnies and rainbows part" XD. And lol, you're still first, I didn't finish the set technially since I knew all the answers.
I think you could have used similar triangles instead of that heavy trisector calculation to prove that the ratio between side lengths is 2 cos ( 3 6 ∘ ) − 1 . Good work on writing that solution though.
Log in to reply
I basically used similar triangles, but I show a derivation for a triangle of any angle. If you replace 36 with θ
@Brian Charlesworth congrats on being the first person to finish all 11 problems!
Log in to reply
Haha. I just posted my comment and then saw your congratulations! Thanks! Each question had a unique "light bulb" moment, which made the set a pleasure to work on. Thanks for all the effort in crafting both the problems and the solutions; the set is deservedly popular. :)
Log in to reply
Thank you so much, lol, it's a relief to see that a decent number of people enjoyed this set, I did work very hard on it to make all the problems unique. When you think about it, there is no direct benefit to posting original questions on brilliant. The only thing that you get from it is the satisfaction of knowing that someone else took their time to solve your problem and they enjoyed it. That's one of the greatest feelings one can get.
Log in to reply
@Trevor Arashiro – Yes, knowing that you've created a problem that others enjoy working on is the most fulfilling experience on Brilliant. It's satisfying to write a solution (to an already posted problem) that is appreciated as well, of course, but I find the process of crafting a problem more engaging.
1/(golden ratio)^3. Notice that as you zoom in on the right corner, all the figures will be similar.
using trigonometry
p
n
+
1
p
n
=
p
n
p
n
−
1
sin36 sec18.
sec18 and sin36 can be found in terms of cos 36.
sec 18 sin 36 comes out to be ( -1 +
5
)/2.
hence ratio is
(
−
1
+
5
)/2)^3.
We notice a bunch of 3 6 − 3 6 − 1 0 8 triangles; in particular, P k P k + 1 B is a triangle of this type.
We also know, from our repertoire of not really useful knowledge, that the ratio of the shorter side to the longer side of a 3 6 − 3 6 − 1 0 8 triangle is φ 1
With this in mind, it is easy to see that P k P k + 1 = φ k + 2 2 0 1 5
Finally, this means P 6 P 7 P 9 P 1 0 = φ 8 2 0 1 5 φ 1 1 2 0 1 5 = φ 3 1 = ( 2 − 1 + 5 ) 3 so our answer is 1 × 5 × 2 × 3 = 3 0