Angle Trisectors Of A Right Triangle
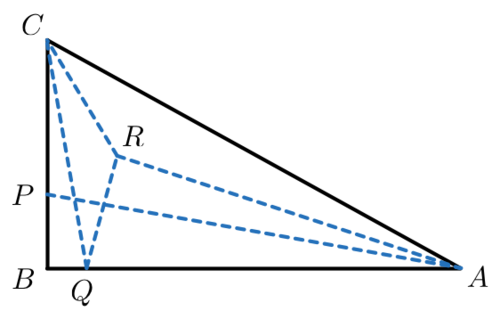Triangle
A
B
C
has angles
∠
A
=
3
α
,
∠
B
=
9
0
∘
and
∠
C
=
3
γ
. Let
P
be a point in segment
B
C
such that
∠
P
A
B
=
α
, and
Q
be a point in segment
B
A
such that
∠
Q
C
B
=
γ
. Let
R
be a point within the triangle such that
∠
R
A
C
=
α
and
∠
R
C
A
=
γ
. If
∠
Q
R
C
=
1
4
2
∘
, what is the measure (in degrees) of
α
?
The answer is 22.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Can you elaborate on the last line, how did you deduce that 2 x gamma = 16 ??
Quite different solution:
Looking at triangle C Q R , we have that γ + ∠ C Q R + 1 4 2 = 1 8 0 . There we get ∠ C Q R + γ = 3 8 which is equivalent to ∠ C Q R = 8 + α since α + γ = 3 0 .
Now, looking at triangle A R Q , we see that ∠ A R Q = 6 8 , and therefore ∠ R Q A = 1 1 2 − 2 α .
Applying the trigonometric form of Ceva's theorem to triangle A C Q , we get sin ( 1 1 2 − 2 α ) sin ( α + 8 ) sin ( α ) sin ( 2 α ) = 1
This is equivalent to cos ( 2 α − 2 2 ) 2 sin ( α + 8 ) cos α = 1
From here, it's not hard to prove that α = 2 2 satisfies the equation above.
Log in to reply
nice, this has perfect explanation, thank you.
how can u get angle ARQ = 68?
Log in to reply
Let S be the intersection of C R with A B . S is between A and Q . Since ∠ Q R C + ∠ S R Q = 1 8 0 , you have ∠ S R Q = 3 8 . Now, ∠ A R S = γ + α = 3 0 , hence ∠ A R Q = 6 8 .
Log in to reply
@Alfredo Saracho – How you u know the value of angle ARS??
Log in to reply
@Ajmal Rissa – ∠ A R S is an exterior angle to triangle A C R . The non-adjacent angles are ∠ R A C and ∠ A C R which are α and γ respectively. Thus ∠ A R S = α + γ = 3 0 .
where did 8 come from
Log in to reply
γ = 3 0 − α , so, when you substitute it in ∠ C Q R + γ = ∠ C Q R + 3 0 − α = 3 8 , well... you get that 8 , Is this what you mean?
gamma + alpha equals 30. Put value of gamma to get expression in alpha.
Assume: D=QR x BC => ACD is right triangle at A => ∠ C D R + ∠ R C D = 1 8 0 − 1 4 2 = 3 8 = > 2 γ + ∠ R D C = 3 8 = γ + α + 8 = > ∠ R D C = α − γ + 8 = α = > γ = 8 , α = 2 2
Log in to reply
what is mean by D=QR x BC
This explains it. Thank a lot.
Why is ACD a right triangle? And why is RDC equal to Alpha? please use words in your work.
Where is D in the figure???
I get the answer of alpha = 11 and gamma = 19. Based on your value, BAC will be larger than BCA and the total angle of AQRC would be more that 360.
Is the angle QRA not 90??
No unique solution The solution only satisfy Alpha + Gamma= 30 That is to say. 22 & 8 is not the unique solution Take 21 & 9. This is also a solution. Also 20 & 10. Give a third solution etc....
does D=RQ X BC means intersection of RQ and BC is D ?
First we note that since triangle ABC is a right triangle, we have
3 α + 3 γ = 9 0
Therefore
α + γ = 3 0
This implies that the angle CRA = 180 - 30 = 150.
Now, let S be the point of intersection of AP and CQ. Looking at triangle CSA we have angle CSA = 180 - 2 (30) = 120. Also in triangle CSA, point R is the intersection of its angle bisectors. Therefore angle CSR = ASR = 60 degrees. This also implies that angle ASQ = 60 degrees. Now comparing triangles ARS and AQS, it is evident that the two triangles are congruent by a common side and two angles.
As a result of congruency, SR = SQ, i.e. triangle SRQ is isosceles, and therefore
angle SQR = 1/2 (180 - 120) = 30 degrees.
Now looking at triangle CRQ, the sum of its angles is 180, therefore,
1 8 0 = γ + 1 4 2 + S Q R = γ + 1 4 2 + 3 0
From which it follows that
γ = 8 degrees
which implies
α = 3 0 − γ = 3 0 − 8 = 2 2 degrees
simply brilliant! thank you from Spain.
I did exactly the same.
Is csa even a triangle
S is a point of intersection of AP and QR.
Triangle P R Q is one of the Morley's triangles ⇒ ∠ R S A = 9 0 .
3 α + 3 γ + 9 0 = 1 8 0 ⇒ α + γ = 3 0 .
∠ C R A = 1 8 0 − ( α + γ ) = 1 5 0 .
∠ Q R A = 6 8 .
∠ R A S = α = 2 2
Great observation about Morley's triangles. That was part of the motivation for this question!
Nice solution ⌣ ¨ .
<ARC= 168 Using sine formulas In Triangle CQR: / frac {CQ} {Sine 142} =/ frac { RQ} {Sine Y} In Tr.. AQR: / frac {RQ} {Sin2x} =/ frac { AQ} {Sin 68} In Tr... ACQ: / frac {AQ} {Sin 2y} = / frac {CQ} {Sin 3x}
Eliminating AQ, CQ, and RQ, we get / frac {Sin 142} {Sin 68} = / frac {Sin 3x/times Sin y} {Sin 2x/times{ Sin 2y}
now Cos y= Cos(30-x) = 0.866 Cos x + 0.5 Sin x Hence 0.664 =/ frac {3 - 4/times Sin x^ {2}} { (0.866 Cos x + 0.5 Sin x)/times 4 Cos x} This leads to a quadratic equation involving Sine x^ {4} and Sine x^ {2}... (convert Cos x into Sine x) After the math, we get Sine x^ {2} = 0.75 or 0.14039 Sine x = 0.8660 or 0.3747 x= 60 degrees or 22 degrees Since x+y = 30 degrees x=22 degrees
Brilliant.
The ultimate solution .
Let S be a point on CQ produced such that angle SRQ=8, then angle SRA=60. Also CRS=CRA=150, SCR=ACR=gamma and CR common therefore CSR and ACR are congruent triangles. then SR=AR therefore SRA is an equilateral triangle. Let CR produced meet AS at T, it is east to see that RT is the bisector of SRA angle. Therefore CST and CBQ are similar triangles. then we get angles ASQ=CQB=SQA, then AQ=AS=AR, i.e triangle ARQ is isosceles. angles AQR=ARQ=68, then we get 2alpha+68+68=180, which implies alpha=22.
∠ C R A = 1 8 0 − ∠ R C A − ∠ R A C = 1 8 0 − ( 3 9 0 ) = 1 5 0 = > ∠ Q R A = 3 6 0 − 1 4 2 − 1 5 0 = 6 8 Assume: D=RQ x BC => ACD is right triangle at A and ∠ B D Q = α = 3 ∠ A D B = > ∠ R Q C + ∠ R C Q = 2 γ + α = 3 8 = > γ = 3 8 − 3 0 = 8 = > α = 2 2