Angles in a Circle

Let ∠ A B C = x , ∠ B C D = 2 x , and ∠ C D E = 3 x . If ∠ B A E is 9 0 ∘ , what is the angle of ∠ A B C in degrees?
The answer is 11.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
But that makes angle BCD = 0 which is 2 x = 2 5 . Clearly 0 = 2 5
Log in to reply
The goal was to find the value of x and those conditions are given. I made a solution that ignores the angle of ∠ B C D . That angle would be equal to 2 2 . 5 , which is 2 x , if the conditions were reverted back to their original state. Changing the angle of ∠ B C D (as long as the other important angles remain unchanged) doesn't affect the value of x .
Log in to reply
I don't quite fully understand. Since no other measurements are provided it should be invariant, isn't it?
Log in to reply
@Mahdi Raza – @Kaizen Cyrus , I agree with @Mahdi Raza . Although simplifying the diagram is a common technique in solving Geometry problems, it doesn't work if you have to sacrifice the rules that were stated in the problem. Because your solution doesn't follow one of the rules in the problem, it must be invalid.
Log in to reply
@Ved Pradhan – If ∠ B C D = 2 x , it would work. If ∠ B C D = 2 x , it would still work. The value of x isn't reliant on said angle.
The angle < CDE never changes no matter where point D lies on the circumference. Like the animation shows, when the two angles meet they form a 45° angle. The rest is self explanatory.
PS: in this case angle < BCD is irrelevant.
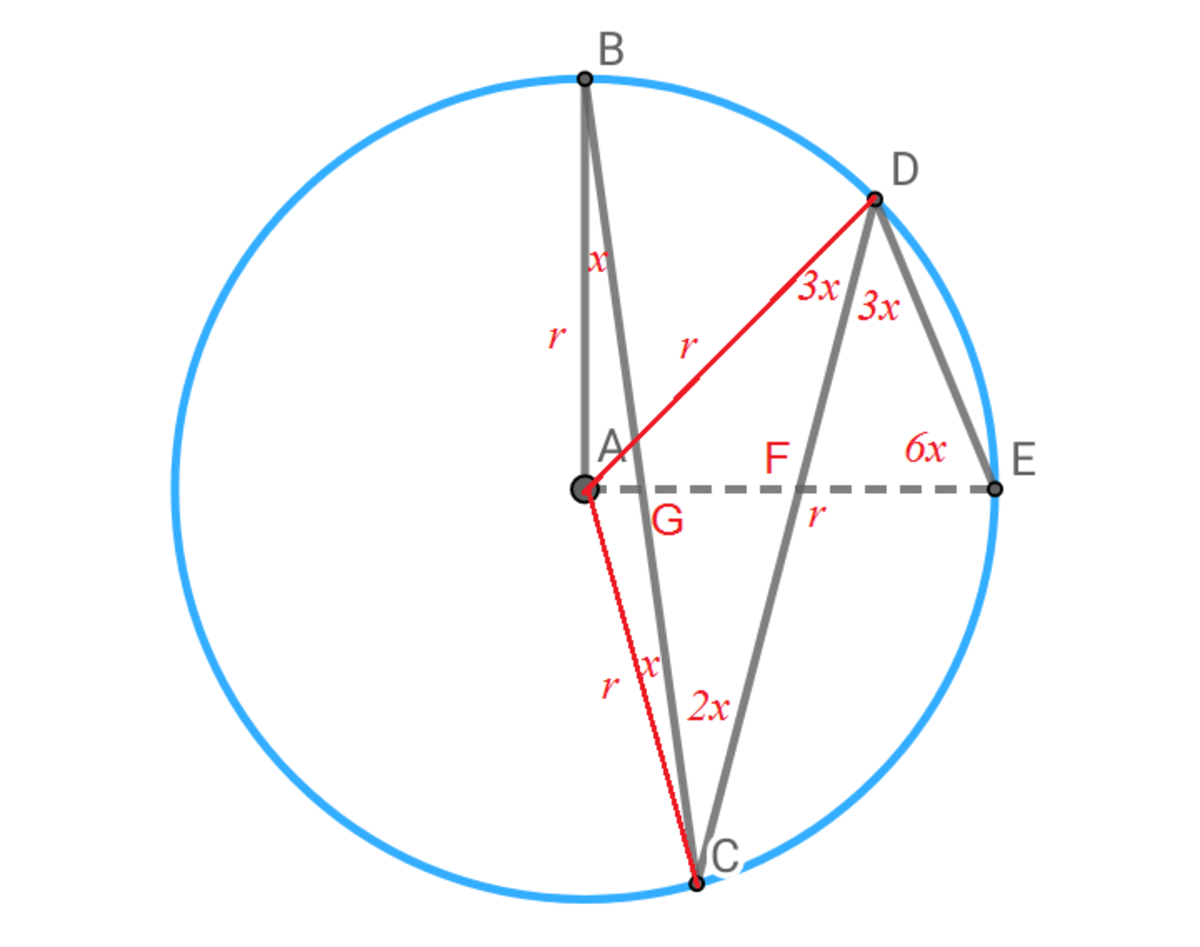
Let the radius of the circle be r . Then we note that △ A B C is isosceles and ∠ A C B = ∠ A B C = x and ∠ A C D = 3 x . Similarly, △ A C D is isosceles and ∠ A D C = ∠ A C D = 3 x . Again △ A D E is isosceles and ∠ A E D = ∠ A D E = 6 x .
Let A E intersect C D and B C at F and G respectively. Then ∠ C G F = ∠ A G B = 1 8 0 ∘ − 9 0 ∘ − x = 9 0 ∘ − x . Similarly, ∠ D F E = ∠ C F G = 1 8 0 ∘ − ( 9 0 ∘ − x ) − 2 x = 9 0 ∘ − x . Then we have for △ D E F :
∠ F D E + ∠ D E F + ∠ D F E 3 x + 6 x + 9 0 ∘ − x 8 x ⟹ x = 1 8 0 ∘ = 1 8 0 ∘ = 9 0 ∘ = 1 1 . 2 5 ∘
Join B E . Then ∠ A B E = 4 5 ° (since △ A B E is right-angled isosceles, with the right angle at A ). So, ∠ C B E = 4 5 ° − x .
Standing on the same arc C E , the angles ∠ C B E and ∠ C D E are equal. So 4 5 ° − x = 3 x ⟹ 4 x = 4 5 °
⟹ x = 4 4 5 = 1 1 . 2 5 ° .
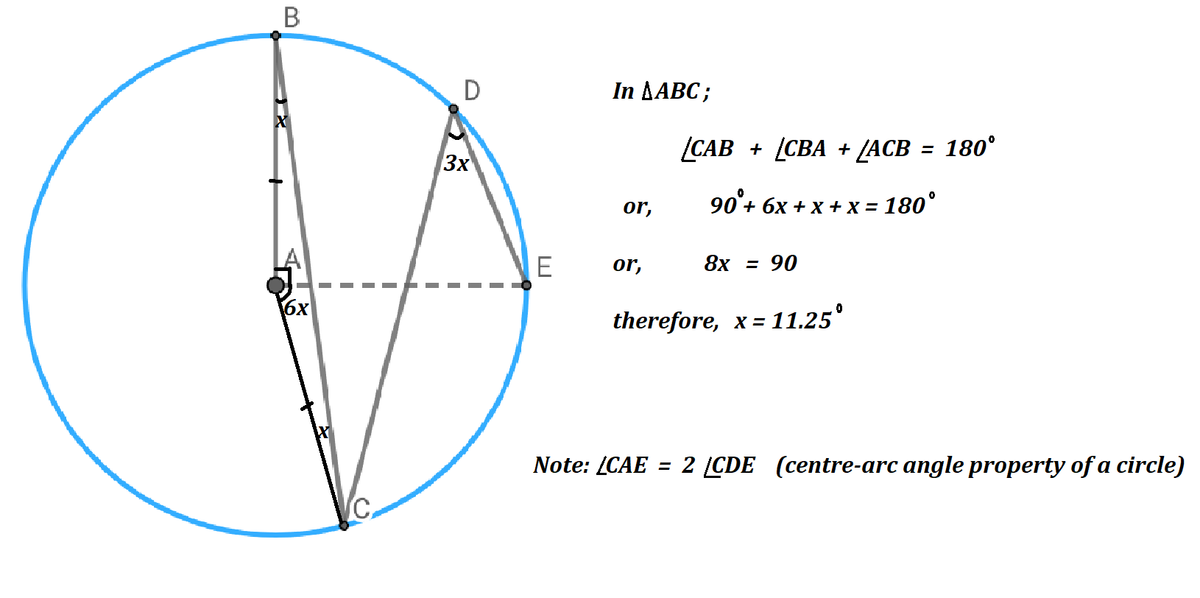
Inscribed Angle Theorem (the reason why ∠ C D E doesn't change measurement in the animation.)