Angles in an equilateral pentagon
Let A B C D E be an equilateral convex pentagon such that ∠ A B C = 1 3 6 ∘ and ∠ B C D = 1 0 4 ∘ . What is the measure (in degrees) of ∠ A E D ?
Note: An equilateral polygon is a polygon whose sides are all of the same length. It does not imply that all the internal angles are equal, nor that the polygon is cyclic.
The answer is 164.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Woah, among all these solutions, this is the elementary-est solution. It might be longer than the others but it's the simplest to understand.
Log in to reply
Thanks! Yes it is a little long, though I tried to make it shorter by skipping a lot of explanations. In questions that just involve angles, my instinct is to try to find a simple angle-chasing solution, and luckily I found one this time. That does make it elementary, in the sense that I just used simple geometric constructions and properties of triangles. I think it's also insightful as it shows some interesting constructions within the pentagon.
Thus ∠ C B D = ∠ C D B = 3 8 and ∠ B A C = ∠ B C A = 2 2 .
I do not understand how you deduced the magnitude of the two angles. From the fact that the triangles are isosceles, one can deduce that the angles are equal, but how does one get their magnitude?
Log in to reply
The sum of the angles in any triangle is 180 degrees. In △ C B D we have ∠ B C D = 1 0 4 , so the sum of the other two angles is 1 8 0 − 1 0 4 = 7 6 . Since the other two angles are equal, they must each be 7 6 ÷ 2 = 3 8 .
It's a similar calculation for △ A B C : ( 1 8 0 − 1 3 6 ) ÷ 2 = 2 2 .
waaaooww, this is magnificent! Elementary, elegant and brilliant! Great!
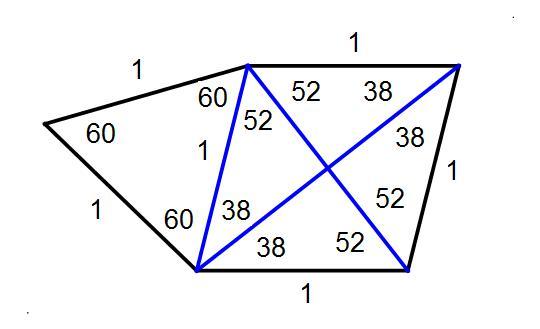
Anytime we have a figure of angles and line segments where there is one point (here point E) that is defined by the intersection of two lines, everywhere else being defined by rational angles, should the angle of that so-defined point is also rational, more likely than not there is a construction involving only figures with rational angles, and it's a matter of finding it. The above graphic shows a combination of a rhombus with an equilateral triangle yielding the same numbers for this equilateral convex pentagon.
There is another equilateral pentagon possible with the same angles
1
3
6
,
1
0
4
, but it's not convex. It's instructive to see how another such construction can be had for this one.
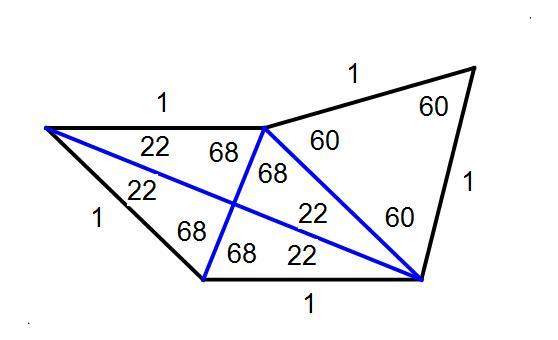
Moderator note:
Regarding the uniqueness of the two solutions given:
Because of the side lengths being fixed and the two given angles, all the points marked red ( A , B , C , and D ) are fixed in relation to each other. That means the only possible variation is the placement of point E . Given a line segment A D , it must form an isosceles triangle A E D where the congruent sides measure the same as those already given; there are only two ways of doing this (corresponding to the pentagon being concave or convex) so there are only two possible solutions.
Oh wow, tbh I didn't realize it was an equilateral triangle on a rhombus.
I could have guessed it given that those angles summed up to 2 4 0 ∘ .
Log in to reply
Calvin, it's a kind of a conjecture that I have is that whenever we have a figure with all rational angles, including one unknown rational angle, which cannot be determined by angle-chasing, then there exists some kind of a construction involving rational angles that makes the determination. In other words, "if the solution looks simple, usually there's a reason why it's simple". See my twisting a prism problem about that, which is why I decided to publish it.
So far I haven't yet found a counterexample of this, i.e., an unknown rational angle is found only by fairly strenuous means involving things like trigonometry or coordinate geometry, where the "nice" number just pops up for no apparent reason.
Let me look at Gu's solution now.
What is the significance of the two angles summing up to 240? can anything be referred?
The problem talks about a convex pentagon, so the second drawing, although interesting, is irrelevant.
Log in to reply
Yes, you are right, llan, it is totally irrelevant.
Log in to reply
Is it really irrelevant? If we construct a solution for the convex case we might still need to prove this is unique.
Log in to reply
@Malcolm Rich – Given 2 points with a distance between them less than 2, then there are only 2 other points that have distances of 1 from both such points. So, I don't see how those two cases described aren't unique. But, of course, the constructions or proofs of either aren't unique, which is another matter.
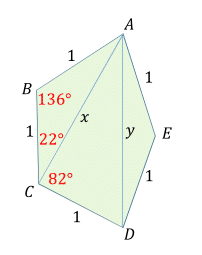
We can arbitrarily set the length of the side as 1 and define x = A C and y = A D .
From triangle A B C using the law of cosine we get x 2 = 1 + 1 − 2 × c o s ( 1 3 6 ∘ ) = 3 . 4 3 9 , x = 1 . 8 5 4 .
△ A B C is isosceles, so ∠ A C B = 2 1 × ( 1 8 0 ∘ − 1 3 6 ∘ ) = 2 2 ∘ . This leaves ∠ A C D = 1 0 4 − 2 2 = 8 2 ∘ .
From triangle A C D we get y 2 = x 2 + 1 − 2 × x × c o s ( 8 2 ∘ ) = 3 . 9 2 3 . y = 1 . 9 8 1 .
Another use of law of cosines, this time to get angle α = ∠ A E D from triangle A E D :
c o s ( α ) = 2 1 + 1 − y 2 = − 0 . 9 6 1 , α = 1 6 4 ∘ .
If one were interested in the rest of the angles:
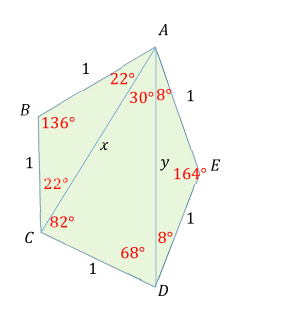 From the isosceles triangle
A
E
D
it is easy to get the two
8
∘
angles, and in the triangle
A
C
D
we know two sides,
x
and
y
and the angle
D
C
A
=
8
2
∘
. Using law of sines, we get
∠
C
D
A
=
6
8
∘
and from the total for the triangle the final one.
From the isosceles triangle
A
E
D
it is easy to get the two
8
∘
angles, and in the triangle
A
C
D
we know two sides,
x
and
y
and the angle
D
C
A
=
8
2
∘
. Using law of sines, we get
∠
C
D
A
=
6
8
∘
and from the total for the triangle the final one.
After all the trigonometries, I'm surprised that the answer is still an integer. I believe Calvin curated the numbers carefully.
Is it possible to find other angles, though?
Log in to reply
Finding the remaining angles is not difficult, and I have added them to the bottom of the solution.
Also, note that for a regular Pentagon, the sum of all the internal angels is 180 * (5-2) = 540.
Log in to reply
The sum of internal angles holds for any pentagon, as long as it is not self-intersecting, but it doesn't give us the angles C A D and A D C individually, only their sum. So law of sines is still needed. That sum could give us the last angle, once the other is known, of course.
Oh, very nice. Much neater than the solution that I had. (As such, I might have over judged the difficulty of the problem. I've adjusted the position of this problem, so those who view this quiz subsequently will see it as the 2nd question, instead of the 5th.)
Technically/ideally, the values of x and y should be left in exact form and not approximated out. That shouldn't be too tricky to work with.
Exactly how I did it (on the third try). If you use a calculator that stores numbers so that you don't have to round anything, the answer is exactly 164 too, no rounding necessary. I figured that might happen since the question mentions nothing about rounding, but it was still cool that it happened that way.
Log in to reply
Yeah, I cheated too using your reasoning and got the same answer. What's left is able to prove that 164 is the EXACT answer...
Instead of using trigonometry i used just geometric techniques.just see that since all sides of bcde are equal so 104 + 76 equals 180.so angle Eba is 136-76=60.since opposite angles are equal in rhombus bcde , the angle Deb is 104.so the total angle and is 104+60=164 degrees.simple and elegant.!!
Log in to reply
Distance BE is not given, so you don't know to start with that BCDE is actually a rhombus. It turns out to be in this case, as is shown in the second solution below, but if the angles were chosen slightly differently, your solution would not work.
A method that I like to use on these difficult looking geometry problems is to see what happens when we try to force something pretty.
WLOG, assume that all of the sides are of lenght 1 unit, since we can scale the figure without changing the angles.
We can look at what happens when we form a segment parallel to C D with length 1 starting from B and connecting it to some other point B ′ such that B B ′ passes through the figure given. Therefore ∠ C B B ′ = 7 6 ∘ , which leaves ∠ A B ′ B = 6 0 ∘ . Note that this point is unique under these conditions.
Now, let's connect point B ′ to A . This will result in an isosceles triangle; B B ′ = A B = 1 with an included angle of 6 0 ∘ , so triangle △ A B B ′ must be equilateral which implies that A B ′ = 1 as well.
Now, connect point B ′ to D . This must result in a rhombus B B ′ C D , since B B ′ ∥ C D and B B ′ = C B = C D = 1 . This then implies that B ′ D = 1 .
We now have constructed a equilateral pentagon equivalent to that of the figure given with the exception of point E and its connecting segments, since we are unsure of where B ′ lies in comparison to E .
The last thing to consider is how, given points A , B , C , D set up exactly like the figure, can we connect points A and D using two segments of length one? It is fairly straightforward to see that if its possible (our construction proves that it is) there are exactly two ways to connect these points, one of which would result in a convex polygon, the other a concave polygon. This means that our constructed figure will either be the convex one, and thus B ′ lies exactly on E and we have all the information necessary to solve the problem, or the concave one (I'll discuss this case later)
Our constructed diagram gives ∠ A B ′ D = 1 6 4 ∘ , which matches the concavity of the diagram given (all angles are less than 1 8 0 ∘ ) and is then our answer.
If it didn't match the concavity given, ie gave an angle greater than 1 8 0 ∘ , we can then form a rhombus A B ′ D E since all sides are the same. The angle we solved for would then be the 3 6 0 ∘ compliment to the interior rhombus angle, which is the desired angle.
What is your motivation for setting up a parallel line B B ′ ? That seems pretty random to me.
Log in to reply
I think it's just that this is the easiest way to explain the solution. It may not be how the solution was found.
Log in to reply
Correct. Initially I saw that we can divide the yellow angle into the 1 8 0 ∘ compliment of the pink angle, and a 6 0 ∘ angle which screamed equilateral triangle and rhombus. The next step was to show that this construction matched the diagram, which is how my solution came about.
Even if that wasn't the case, (where they lined up exactly) I always try to force something pretty as my first steps towards solving math team geometry problems since usually those questions have quick and elegant solutions that can be arrived at using these new constructions
Actually you don't need to consider the case where your construction doesn't match the concavity. You already showed that △ A B B ′ is equilateral, which means ∠ A B ′ B = 6 0 ; and B B ′ C D is a rhombus, so ∠ D B ′ B = ∠ D C B = 1 0 4 . Therefore ∠ A B ′ D = ∠ A B ′ B + ∠ D B ′ B = 1 6 4 . This proves that you got the convex solution.
By the way, this was a smart way of solving the problem!
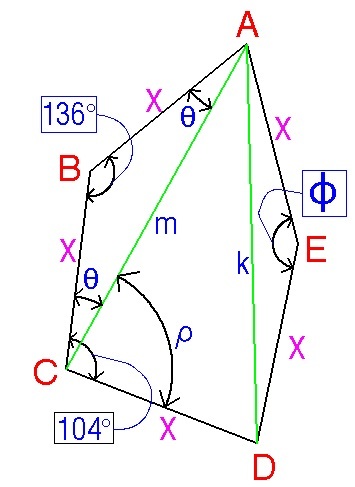
Let x be the side length of the pentagon. Let's consider triangle A B C . By cosine law, we have
m 2 = x 2 + x 2 − 2 ( x ) ( x ) c o s 1 3 6 = 2 x 2 ( 1 − c o s 1 3 6 )
m = x 2 1 − c o s 1 3 6
By cosine law again,
x 2 = x 2 + m 2 − 2 ( x ) ( m ) c o s θ
After some substitution, we get
θ = 2 2 °
Solving for ρ , we get
ρ = 1 0 4 − 2 2 = 8 2 °
Let's consider triangle A C D . By cosine law, we have
k 2 = m 2 + x 2 − 2 ( m ) ( x ) c o s 8 2
After some substitution, we get
k 2 = x 2 [ 1 + 2 ( 1 − c o s 1 3 6 ) − 2 2 1 − c o s 1 3 6 ( c o s 8 2 ) ]
Let's consider triangle A D E . By cosine law, we have
k 2 = x 2 + x 2 − 2 ( x ) ( x ) c o s ɸ = 2 x 2 ( 1 − c o s ϕ )
Equate k 2 and k 2 ,
x 2 [ 1 + 2 ( 1 − c o s 1 3 6 ) − 2 2 1 − c o s 1 3 6 ( c o s 8 2 ) ] = 2 x 2 ( 1 − c o s ϕ )
After simplifying the above equation, we get
ϕ = 1 6 4 °
The quadrilateral BCDE is a parallelogram! Easy since then.
connect points A&B to D as CB=CD so Angle cbd equal to Angle cdb = 38° so < DBA =136-38=98 so cos 38=(BC^2-CD^+BD^2)÷(2BC.BD . ) ~ BD=2BC.cos38 =2k.cos38 at∆ ABD. cos 98=k^2+4.k^2.cos^2 38-AD^2÷2k.2k.cos38 . So AD^2=k^2(4.cos^2 38+1-4.cos 38.cos 98). Ad=1.980536k ,at ∆ AED cosE=(k^2+k^2-1.980536^2.k^2)÷(2k.k) so cos E= -.96126169 so Angle E=164°.
Ah thanks. I was able to follow through this solution once I've connected all the lines in the image.
On the other hand, you have only shown that the angle E is approximately 164, but can you show that the angle is exactly 164?
My original approach measured the length of AD by reference to sines and cosines of the known external angles using BC as the x-axis. The vector AD is (1+cos44+cos76,sin76-sin44) and summing squares and simplifying gives the length to be [2x (1+cos 44 + cos 76)]^.5. Let's call this y.
Then using y^2 = 2 - 2cosE means that cosE = -cos44-cos76. Or Cos (180-E) = Cos44 + Cos76. The graphical representation of this gives us the same equilateral triangle noted elsewhere which produces the answer of 164.
Make a line BE such that CDEB is a parallelogram. Base on the characteristics of parallelogram, Degree of ∠CBE= 180°-104°=76 ∠BED = ∠BCD = 104° So,∠ABE=136°-76°=60° Since it is an equilateral pentagon, So AB=AE. So,∠ ABE=∠AEB=60° ∴∠AED=∠AEB+∠BED =104°+60°=164°
Draw the lines A C and B D . Let's label their point of intersection Q .
Given that all sides of the pentagon are equal, the triangles Δ A B C and Δ B C D are isosceles.
Thus ∠ C B D = ∠ C D B = 3 8 and ∠ B A C = ∠ B C A = 2 2 .
Thus ∠ B Q C = 1 2 0 . Thus ∠ B Q A = ∠ C Q D = 6 0 and ∠ A Q D = 1 2 0 .
Also, ∠ D B A = 9 8 and ∠ A C D = 8 2 .
Draw the line segment B R such that ∠ D B R = 6 0 and R lies on A C .
Similarly, draw the line segment C S such that ∠ A C S = 6 0 and S lies on B D .
Note that Δ B Q R and Δ C Q S are equilateral triangles.
Also note that ∠ A B R = 3 8 and ∠ D C S = 2 2 .
Therefore, the triangles Δ A B R , Δ C B Q , and Δ C D S are all congruent.
Therefore A R = Q S and R Q = S D , so A Q = D Q .
Draw the line E Q . Note that the triangles Δ A E Q and Δ D E Q are congruent.
Therefore E Q splits ∠ A Q D in half, so that ∠ A Q E = ∠ D Q E = 6 0 .
Now let's compare the triangles Δ Q E D and Δ Q C D . They have two pairs of equal sides ( D Q = D Q and C D = D E ), and they have one pair of angles equal ( ∠ D Q C = ∠ D Q E = 6 0 ).
We have a similar situation with the triangles Δ Q E D and Δ Q B A : D Q = A Q , D E = A B , and ∠ D Q E = ∠ B Q A .
However, in both cases the congruent angle is not in between the two congruent sides. So essentially, we have an "ambiguous case" where Δ Q E D is either congruent to Δ Q C D or Δ Q B A . So ∠ Q E D = 8 2 or 9 8 , and hence ∠ A E D = 2 ( ∠ Q E D ) = either 1 6 4 or 1 9 6 .
Of course, we are given that A B C D E is a convex pentagon so that only leaves one possibility: ∠ A E D = 1 6 4 .