Angular width of Refracted Beam!
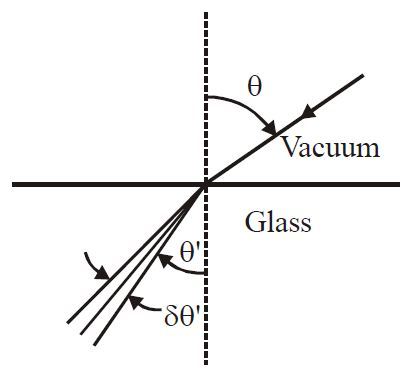 A beam of light has a small wavelength spread
δ
λ
about a central wavelength
λ
. The beam travels in vacuum until it enters a glass plate at an angle
θ
relative to the normal to the plate, as shown in the figure. The index of refraction of the glass is given by
n
(
λ
)
. The angular spread
δ
θ
′
of the refracted beam is given by?
A beam of light has a small wavelength spread
δ
λ
about a central wavelength
λ
. The beam travels in vacuum until it enters a glass plate at an angle
θ
relative to the normal to the plate, as shown in the figure. The index of refraction of the glass is given by
n
(
λ
)
. The angular spread
δ
θ
′
of the refracted beam is given by?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Nishant Rai I think this is a previous JEE problem??? Can you cross check with correct answer?
Log in to reply
I don't know about JEE but this question came in ALLEN All India Open Test 1 (Advanced).
Original Question -
Angular Width of Refracted Beam
Log in to reply
I think there is something wrong with the options given. And I have definitely come across this problem before... Also, if you don't want to solve at all, then you can just put θ 1 = 0 and see the magic!
Log in to reply
@Raghav Vaidyanathan – θ 1 = 0 → JEE Style ! ⌣ ¨
This is 2014 kvpy's sx question and the answer is correct
I don't think the answer given is exactly right, but here is what I got:
From Snell's law:
sin θ 1 sin θ = n ( λ )
⇒ n ( λ ) sin θ = sin θ 1 . . . . . . . . ( 1 )
Taking derivative on both sides:
⇒ ( n ( λ ) ) 2 − sin θ × d n ( λ ) × δ λ = cos θ 1 × δ θ 1 . . . . . . . . ( 2 )
Divide ( 2 ) by ( 1 ) :
⇒ n ( λ ) − d n ( λ ) × δ λ = cot θ 1 × δ θ 1
Neglect minus sign:
δ θ 1 = n ( λ ) tan θ 1 × d n ( λ ) δ λ