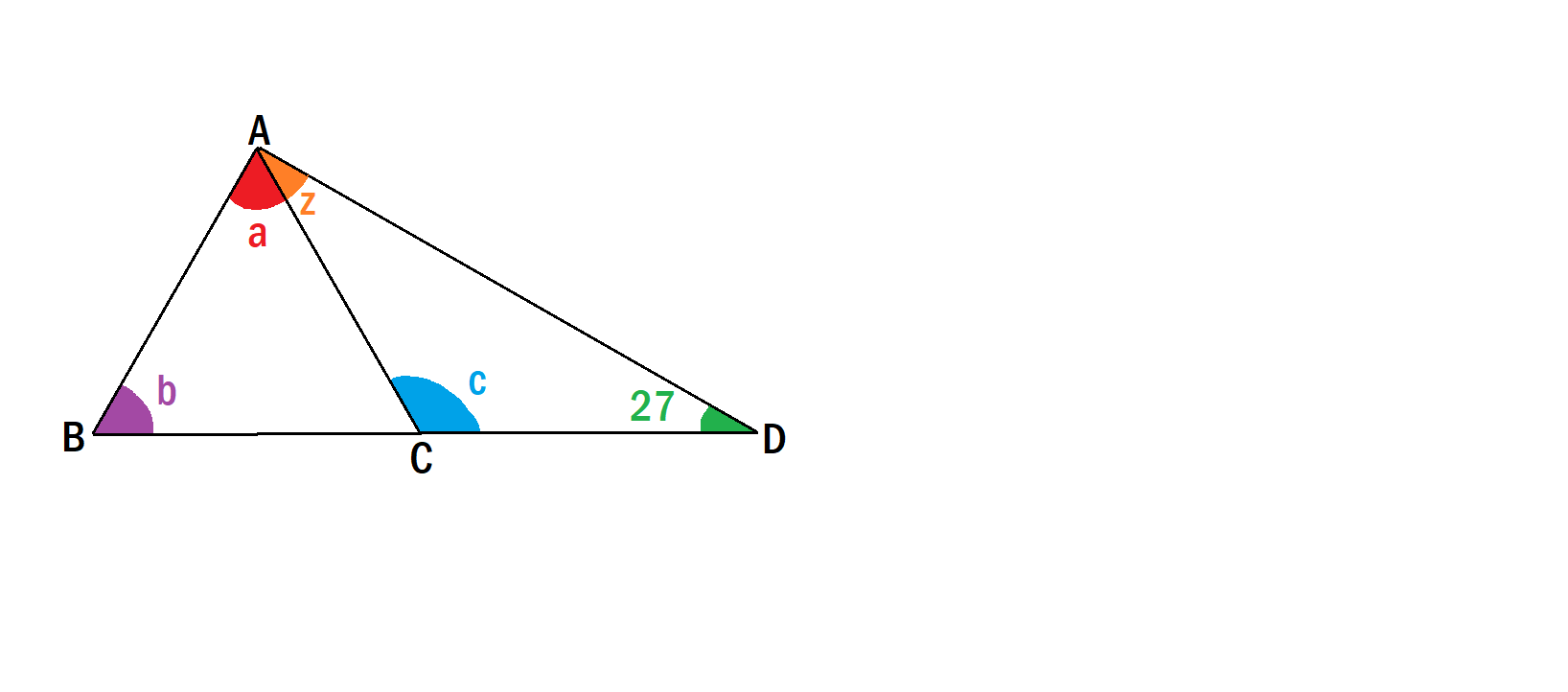
Anlgle Hunters

$\triangle ACD$ is isosceles with $AC=CD$ , therefore $z=27^\circ$ . The sum of interior angles of a triangle is $180^\circ$ , so $c=180-27-27=126^\circ$ . Now, $\angle ACB$ and $\angle c$ are supplementary angles (their sum is $180^\circ$ ), so $\angle ACB = 180 - 126 = 54^\circ$ .

$\triangle ACB$ is isosceles with $AB=AC$ , so $\angle ABC=\angle ACB=54^\circ$ . The sum of the interior angles of a triangle is $180^\circ$ , so $a=180-54-54=72^\circ$ .

Okay, so we already know that angle D is 27 deegres. 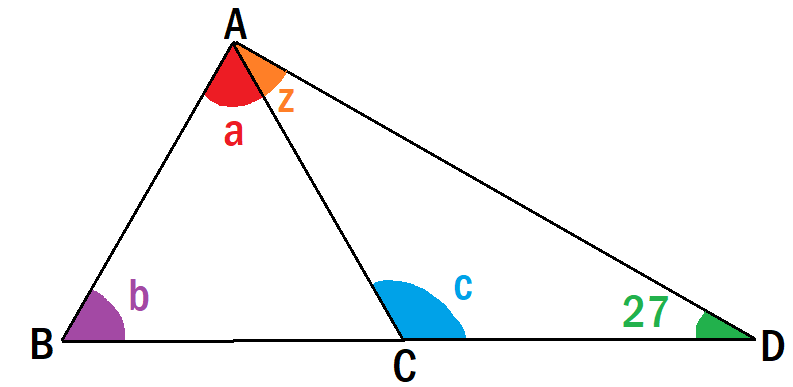We also know that AB=AC=CD. That means that both triangles are isosceles.

If a triangle is isosceles then the two angles opposite the equal sides are equal.

So z=D=27 .

Now that we know z we can easily find c.

As we all know, the sum of a triangle's angles is 180. So:

c=180-(z+D)

180-(27+27)

180-54

*=126. *

Now it's time to find b. In order to find b we have to add another angle, let's name it y.

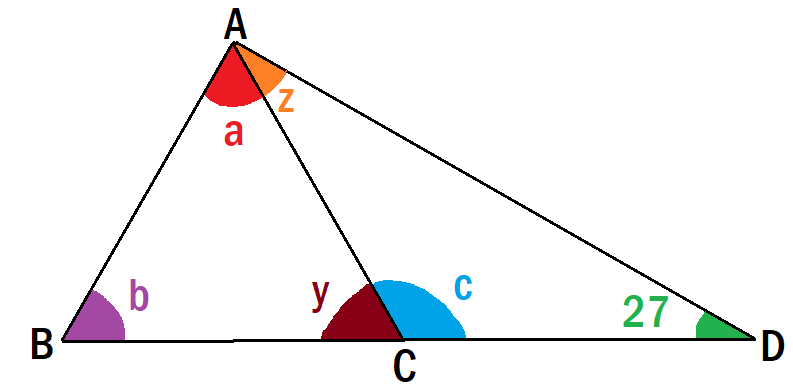
y is supplementary with c. So:

y=180-c

180-126

=54

As we already know, b and y are equal, because the triangle is isosceles.

That means that b=54

Finally, only a is left. As we mentioned before, the sum of a triangle's angles is 180. So:

a=180-(b+y) 180-(54+54) 180-108 =72

OR

a=180-2b 180-54*2 180-108 =72