Another curious identity

Using the identities

$\cos(\alpha) + \cos(\beta) = 2\cos(\frac{\alpha + \beta}{2})\cos(\frac{\alpha - \beta}{2})$ and $\cos(2\theta) = 2\cos^{2}(\theta) - 1,$

this expression can be written as

$\cos(12^{\circ}) + \cos(60^{\circ}) + \cos(84^{\circ}) - \cos(60^{\circ}) - \cos(48^{\circ}) - \cos(24^{\circ}) =$

$\cos(12^{\circ}) + 2\cos(12^{\circ})\cos(72^{\circ}) - \dfrac{1}{2} - 2\cos(12^{\circ})\cos(36^{\circ}) =$

$\cos(12^{\circ})(1 + 2\cos(72^{\circ}) - 2\cos(36^{\circ})) - \dfrac{1}{2} =$

$\cos(12^{\circ})(4\cos^{2}(36^{\circ}) - 2\cos(36^{\circ}) - 1) - \dfrac{1}{2} = -\dfrac{1}{2} = \boxed{-0.5}$

since $\cos(36^{\circ})$ is a root of the polynomial $4t^{2} - 2t - 1.$

To see why this is the case, let $x = 36^{\circ}.$ Then

$3x = 180^{\circ} - 2x \Longrightarrow \sin(3x) = \sin(2x)$

$\Longrightarrow 3\sin(x) - 4\sin^{3}(x) = 2\sin(x)\cos(x)$

$\Longrightarrow \sin(x)(4\sin^{2}(x) + 2\cos(x) - 3) = 0$

$\Longrightarrow -\sin(x)(4\cos^{2}(x) - 2\cos(x) - 1) = 0.$

Now clearly $\sin(x) = \sin(36^{\circ}) \ne 0,$ so we can conclude that $\cos(x) = \cos(36^{\circ})$ is a root of the polynomial $4t^{2} - 2t - 1.$

Brian has submitted a very fine solution. For the sake of variety, let me suggest a solution based on roots of unity; I'm thinking of these cosines as the shadows of the 30th primitive roots of unity, $w$ , on the real axis, with $w=e^{2k\pi{i}/30}$ , for $k=1,7,11,13,...$ .

The sum of these primitive roots of unity is $-1$ ; one can see this with an inclusion/exclusion kind of argument. Adding conjugate pairs, we get what we want: $2\cos(1\times{12^\circ})$ $+2\cos(7\times{12^\circ})$ $+2\cos(11\times{12^\circ})$ $+2\cos(13\times{12^\circ})=-1$ , so that the sum of the cosines is $\boxed{-\frac{1}{2}}$

In general, the sum of the primitive $n$ -th roots of unity is $\mu(n)$ , the Möbius function: it is $(-1)^m$ for a square-free number with $m$ prime factors, and 0 otherwise. Thus $\mu(30)=(-1)^3=-1.$ For $n>2,$ we can generalise our "curious identity" as follows:

$\sum\cos\left(\frac{k\times{360^\circ}}{n}\right)=\frac{1}{2}\mu(n)$ where the sum is taken over all $k$ with $1\leq{k}<\frac{n}{2}$ that are co-prime with $n$ .

Here is ALTERNATIVE SOLUTION that does not (explicitly) rely on roots of unity, but it is mathematically equivalent: "By symmetry", we have $\sum\cos(k\times{12^o})$ $=\sum\cos(k\times{24^o})$ $=\sum\cos(k\times{36^o})$ $=\sum\cos(k\times{60^o})$ $=\sum\cos(k\times{72^o})$ $=\sum\cos(k\times{120^o})$ $=\sum\cos(k\times{180^o})=-1=-\cos(0^o)$ , where the angle runs through the open interval $(0^0,360^0)$ in each case. If we add up Equations 1, 5, 6, and 7 and then subtract 2, 3, and 4, we get our result.

I like doing these types of problems with just trigonometry identities, it's just how I roll. Sometimes you just have to get rather creative to make them work.

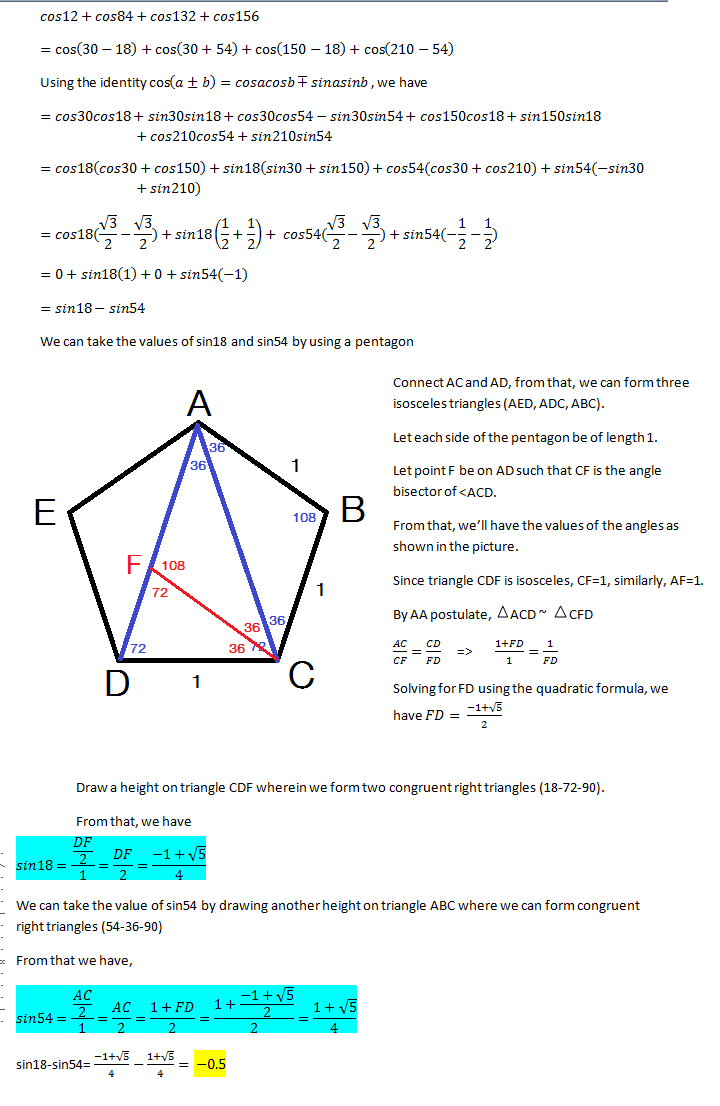
$\color{#20A900}{\cos12}+\color{#69047E}{\cos84}+\color{#20A900}{\cos132}+\color{#69047E}{\cos156}$ $\color{#D61F06}{\cos\theta+\cos\phi=2\cos\frac{\theta+\phi}{2}\cos\frac{\theta-\phi}{2}}$ $=2\cos72\cos60+2\cos120\cos36=\cos72-\cos36$ Note, if you use $\color{#D61F06}{\cos(\frac{\pi}{2}-\theta)=\sin\theta}$ here, you will get $\color{#3D99F6}{\sin18-\sin54}$ , which is the same point Janine Yu got to before using the pentagon.

$\color{#D61F06}{\cos\theta-\cos\phi=-2\sin\frac{\theta+\phi}{2}\sin\frac{\theta-\phi}{2}}$ $=-2\sin54\sin18=-\frac{1}{2}(2\sin54)(2\sin18)$ $\color{#D61F06}{\sin2\theta=2\sin\theta\cos\theta}\Rightarrow\color{#D61F06}{2\sin\theta=\frac{\sin2\theta}{\cos\theta}}$ $=-\frac{1}{2}\frac{\sin108}{\cos54}\frac{\sin36}{\cos18}$ $\color{#D61F06}{\sin(\pi-\theta)=\sin\theta}$

$\color{#D61F06}{\cos(\frac{\pi}{2}-\theta)=\sin\theta}$ $=-\frac{1}{2}\frac{\sin72}{\sin36}\frac{\sin36}{\sin72}=\color{#3D99F6}{-\frac{1}{2}}\space\space\space\Box$