Simulating Dynamics - 1
Difficulty: Moderately hard. Learn about force computation simulation before attempting this.
The simulating dynamics series is original.
Consider a spring block system as I have drawn below:
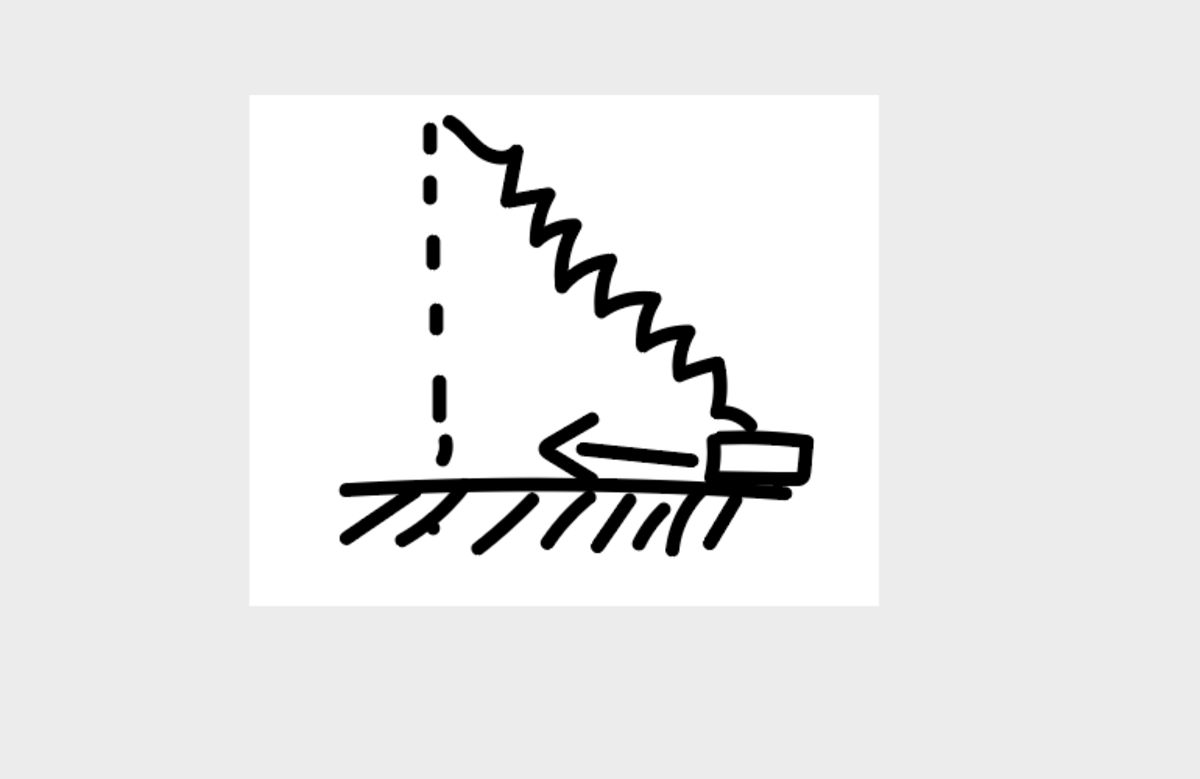
The block of mass 5 kg is connected to a spring which is hinged at the ceiling. The spring constant is k = 2 0 N / m , the natural length is l 0 = 1 meter, and the height between the ceiling and the floor is 1 meter.
The block is initially released 1 0 meters from x = 0 , shown by the dotted line above. There is gravitational acceleration in the − y -direction, g = 1 0 m / s 2
There is a coefficient of friction μ = 0 . 7 , with the opposing force in the x direction (opposing the direction of the velocity) being μ N , N being normal force to the ground.
Find the position of the block x at t = 5 seconds.
Note: the object always slides along the ground.
The best way to do this problem is through computer simulation, once again. The forces interacting are too hard to compute analytically.
The answer is 0.674.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Okay, so what I think is this. The answer to this problem is incorrect. This is because the friction force causes the block to lose kinetic energy. So once the block comes to rest it stays there till the 5 seconds elapse. The correct answer should be − 7 . 1 . See your plot.
@Steven Chase I would like to know your thoughts on this. Once the block comes to rest for the first time, it has dissipated all of its kinetic energy as heat and there exists no other driving force to propel it back into motion. The block finds its equilibrium at that instant.
Log in to reply
Steven got the same answer as me. And he's a much better physicist than me. I think he can provide better insight into your question than me.
Log in to reply
In hindsight, what I said is incorrect. I assessed this problem incorrectly and got the answer wrong. My apologies.
It was a nice one!
Log in to reply
@Karan Chatrath – Ah, thank you for responding nevertheless. I was wondering why the block would come to equilibrium there if the force of the spring was greater than friction at that particular point in time.
Log in to reply
@Krishna Karthik – Yes, that is precisely my mistake. The block still has potential energy when it first comes to rest. The system gets driven back to motion (by the spring force) and dissipates more of its energy until it eventually settles to x = 0 after a long time.
Log in to reply
@Karan Chatrath – It certainly does take a very long time to reach x = 0 . I think if you simulate it for a huge amount of time, it'll eventually stop dead at x = 0 , with negligible vibrations caused simply by the mathematics of the calculation.
My insight is that the ODE of the system has only one steady state I can see, being x = 0 . A similar system would be the pendulum (with drag), which similarly has a 0 steady state.
Log in to reply
@Krishna Karthik – I did solve your problem on the pendulum with drag. Another good one. Indeed, the physics plays out the way you said. Keep posting
I'll try to check the code again; maybe add an energy variable. Thanks for pointing this out.
Log in to reply
No, what you have done is fine. My assessment of the physics is incorrect.
You may be right. When the block comes to rest for the first time, if the horizontal spring force is less than the friction coefficient times the normal force, the block will remain at rest. This assumes that the static coefficient is the same as the dynamic coefficient. I won't have time to play with this again until later today
Log in to reply
Yes, the static is the same as the dynamic coefficient.
I added a few energy variables, and I have found out that the system only loses half of its energy to friction (heat) when it first stops, and still has lots of energy left. I also tried running it for large amounts of time and found that it only fully dissipates all its energy till x = 0 . I have attached the summary to my solution.
When the block comes to rest at x = − 7 . 1 , the rightward horizontal spring force magnitude is ≈ 1 2 2 , and the product of the friction coefficient with the normal force is ≈ 2 3 , so friction can't hold the block still there. Now of course, your argument may hold true at some other point at which the speed of the block becomes zero. But it doesn't appear to be that first stopping point.
Log in to reply
Yes, Karan Chatrath checked back and stated earlier that in hindsight what he had said was incorrect.
Very true, the energy only fully dissipates at x = 0 . Karan already resolved the report.
Thank you for checking. Our discussion following my earlier problem on the exponential wire and this problem have both given me useful insights on modelling friction force.
Fun problem. This sort of problem benefits greatly from a code solution
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
|
My solution is completely numerical, like Steven Chase's. One cannot solve this problem without implementing a numerical solution. The forces involved are too complicated and ever-changing, so it's very hard to do analytically.
My method was to compute the acceleration at each point in time by running a series of force computations. For those who don't understand the theory behind the computer simulation, the forces of the system include gravitational force, spring force, and the frictional force.
The spring force is given by the stretch of the spring and the spring constant:
∣ F s p r i n g ∣ = k ( 1 + x 2 − 1 )
The horizontal and vertical components can be given by multiplying by cos ( θ ) = 1 + x 2 x , sin ( θ ) = 1 + x 2 1
The opposing force to the upward spring force is gravitational force, given by m g .
Now, we need to consider the normal force to the floor, which is the resultant force in the y -axis, given by:
F y = F s p r i n g − F g = 1 + x 2 k ( 1 + x 2 − 1 ) − m g (normal force)
Finally, we can formulate an equation that gives us the force in the x − a x i s :
F x = 1 + x 2 ∣ F s p r i n g ∣ x − μ F y
With this clear in the mind, we can program these forces and compute the total force along the x -axis, thereby determining the acceleration. We can then numerically integrate the acceleration to find the distance travelled given a small time-step. That's the logic behind the computer program.
Graphs produced with matlab:
Here's the python code (using Explicit Euler instead due to slow speed with RK 4):