Simulating Dynamics - 3
Difficulty: quite hard.
Here's another monstrous engineering/classical mechanics exercise. Use simulation once again.
Consider the system shown below, with a block of mass that's connected to a spring on a ramp (with friction):
The coordinate system used is Cartesian. The spring is hinged at point ( 7 , 9 ) and the top-right corner of the mass-block is at the point ( 8 , 8 ) . The bottom of the ramp is at the origin ( 0 , 0 ) .
The force of friction is μ N , with N being the normal force.
The displacement of the block is measured from the top of the ramp to the position of the block, that is diagonally down the ramp. See the diagram. The block is initially at a displacement of 0 . 1 meters from the top of the ramp as shown in the diagram. The Cartesian components are in meters.
It is released from that point at time t = 0 seconds. Find the displacement of the block (from the top) in meters at t = 5 seconds.
Important constants to note:
- The ramp's incline angle is θ = 4 π radians.
- The block's mass m = 8 k g .
- There is ambient gravitational acceleration in the negative y -direction, g = 1 0 m / s 2
- The coefficient of friction of the ramp surface is μ = 0 . 5
- Spring constant: k = 5 0 N / m
- Natural length of spring: 2 meters
The answer is 2.393.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nicely done. I simply plotted the results and later did an energy analysis to see if my results were correct. I used the new set of bases down the ramp, like you did.
Log in to reply
Thanks. Yes, I also just plotted the trajectory, and verified its physical correctness afterwards
@Steven Chase
Sir Hello, Good Morning.
In this problem I am not able to understand this steps
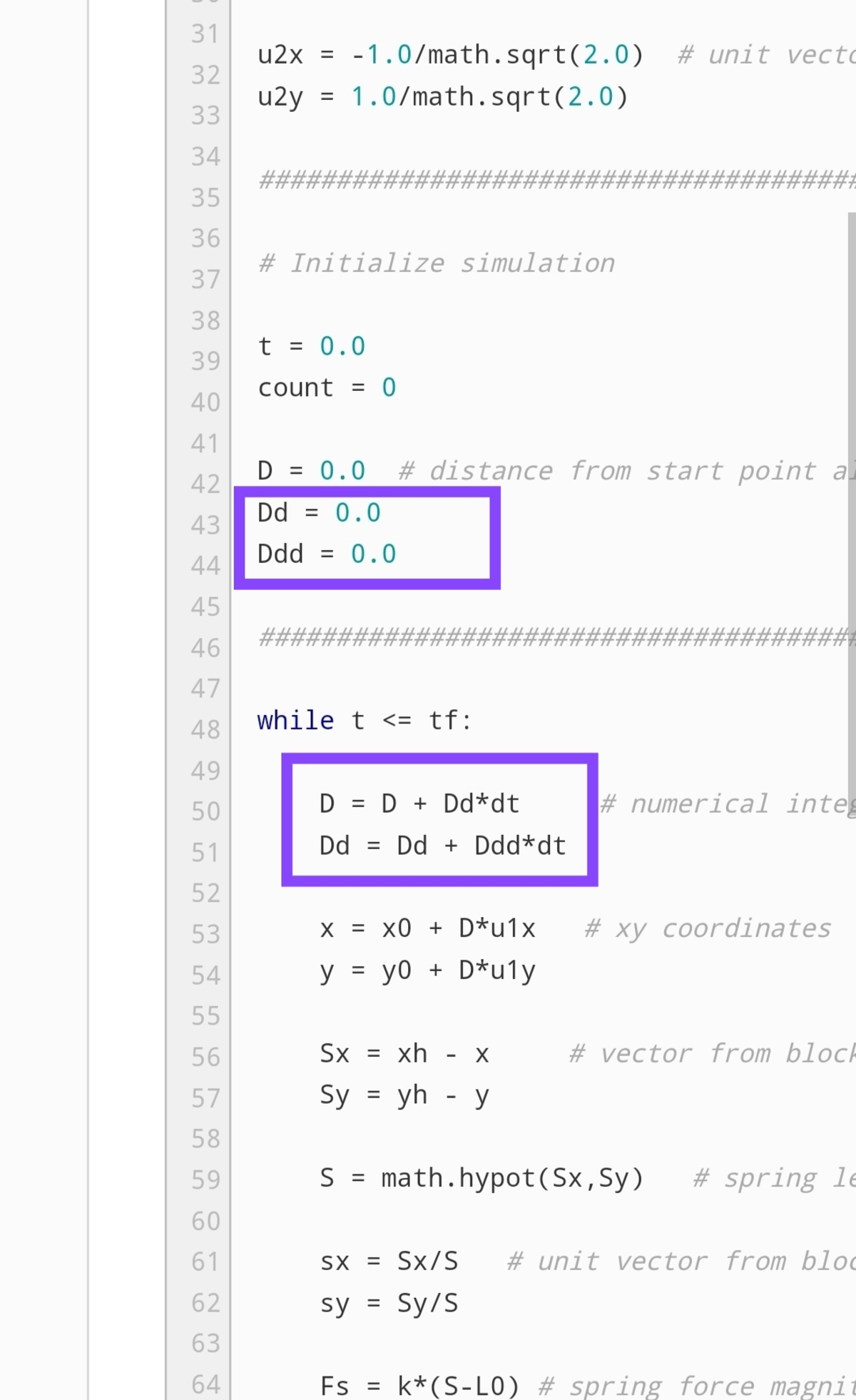
Log in to reply
Those are the first and second time derivatives of the distance down the ramp
Log in to reply
@Steven Chase
sir what is the meaning of D in that blue box and the meaning of h in that green box?
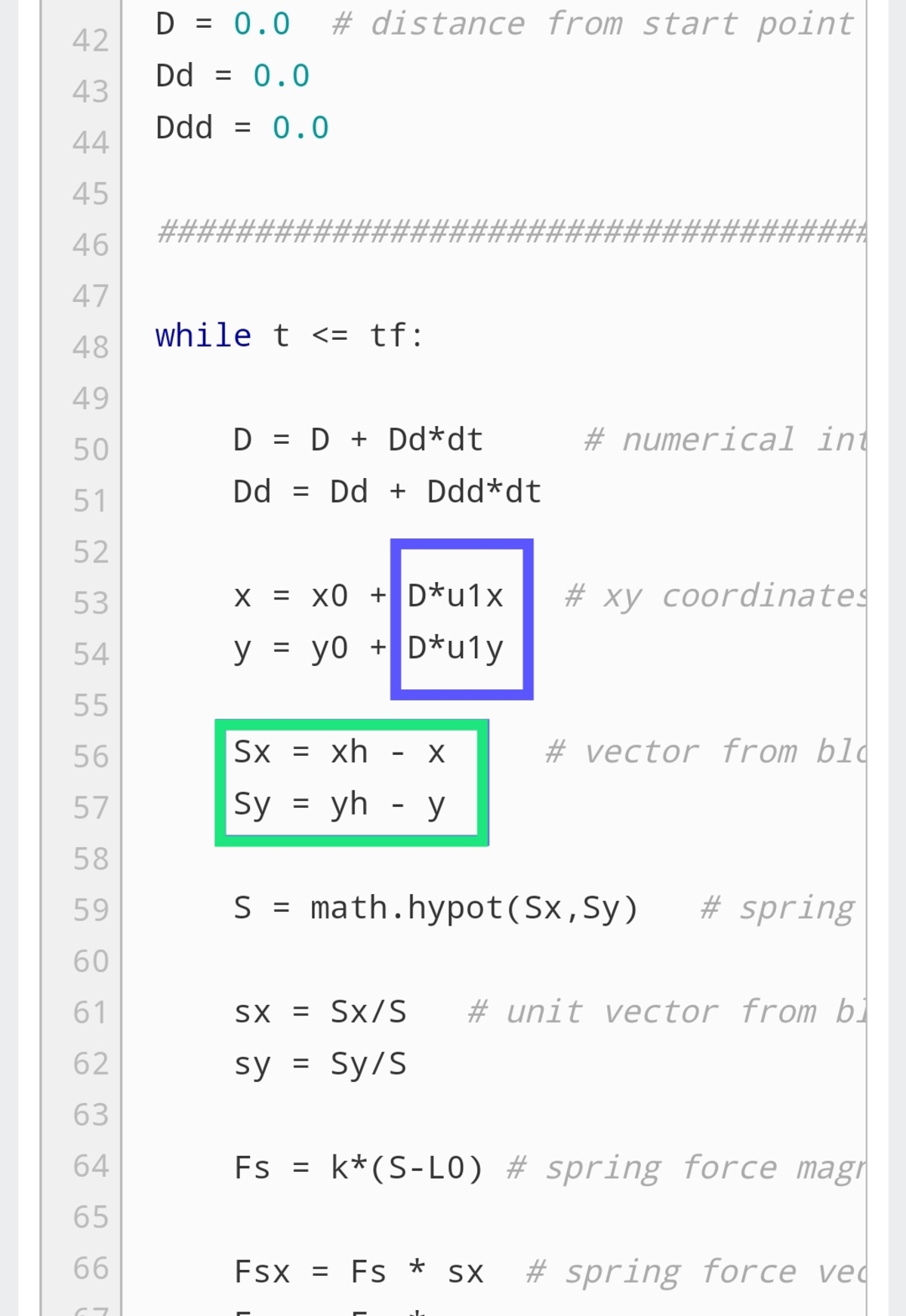
Log in to reply
@A Former Brilliant Member – Let me make a suggestion. This is too difficult a problem to start programming with. Perhaps you could write a program to simulate a parabolic trajectory under the influence of gravity, using numerical integration.
Log in to reply
@Steven Chase – @Steven Chase Sir I will not able to do that, one thing we can do is that first you show me 1 program with answer after that I will do one by myself.
Log in to reply
@A Former Brilliant Member – Don't start programming with physics. Start with the basics, like learning functional programming, how to manipulate strings, calculations, looping, variables, and data types.
@A Former Brilliant Member – I agree with Steven Chase here. This is too difficult to start with numerical simulation.
Yeah; from your doubts you don't seem to have much experience with Python. Learning Python programming is important first. It's actually a pretty simple language to get the hang of.
My approach is completely numerical. The main approach with this kind of problem is to compute the net force and thereby determine the acceleration of the block. The forces acting on the block are:
Gravitational force:
This force makes the block move down the ramp, as well as creates a normal force between the ramp and the block. Let's assume a coordinate system where y is normal to the ramp and x is orthogonal to y (in the slope of the ramp).
F g x = m g sin ( θ )
F g y = − m g cos ( θ )
Spring force:
The spring force components are the most difficult to work out with the new set of bases directions (stated above).
Let the angle the spring makes with the ramp be ϕ .
sin ( ϕ ) = d 2 + 2 2 (where d is the displacement)
cos ( ϕ ) = d 2 + 2 d
The magnitude of spring force:
k s = k ( d 2 + 2 − 2 )
Components:
F s x = − k ( d 2 + 2 − 2 ) cos ( ϕ )
F s y = k ( d 2 + 2 − 2 ) sin ( ϕ )
Frictional force:
The normal force is the net y force, given by:
N = F g y − F s y
So the frictional force is ± μ N (depending on velocity of block).
Total force in x -direction:
F x = F g x + F s x ± μ N
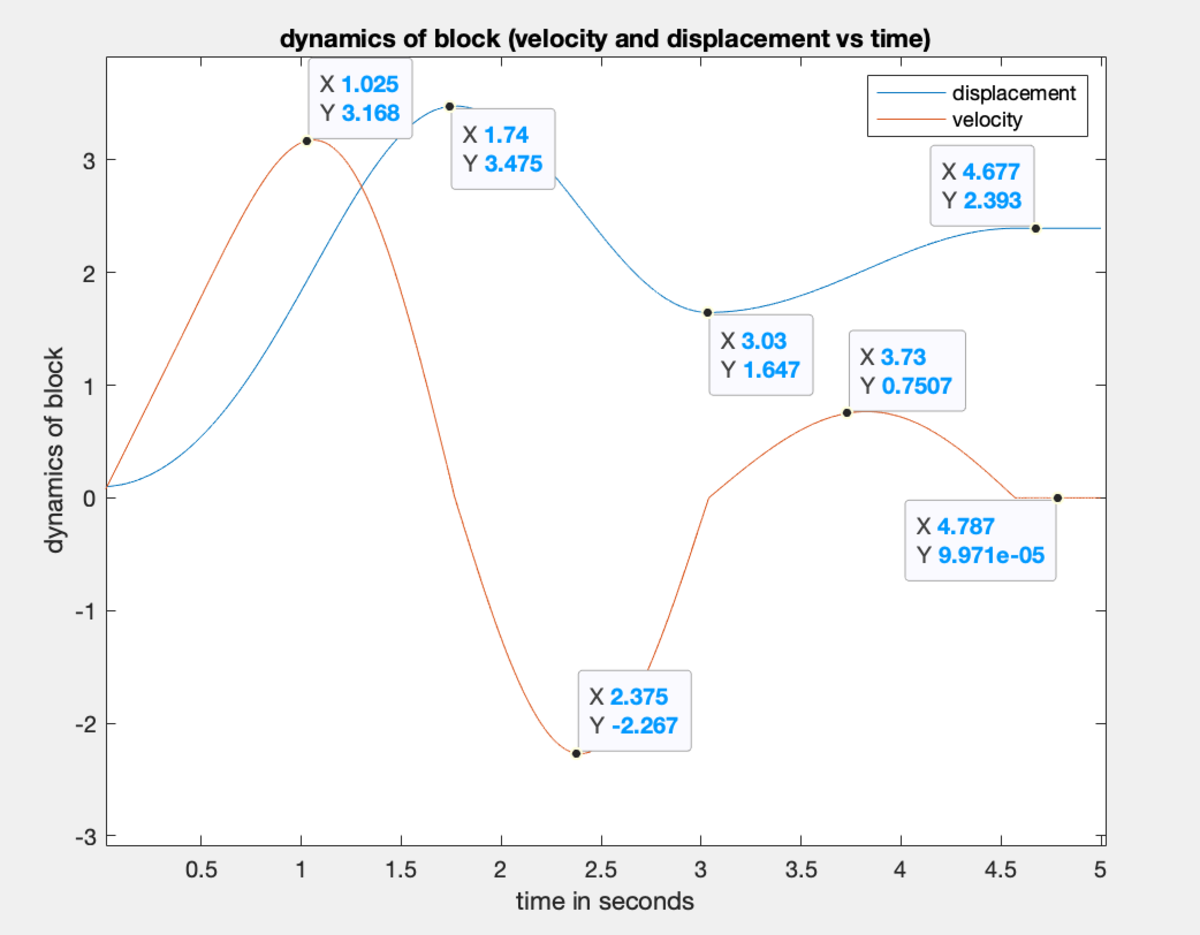
Now, we can code the forces in and simulate the motion of the block. Here's a graph of the displacement of the block:
Here's my code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
|
Nice problem. Just solved it. I was looking at your solution and you have defined:
sin ϕ = d 2
Shouldn't it be:
tan ϕ = d 2
Log in to reply
Oh woops, sorry, I meant sin ( ϕ ) = d 2 + 2 2
Yes, quite right. I'll edit that in a moment.
I like this problem and I have posted a follow up. Hope you enjoy it.
Log in to reply
Ah, I've seen it. I'm going to attempt it soon :) Glad you liked the problem.
Hey, I just solved your problem, nice one.
Fun problem. Simulation code is below. Aside from computing the basic dynamics, the key thing about this problem is to keep track of two different forces:
1) The combined force from gravity and the spring parallel to the ramp
2) The maximum available friction force (equal to the friction coefficient multiplied by the normal force)
Every time the block's velocity becomes zero, you have to check force (1) to see if it is bigger/smaller than force (2). If it is bigger, the motion continues. If it is smaller, the block stays where it is in perpetuity. As it turns out, the block comes to rest at a displacement of ≈ 2 . 4 3 8 at time t ≈ 4 . 6 . It stays there from then on.