Another infinite circuit
Consider a very long (infinite) circuit as shown in the figure. All the resistors have equal resistance. Determine the equivalent resistance
R
A
B
in Ohms
between the terminals A and B if the equivalent resistance between A and C is
R
A
C
=
1
0
Ω
.
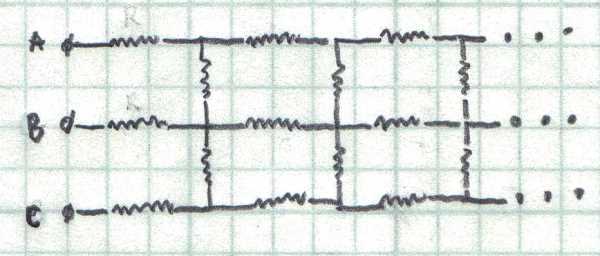
The answer is 8.36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Notifying @Pranav Arora .
Log in to reply
Thank you Sir!
I am still trying to understand the solution. If I can understand it, I will post it as a solution (in an understandable format). :)
The flaw in my approach was that I accidentally removed the lower branch C which gave me an answer of 8.44 which is quite close to 8.36, hence it was marked correct.
Log in to reply
I am really not sure whether what I have done is correct. I obtained the answer as ( 3 5 + 7 ) ( 5 + 1 ) 2 ( 4 1 5 + 9 4 ) which gives the value 8 . 3 7 1 .
Log in to reply
@Karthik Kannan – Your answer is quite close to the correct answer. Can you please show us how you got that expression? :)
Log in to reply
@Pranav Arora – I don't know, I am really not sure...
As we have to calculate the equivalent resistance between A and B the circuit is not symmetric but if we skip one 'rectangular unit' the circuit is again symmetric (just cover the left hand portion and see). Since the circuit is infinitely long removing one unit doesn't make a difference so now the problem reduces to connecting R A C to the first 'rectangular unit'. Now R A B can be found by solving the simplified circuit using Kirchoff's Law (the equations were really complicated as can be seen from the answer obtained).
I feel that my answer is probably wrong and perhaps I was just a bit lucky : )
@Pranav Arora – I know I have explained it really badly. Could you please tell me how to upload an image. Then probably I would be able to explain it better.
Log in to reply
@Karthik Kannan – To post an image, use the following code:

Log in to reply
@Pranav Arora – Sorry, I tried a lot of things but did not succeed. Actually, I do not know the meaning of the terms you mentioned above. Could you please explain.(I am completely new to this)
Log in to reply
@Karthik Kannan – Okay, let me explain with the help of an example. If I use the code (it is not necessary to write anything in those square brackets)

The text I wrote in round brackets is the url or path of the image. Just upload the image on any image hosting website, get the link to the image and paste it in the round brackets.
Output:
![]()
Log in to reply
@Pranav Arora – Thanks!! I think I am getting the hang of it. Now I shall try again...
@Pranav Arora – OK, here goes...
This is our question:

Now as the circuit is symmetric beyond the first 'rectangular unit it can be redrawn as:

which reduces to:

Now on solving the equivalent circuit obtained above we obtain the answer 8.371(It is really quite long-4 equations).
Whew! That was quite a lot of trial and error and hard work (posting the images). Thanks a lot Pranav, for teaching me how to post images. it is very useful!!
Please let me know if this solution is correct/incorrect : )
Log in to reply
@Karthik Kannan – I am not sure. How do you justify removing the middle branch?
Log in to reply
@Pranav Arora – I too am not sure. I argued that since from the second rectangular unit onwards the circuit is symmetric the middle branch can be removed ( I was totally prepared to get the wrong answer but it turned out to be correct, probably due to the small error that the computer accepts).
Log in to reply
@Karthik Kannan – I am still not very convinced though my answer was much erroneous than yours.
Log in to reply
@Pranav Arora – I too am not convinced as the calculations are very bad and generally these questions are not very calculative but have some nice trick.
I think we will just have to wait for someone to post a proper solution.
@Pranav Arora – Listen, Pranav I have been trying to understand a similar question given in that Hungarian website (the same has been shared by Mr. Jon Haussmann above).
I can't understand exactly how the solution works and hence I thought I would discuss it with you.
In that question we have to find the equivalent resistance between points A and C , and between points A and B for the following circuit (which is quite similar to ours):

Here each resistance is of value 1 Ω .
After a lot of back calculation and translation this is what I have been able to make of it:
According to the solution the equivalent circuit can be drawn as follows:

I don't know which point O is but I guess it is the point symmetrically located in the last branch of the circuit (refer the first image that I have put up).
Here R A O = R C O = R and R B O = r .
Thus R A C = 2 R and R A B = R + r
The solution says that as the circuit is infinitely long removing one unit will not change the equivalent resistance.Hence R A C and R A B have been computed as follows:
For R A C they have drawn the equivalent circuit as follows:

Note that middle branch can be taken out due to symmetry.
Thus R A C 1 = 2 R 1 = 2 1 + 2 R + 2 1
For R A B they have drawn the equivalent circuit as follows:

Thus R A B 1 = R + r 1 = 1 + ( 1 + R ) + 1 + r \strut 1 + 2 + R \strut 1 \strut 1 1
What do you think about it? Please share your views.
Log in to reply
@Karthik Kannan – That looks promising indeed. How about posting it as a solution?
Log in to reply
@Pranav Arora – I think I will post it as a solution if I understand it completely. I didn't understand the first step-How can the equivalent circuit be written that way?
Log in to reply
@Karthik Kannan – Yep, I too had trouble with that part. I discussed it with someone and the reasoning was along the following lines. If you measure the resistance between A and B, you will get some value, and by symmetry it will be the same as the resistance between B and C. Also, if you measure the resistance between A and C you will get some other value. So there are only two resistance values that characterize the network. So you can replace the entire network with just those three resistors. But I am still not convinced about replacing the circuit just three resistors.
Log in to reply
@Pranav Arora – Nor am I. But the solution has been written by Péter Gnädig himself so most probably it isn't wrong. But this is the best I could do. We will have to wait for someone to explain it to us properly.
@Karthik Kannan – you cannot remove the middle branch because the circuit is not symmetrical from 2nd unit (it will be symmetrical in R A C not in R A B
R A C = 1 0 Ω ;
denote A , A 1 A 2 ⋯ , B , B 1 B 2 ⋯ , C , C 1 C 2 ⋯ the nodes of the circuit.
Let R every single resistance of the circuit;
R A C = 2 R + 2 R ∣ ∣ R A C , because is a iterate circuit of resistance an for simmetry in the central branches don't flow current;
1 0 = 2 R + 2 R + 1 0 2 R × 1 0 ;
R 2 + 5 R − 2 5 = 0 ,
R = 2 5 ( 5 − 1 ) ;
now for simmetry to calculate R A B , we can observe that the branches C C 1 vanishes, and from B 1 B 2 to the next branches in the
middle of the circuit can be subdivided into two separable circuits with resistances of the middle branches 2 R .
Thus, we have:
if R A B ′ = x R A B = y , :
x = ( 2 R + R ) + R ∣ ∣ x = 3 R + R + x R x ;
This provide:
x 2 − 3 R x − 3 R 2 = 0
x = 2 3 + 3 R ;
y = 2 R + R ∣ ∣ x = 2 R + R + x R x ;
thus:
y = R A B = 5 ( 5 − 1 ) ( 1 + 2 1 ( 3 + 5 3 + 3 ) )
y = 8 . 3 5 2 4 6 7 0 7 ⋯ ≈ 8 . 3 5
[This is a response to a request for a solution.]
I don't have a solution, but I did come across the following link which has a related problem:
http://www.komal.hu/verseny/2001-04/P.h.shtml
It's problem P. 3434. There is a solution, but it's in Hungarian; you should be able to use a web translator to get a decent English translation. It looks like the solution is using a model of a circuit that I'm not familiar with; perhaps you can make better sense of it.