An Inscribed Hexagon
An inscribed Hexagon has sides A F = F E = E D = 4 , A B = B C = C D = 2 . Furthermore, A D E F and A D C B are trapeziums.
If the length of chord A D is n m , where m and n are relatively prime integers, find m + n .
The answer is 43.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Brian, why is <AFD = 1/2 <AOB ?
 Question
Question
Log in to reply
Hi, Guiseppi. ∠ A F B = 2 1 ∠ A O B by the inscribed angle theorem . This theorem was indispensable in solving this problem, (at least the way I went about it).
Great question, by the way. :)
Log in to reply
Check my new problem for a "reality" vindication of that theorem.
Log in to reply
@Guiseppi Butel – Yes, I solved your new problem yesterday as soon as I saw it. It must have been tricky to find all those (large) integer coordinates. :)
Log in to reply
@Brian Charlesworth – Not really, Brian. I just read them off the monitor. I had to figure how to calculate the angles. I used slopes.
Is that the way you did it?
Log in to reply
@Guiseppi Butel – I used the inscribed angle theorem and the Cosine Law, and I calculated the lengths of the sides using the distance formula. I will post a solution tomorrow when my eyes are fresh.
why does 1/2∠AOD=3α
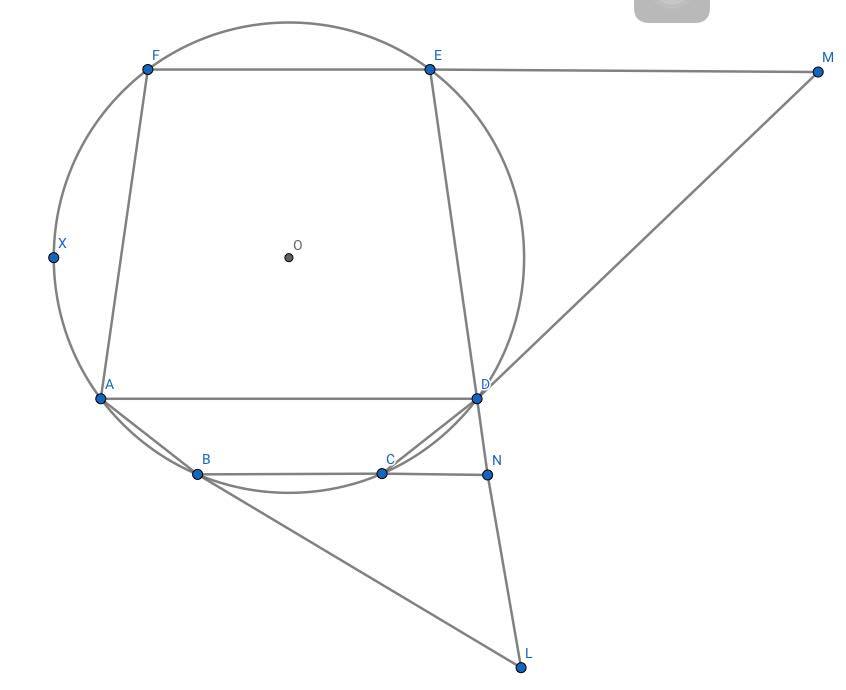
Let F E ∩ D C = M , E D ∩ B C = N , A B ∩ E D = L .
Let L N = y and B L = z
Let E M = a , M D = b
By the Power of a Point, we have
a ( a + 4 ) = b ( b + 2 ) ( 1 )
Notice that Δ E D M ∼ Δ N C D .
So we can have
D N = a 8 , C N = a 2 b
By the Power of a Point, we have
a 8 ( a 8 + 4 ) = a 2 b ( a 2 b + 2 ) ( 2 )
Solving for a and b we get
a = 5 3 2 and b = 5 2 8
So B N = 4 1 5 and D N = 4 5
Notice that Δ A D L ∼ Δ B N L .
So we have z + 2 z = y + 4 5 y ( 3 )
Also by the Power of a Point, we have
( y + 4 5 ) ( y + 4 2 1 ) = z ( z + 2 ) ( 4 )
Solving for y and z we get
y = 5 2 1 7 5 and x = 1 3 7 0
We then achieve A D = 7 3 6
∴ 3 6 + 7 = 4 3 .
I appologize if my latex is not that good.
Also I would like to add that the process of solving the systems of equations was not shown here. I guess I'll leave it to the readers to solve it for themselves.
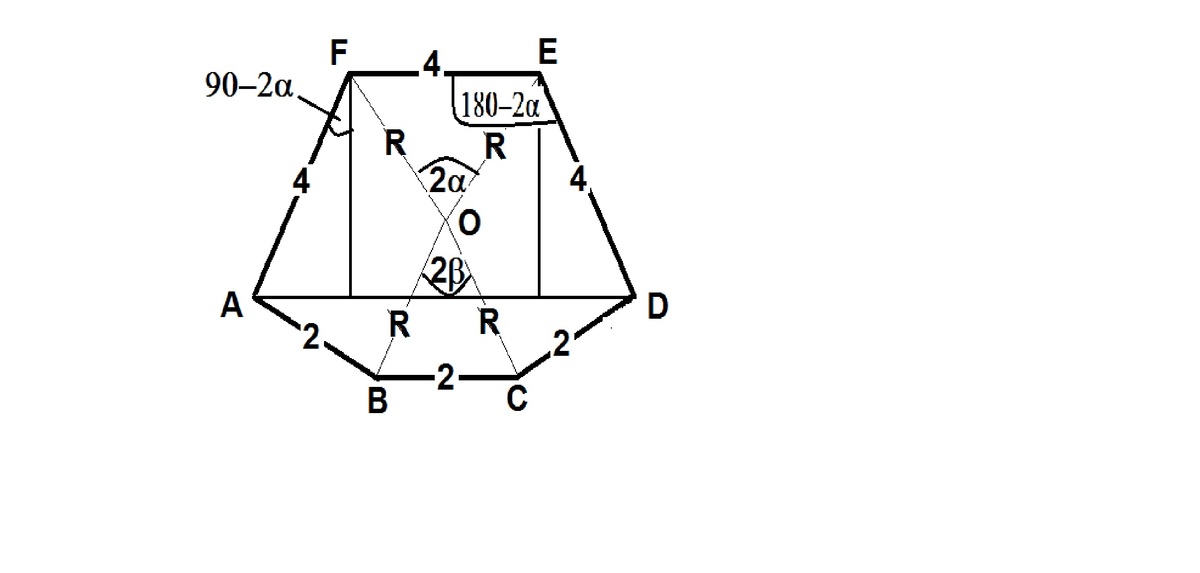
Length of the chord shared by two trapeziums each having three equal sides a & b & being inscribed in a circle is given by the following general formula
A D = a 2 + b 2 + a b 3 a b ( a + b )
As per question, setting a = 2 & b = 4 in above general formula we get
A D = 2 2 + 4 2 + 2 ⋅ 4 3 ⋅ 2 ⋅ 4 ( 2 + 4 ) = 7 3 6 = n m
∴ m + n = 3 6 + 7 = 4 3
 L
e
t
2
α
b
e
t
h
e
∠
s
u
b
t
e
n
d
e
d
b
y
t
h
e
4
u
n
i
t
s
i
d
e
a
t
t
h
e
c
e
n
t
e
r
a
n
d
2
β
b
y
2
u
n
i
t
.
W
i
t
h
R
c
i
r
c
u
m
r
a
d
i
u
s
R
S
i
n
α
=
4
a
n
d
R
S
i
n
β
=
2
,
w
e
h
a
v
e
6
α
+
6
β
=
3
6
0
⟹
α
+
β
=
6
0
.
∴
R
S
i
n
β
R
S
i
n
α
=
2
4
.
⟹
S
i
n
(
6
0
−
α
)
S
i
n
α
=
2
.
S
o
l
v
i
n
g
C
o
t
α
=
3
2
⟹
C
o
s
2
α
=
7
1
.
AD=Projection of AF on AD+ Projection of FE on AD+ Projection of ED on AD.
\
A
D
=
4
S
i
n
{
1
8
0
−
2
α
−
9
0
}
+
4
+
4
S
i
n
{
1
8
0
−
2
α
−
9
0
}
.
A
D
=
4
(
1
+
2
C
o
s
2
α
)
=
7
3
6
=
n
m
.
m
+
n
=
4
3
L
e
t
2
α
b
e
t
h
e
∠
s
u
b
t
e
n
d
e
d
b
y
t
h
e
4
u
n
i
t
s
i
d
e
a
t
t
h
e
c
e
n
t
e
r
a
n
d
2
β
b
y
2
u
n
i
t
.
W
i
t
h
R
c
i
r
c
u
m
r
a
d
i
u
s
R
S
i
n
α
=
4
a
n
d
R
S
i
n
β
=
2
,
w
e
h
a
v
e
6
α
+
6
β
=
3
6
0
⟹
α
+
β
=
6
0
.
∴
R
S
i
n
β
R
S
i
n
α
=
2
4
.
⟹
S
i
n
(
6
0
−
α
)
S
i
n
α
=
2
.
S
o
l
v
i
n
g
C
o
t
α
=
3
2
⟹
C
o
s
2
α
=
7
1
.
AD=Projection of AF on AD+ Projection of FE on AD+ Projection of ED on AD.
\
A
D
=
4
S
i
n
{
1
8
0
−
2
α
−
9
0
}
+
4
+
4
S
i
n
{
1
8
0
−
2
α
−
9
0
}
.
A
D
=
4
(
1
+
2
C
o
s
2
α
)
=
7
3
6
=
n
m
.
m
+
n
=
4
3
Let O be the center of the circle and r the radius. Let 2t be the central angle subtended by the chord lengths of 4. Then sin(t) = 2/r. <AOF = <FOE = <EOD = 2t, so < AOD = 360 - 6t. Then <AOB = <BOC = <COD = 120 - 2t. In triangle AOB, by the Law of Cosines, 4 = 2r^2 - 2r^2 cos(120 - 2t).Cos(120 - 2t) = [sqrt(3)/2] sin(2t) - (1/2) cos(2t). Substituting r =2/sin(t), and simplifying, we derive cos^2(t) = 4/7. From triangle AOD, by the law of cosines, (AD)^2 = 2r^2(1 - cos(6t)). cos(t) = sqrt(4/7) = .755928946, t = 40.89339465, 6t = 245.3603679, cos(6t) = -.416909621. Substituting, (AD)^2 = (56/3) (1.416909621) = 26.44897959, AD = 5.14285714.... . We recognize the decimal part as 1/7. So AD = 36/7, ang m + n = 43. Ed Gray
Referring to the diagram, and letting the center be O , let ∠ A O B = 2 α and ∠ A O F = 2 β .
Now by symmetry 2 α + 2 β = 3 2 π . By the Cosine Law we then have that
( B F ) 2 = 2 2 + 4 2 − 2 ∗ 2 ∗ 4 ∗ cos ( 3 2 π ) ⟹ B F = 2 7 .
Next, note that ∠ A F B = 2 1 ∠ A O B = α and ∠ A B F = 2 1 ∠ A O F = β . So, using the Sine Law on Δ A B F we find that sin ( α ) = 1 4 2 1 and sin ( β ) = 7 2 1 .
Now, we see that ∠ A F D = 2 1 ∠ A O D = 3 α and ∠ A D F = 2 1 ∠ A O F = β . So using the Sine Law on Δ A D F we have that
4 s i n ( β ) = A D sin ( 3 α ) ⟹ A D = sin ( β ) 4 sin ( 3 α ) .
Now sin ( 3 α ) = 3 sin ( α ) − 4 sin 3 ( α ) = 4 9 9 2 1 ,
and so A D = 7 2 1 4 9 3 6 2 1 = 7 3 6 .
Thus m + n = 3 6 + 7 = 4 3 .