Another Locus Problem
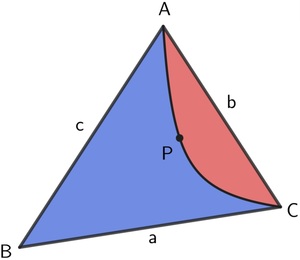
Let P be a point inside a triangle △ A B C such that ∠ P B A = ∠ P C A . The locus of the point P is a curve which divides the triangle into two regions. Find a general expression of the areas of the two regions.
The smaller area when a = 5 , b = 4 , and c = 3 is l − n m ln ( m ) , where l , m , and n are coprime positive integers. Submit l + m + n .
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This is very insightful, thank you!
Could you possibly also post a solution to this problem and it's follow-up ? It'd be very helpful.
Log in to reply
Why don't you post solutions to the problems yourself?
Log in to reply
It is not an original problem. I'm curious to know how to work out the sum.
Log in to reply
@Digvijay Singh – Oh! I think you can indicate the sources in the comment sections at least. It might help others.
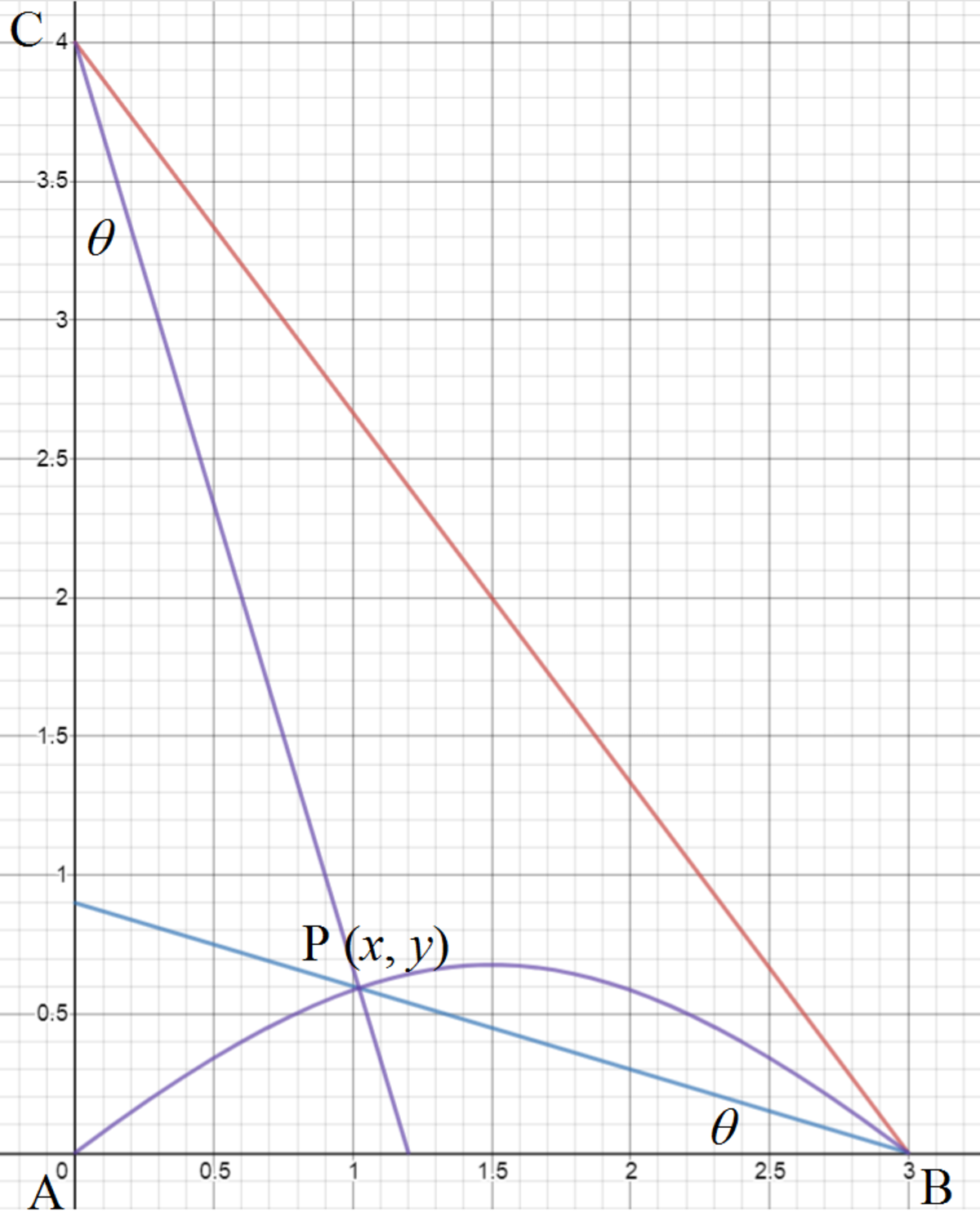
Let A ( 0 , 0 ) , B ( 3 , 0 ) , C ( 0 , 4 ) , P ( x , y ) , and ∠ P B A = ∠ P C A = θ . Then
3 − x y 4 y − y 2 x 2 − y 2 − 3 x + 4 y ( x − 2 3 ) 2 − ( y − 2 ) 2 ⟹ y = tan θ = 4 − y x = 3 x − x 2 = 0 = 4 9 − 4 = − 4 7 = 2 − ( x − 2 3 ) 2 + 4 7
Therefore, the small area is
A = ∫ 0 3 y d x = ∫ 0 3 ⎝ ⎛ 2 − ( x − 2 3 ) 2 + 4 7 ⎠ ⎞ d x = 2 x ∣ ∣ ∣ ∣ 0 3 − ∫ sinh − 1 − 7 3 sinh − 1 7 3 4 7 cosh 2 t d t = 6 − 2 7 ∫ 0 sinh − 1 7 3 cosh 2 t d t = 6 − 4 7 ∫ 0 sinh − 1 7 3 ( cosh 2 t + 1 ) d t = 6 − 4 7 [ 2 sinh 2 t + t ] 0 sinh − 1 7 3 = 6 − 3 − 4 7 sinh − 1 7 3 = 3 − 8 7 ln 7 Let sinh t = 7 2 x − 3 ⟹ cosh t d t = 7 2 d x
Therefore, l + m + n = 3 + 7 + 8 = 1 8 .
@Digvijay Singh , thanks for pointing out my mistake.
The general expression for the two areas is:
A ± = 2 Δ ± 8 ∣ ∣ b 2 − c 2 ∣ ∣ sin A ln ( ∣ b − c ∣ b + c )
where Δ is the area of the triangle.
Log in to reply
Post your solution please. It's a very interesting problem.
Log in to reply
Have a look at my solution. This formula can be obtained by elementary slog, but also by using isogonal conjugacy.
Take A as the origin of coordinates, A C along the x -axis, A B along the y -axis. Then the locus of P is
x 2 − y 2 − 4 x + 3 y = 0
⟹ y = 2 3 + 4 x 2 − 1 6 x + 9
The smaller area is
∫ 0 4 2 3 + 4 x 2 − 1 6 x + 9 d x
= 3 − 8 7 ln 7
So l = 3 , m = 7 , n = 8 and l + m + n = 1 8 .
and hence 2 1 K 2 ( U V − V U ) = ∣ M B A ∣ = 2 1 ∣ A B C ∣ = 2 1 Δ where Δ is the area of the triangle A B C , so that Δ − = 2 1 Δ − K 2 ln ( U V ) Let D be the angle ∠ B M A , and let d = M A be the length of the median from A . Then we have d 2 = 2 1 ( b 2 + c 2 ) − 4 1 a 2 , and hence cos D = a d d 2 + 4 1 a 2 − c 2 = 2 a d b 2 − c 2 so that U V K 4 + U 2 V 2 = M A ⋅ M B = 2 1 a d cos D = 4 1 ( b 2 − c 2 ) while U 2 V 2 ( V − U ) 2 ( K 4 + U 2 V 2 ) = A B 2 = c 2 and hence ( U V − V U ) 2 = U V ( V − U ) 2 = M A ⋅ M B A B 2 = b 2 − c 2 4 c 2 which implies that U V = b − c b + c 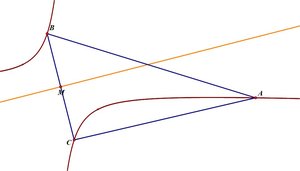 Finally we see that
U
V
−
V
U
=
b
2
−
c
2
4
b
c
and hence
K
2
=
4
b
c
b
2
−
c
2
Δ
=
8
1
(
b
2
−
c
2
)
sin
A
so that the formula for
Δ
−
becomes
Δ
−
=
2
1
Δ
−
8
1
(
b
2
−
c
2
)
sin
A
ln
(
b
−
c
b
+
c
)
What happens when
B
<
C
? In this case the hyperbola is oriented differently, and the portion of the hyperbola that is internal to the triangle is a curve from
A
to
C
, instead of from
A
to
B
(see the final diagram). If
B
=
C
the hyperbola
H
collapses to the perpendicular bisector
L
of
B
C
, dividing the triangle into two triangular regions of equal area
2
1
Δ
.
Finally we see that
U
V
−
V
U
=
b
2
−
c
2
4
b
c
and hence
K
2
=
4
b
c
b
2
−
c
2
Δ
=
8
1
(
b
2
−
c
2
)
sin
A
so that the formula for
Δ
−
becomes
Δ
−
=
2
1
Δ
−
8
1
(
b
2
−
c
2
)
sin
A
ln
(
b
−
c
b
+
c
)
What happens when
B
<
C
? In this case the hyperbola is oriented differently, and the portion of the hyperbola that is internal to the triangle is a curve from
A
to
C
, instead of from
A
to
B
(see the final diagram). If
B
=
C
the hyperbola
H
collapses to the perpendicular bisector
L
of
B
C
, dividing the triangle into two triangular regions of equal area
2
1
Δ
.
To answer the problem, we have a = 5 , b = 4 , c = 3 , A = 9 0 ∘ , so that Δ − = 3 − 8 7 ln 7 , making the answer 3 + 7 + 8 = 1 8 .