Another Rectangular Grid Problem
I drew rectangular grids with one more row than their column. The number of dots in the first four grids are 2, 6, 12, and 20, as shown in the diagram below:
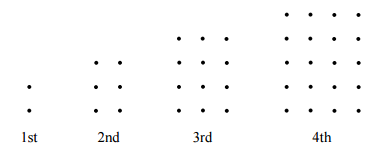
What is the total number of dots used in the first eleven grids?
The answer is 572.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Ah, the good old hockey stick identity .
Log in to reply
Why does it call like that?
Log in to reply
When you circle all of these numbers in pascal's triangle , it looks like a hockey stick due to the single term.
Log in to reply
@Calvin Lin – Haha didn't know that, thanks.
The number of dots in the x t h grid is x ( x + 1 ) = x 2 + x so we are after:
x = 1 ∑ 1 1 x 2 + x
i = 1 ∑ n x = 2 n ( n + 1 ) , i = 1 ∑ n x 2 = 6 n ( n + 1 ) ( 2 n + 1 )
x = 1 ∑ 1 1 x 2 + x = 2 1 1 ( 1 1 + 1 ) + 6 1 1 ( 1 1 + 1 ) ( 2 × 1 1 + 1 ) = 6 6 + 5 0 6
6 6 + 5 0 6 = 5 7 2
Moderator note:
Good usage of these summation formulas.
Did the same way
The matrix of each grid (of n grids suppose) is of the order
n
×
(
n
+
1
)
.
Again, for more proof, the first grid has
2
×
1
=
2
dots
The second grid has
3
×
2
=
6
dots
The third grid has
4
×
3
=
1
2
dots
The fourth grid has
5
×
4
=
2
0
So, the total number of dots upto
n
grids is
n
=
1
∑
1
1
n
(
n
+
1
)
=
5
7
2
I did it in an easy way. I noticed the numbers were increasing by multiples of 2, 2+4=6+6=12+8=20...etc. So I added them all (the 11 terms ) after identifying them.
Certainly, that's easier, though longer.
Relevant wiki: Hockey Stick Identity
In general, the first rectangular grid consists of 1 × 2 dots, the second of 2 × 3 , so the n t h consists of n × ( n + 1 ) points. Thus, the sum we are asked for is 1 × 2 + 2 × 3 + . . . + n × ( n + 1 ) . Note the similarity between each term of the sum and the triangular numbers formula: the k t h term in the previous sum is 2 ( k + 1 2 ) , therefore, the sum can be written as
2 ∑ k = 1 n ( k + 1 2 ) , in which n is the number of columns of the n t h rectangular grid. This sum is equal to 2 times the n t h tetrahedral number: 2 ( n + 2 3 ) = 3 n ( n + 1 ) ( n + 2 )
In the particular case n = 1 1 , 3 1 1 ⋅ 1 2 ⋅ 1 3 = 5 7 2 . Hence, the junction consists of 5 7 2 dots.