Another Series with coefficients in Series

Algebra Level 5

A sequence of number is made like this.

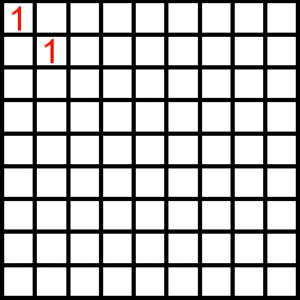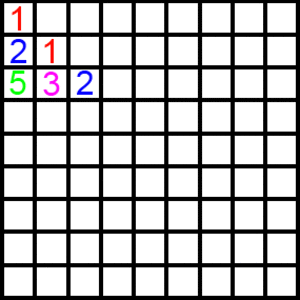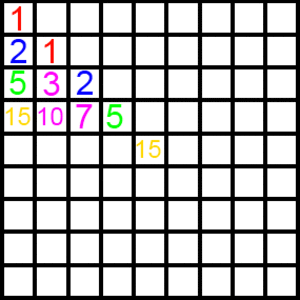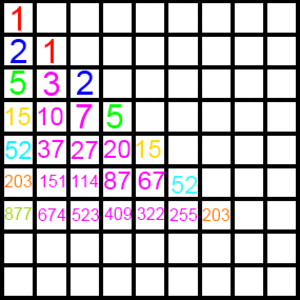
We start with $1$ and we rewrite $1$ in the diagonal column. Then another number is made by filling a box with it's top and right neighbours' sum. And when we arrive at the 1st row, we re-write the result in the next box in the diagonal column,and continue this process.

We then note the numbers of the first rows numbers follow the sequence below

$1,2,5,15,52,203,877,4140, \cdots$

Now a function $f(x)$ is defined as,

$f(x)=x+\frac { 2{ x }^{ 2 } }{ 2! } +\frac { 5{ x }^{ 3 } }{ 3! } +\frac { 15{ x }^{ 4 } }{ 4! } +\frac { 52{ x }^{ 5 } }{ 5! } +\frac { 203{ x }^{ 6 } }{ 6! }+\cdots$

Find $|f(\pi i)|$ .

Notation: $i=\sqrt { -1 }$ denotes the imaginary unit .

The answer is 0.864664716763.

2 solutions

Chew-Seong Cheong
Feb 18, 2019

The sequence of numbers is the Bell numbers $B_n$ , with $B_0 = 1$ missing. The exponential generating function of Bell numbers (see Generating function ) is

$\begin{aligned} B(x) & = \sum_{n=0}^\infty \frac {B_n}{n!}x^n = e^{e^x -1} \\ f(x) & = B(x) - B_0 = e^{e^x-1} - 1 \\ \implies f(\pi i) & = e^{e^{\pi i}-1} - 1 = e^{-2} - 1 \approx -0.865 \end{aligned}$

Therefore, $|f(\pi i)| \approx \boxed{0.865}$ .

Aaghaz Mahajan
Feb 17, 2019

The construction is nothing but the Bell Triangle . And we can also see, that the function defined is the Exponential generating function of Bell numbers without the first term.......And hence, we arrive at the answer easily.....

Thanks for that!, but no kidding,i didn't know that this was something so well known and i thought i just stumbled upon it.

Shauryam Akhoury - 2 years, 3 months ago

No problemmo!! And I know how it feels when something is so well known and you come across it doing some stuff and are elated.....!!! I had this experience when I accidentally stumbled upon Sylvester's Sequence .....But, I have to ask, did you find the exact closed form of the above defined function yourself???

Aaghaz Mahajan - 2 years, 3 months ago

I was solving for x^3/x!'s sum (5e) and i thought what would have been the answer if it were x^4/x! (15e) and then i did this for x^5/x! and then used wolfram after that,i was looking for some pattern in the series 1,2,5,15,52... so i subtracted consecutive terms and then subtracted there difference and arrived at that triangle Then way later (yesterday) i was trying some exponential series questions and thought of e^e^x and found the coefficient's to be similar to this here. I arrived at that function totally by mistake

Shauryam Akhoury - 2 years, 3 months ago

@Shauryam Akhoury – Wow!!! This is great...!!

Aaghaz Mahajan - 2 years, 3 months ago

Another Series with coefficients in Series

The answer is 0.864664716763.

2 solutions

0 pending reports