Anti-Aircraft Marksman

Relevant wiki: Projectile Motion

Assume you fire the cannon with velocities $(x,y,z)$ in the corresponding directions.

We require that $x^2+y^2+z^2=1000^2$

In order for the cannon to hit the aircraft after time t, we also need

$x \times t = 1000 - 400t, \quad y \times t = 2000 + 400t, \quad z \times t - 5t^2 = 3000 + 400t$

solving for $x,y,z$ we get

$x = \frac{1000}{t} - 400, \quad y= \frac{2000}{t} + 400, \quad z= \frac{3000}{t} + 400 + 5t$

Substituting this into $x^2+y^2+z^2=1000^2$ , we get $510000+ \frac{14000000}{t^2}+ \frac{3200000}{t} + 4000t + 25t^2 = 1000^2$ Multiplying through by $t^2$ we get

$510000t^2 +14000000 + 3200000t + 4000t^3 + 25t^4=1000^2 t^2$ $25t^4 + 4000t^3 - 490000t^2 + 3200000t + 14000000=0$

Solving for $t$ we get two positive values

$t=10.2322$ and $t=75.5914$

taking the smaller of the two we get $t=10.2322$

What I thought was interesting about this solution is that it did not require solving for the trajectory of the cannon.

Relevant wiki: Projectile Motion

See the solution by @Daniel Branscombe for a solution based on a polynomial expression for the final time. This is probably the most legitimate way to do it. For fun, I'll post an iterative multi-variate approach as well. We know the launch speed (call it $v$ ). We know the initial position of the aircraft (call it $(P_x,P_y,P_z)$ ) and the aircraft velocity $(v_x,v_y,v_z)$ . We don't know the launch orientation, given by spherical coordinates $\theta$ and $\phi$ . $\theta$ is the angle with respect to the $x$ -axis, and $\phi$ is the angle with respect to the $xy$ plane. We also don't know the intercept time $t_f$ . The equations to solve are:

$P_x + v_x t_f = v\,\cos\theta \, \cos\phi \, t_f \\ P_y + v_y t_f = v\,\sin\theta \, \cos\phi \, t_f \\ P_z + v_z t_f = v\,\sin\phi \, t_f -\frac{1}{2} g t_f^2$

Putting the equations into a different form:

$f_1 = P_x + v_x t_f - v\,\cos\theta \, \cos\phi \, t_f = 0 \\ f_2 = P_y + v_y t_f - v\,\sin\theta \, \cos\phi \, t_f = 0 \\ f_3 = P_z + v_z t_f - v\,\sin\phi \, t_f +\frac{1}{2} g t_f^2 = 0$

Then we form a Jacobian matrix consisting of partial derivatives of the three functions with respect to the unknowns $(\theta, \phi, t_f)$ . Then we iterate as indicated in the scan. Note that only one element in the matrix equation has a "k" subscript, indicating "present iteration", instead of "k-1" for "previous iteration". This is what is being solved for.

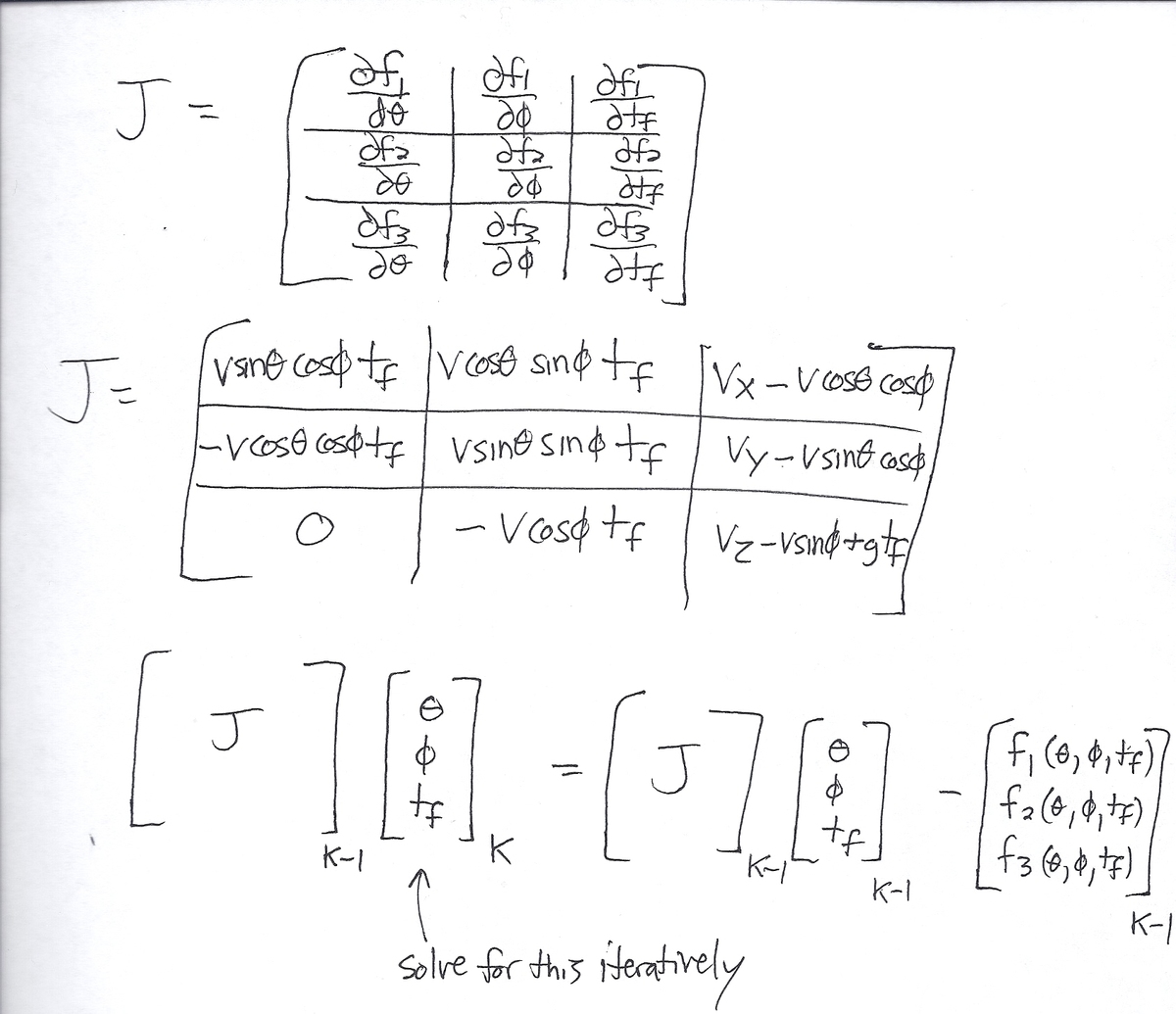
Solutions (sometimes it converges to one solution, and sometimes it converges to the other, depending on random initial conditions):

theta
2.04052416931
phi
0.839563864441
tf
10.2322479847


theta
2.30743135526
phi
0.957306849804
tf
75.5913931928