Ants are smart
Suppose there is a smart ant meaning it can teleport. And it is placed in one of the corners cell of a 3 × 3 grid. Now if the probability that the ant lands in the centre cell in 4 moves is α . Then enter ⌊ 1 0 ⁶ α ⌋ as the answer.
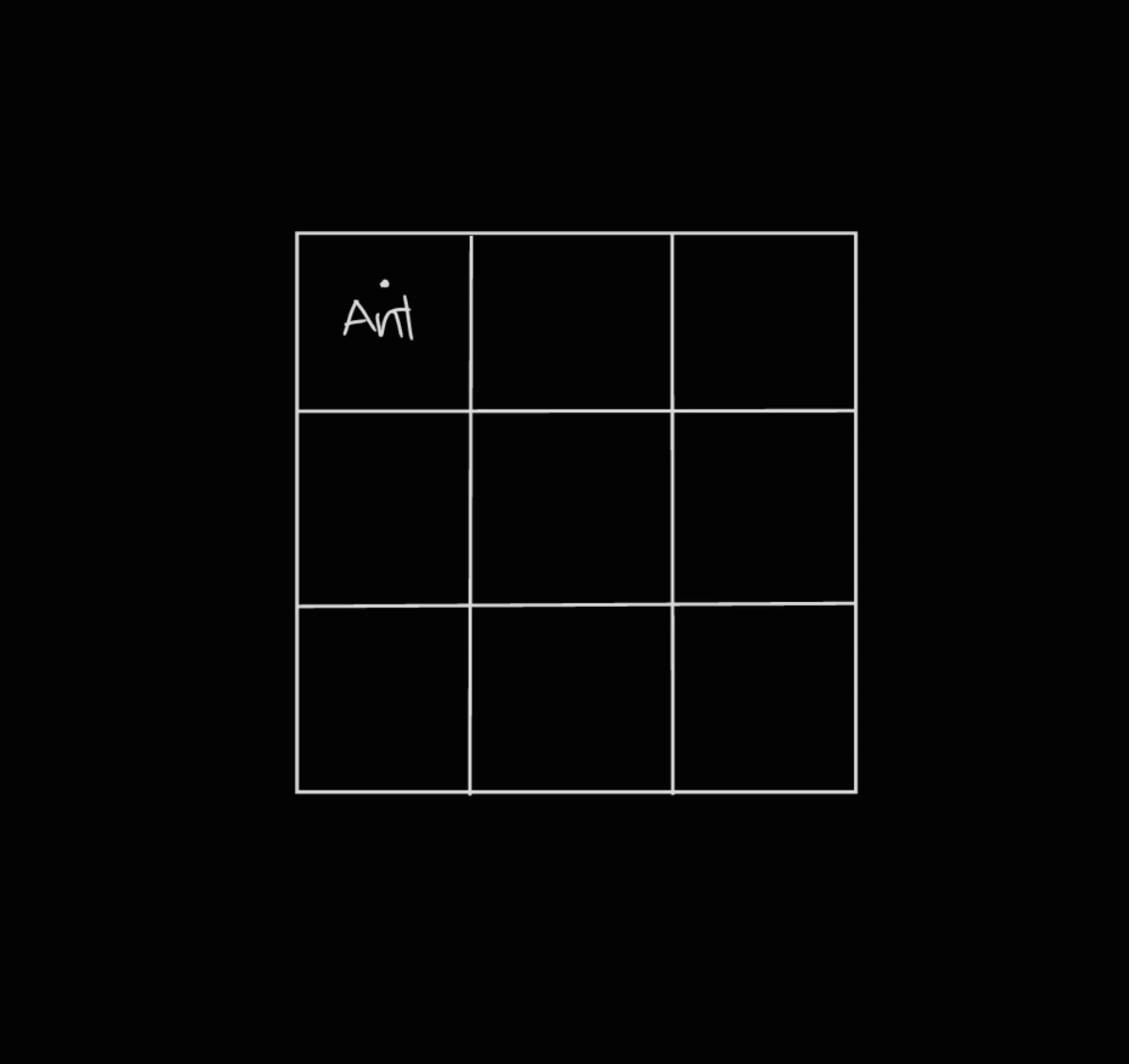 This represents the initial position of Ant.
This represents the initial position of Ant.
Note:
- The ant can teleport only if it's in a cell and there no adjacent cell on top or right or left of it , so now if it goes up it will back down in bottom row. See the image for better understanding.
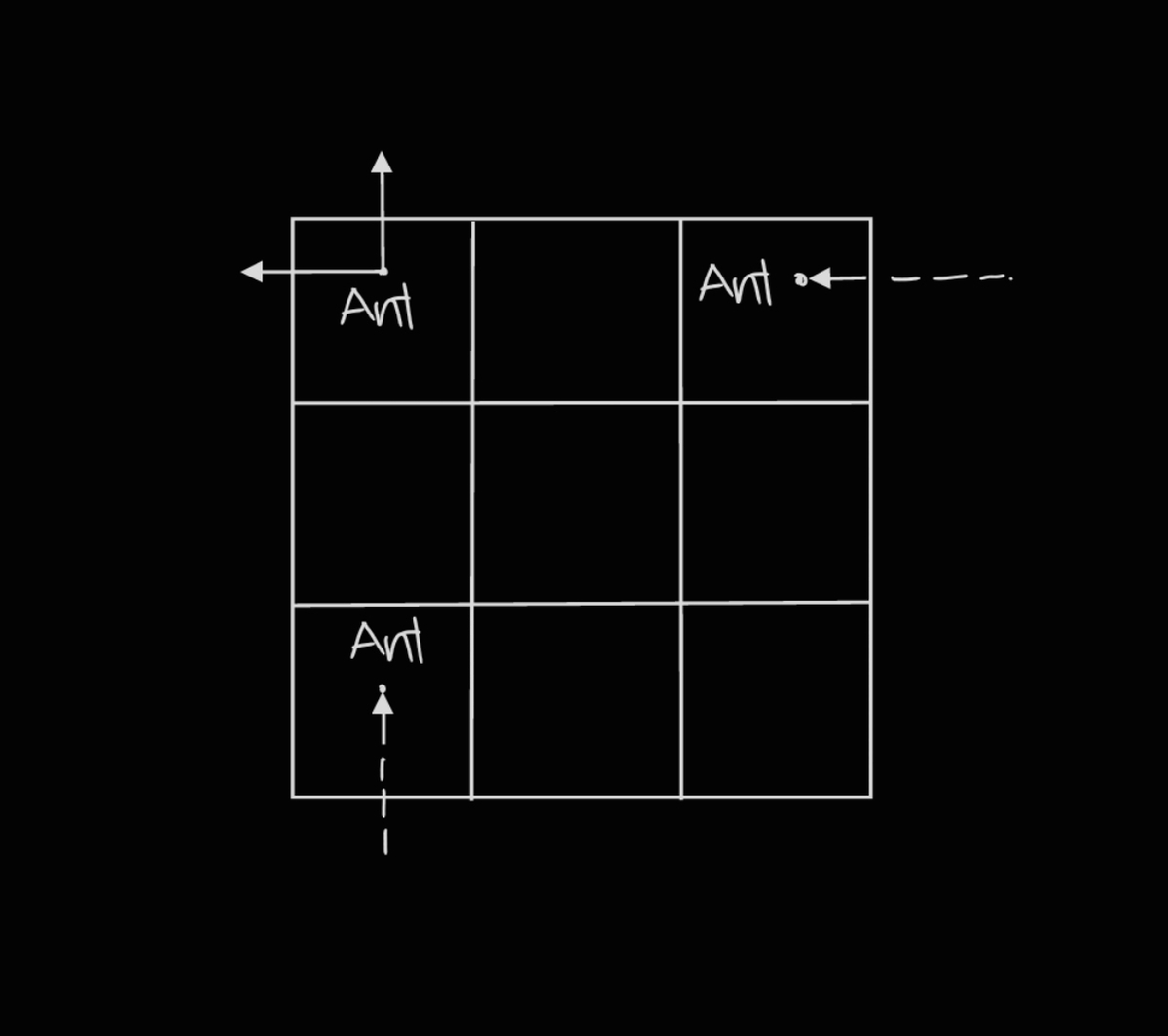 In the above image you can see that if ants moves up it warps to the bottom row, similarly if ant moves left it warps to rightmost column.
In the above image you can see that if ants moves up it warps to the bottom row, similarly if ant moves left it warps to rightmost column.
- 1 move = moving from 1 cell to another cell (diagonal moves aren't allowed).
The answer is 117187.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This problem can be solved using Markov chains. If we label the grid as follows:
| A | B | C |
| D | E | F |
| G | H | I |
then the transition matrix M (which shows the probability of moving from the cell in the left column to the cell in the top row) is
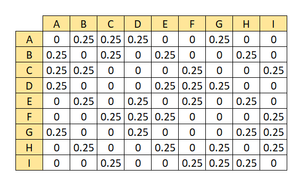
(the ant has probability 4 1 ) of move to any of its four orthogonally adjacent cells)
To find the probabilities for where the ant might be after four moves, we just calculate M 4 and read off the top row. Putting this back into the original grid, we get
| 2 5 6 3 6 | 2 5 6 2 5 | 2 5 6 2 5 |
| 2 5 6 2 5 | 2 5 6 3 0 | 2 5 6 3 0 |
| 2 5 6 2 5 | 2 5 6 3 0 | 2 5 6 3 0 |
so the answer we want is ⌊ 1 0 6 ⋅ 2 5 6 3 0 ⌋ = 1 1 7 1 8 7 .
NB: The different states (and therefore the transition matrix) could be simplified by noting the symmetry along the main diagonal of the grid. This makes the matrix smaller, but the transitions are a little less obvious.
 Refer to the above image
Refer to the above image
We can see that by symmetry all the corner cells are equivalent, and the cells except the corner and center are also equivalent by symmetry.
Now let us mark the probability of the ant coming from (in n moves towards the center)
- center to center = c n
- corner to center = a n
- others to center = b n
Now,
- from one corner, the ant has 4 ways to move to ther cells, that is 2 ways to other corners or 2 ways to cells marked as b.
- from one cell marked as b, the ant has 4 ways to move to ther cells, that is 2 ways to corners or 1 way to other cell marked as b or 1 way to the center cell.
- from the center, the ant has 4 ways to move to ther cells, that is 4 ways to cells marked as b.
Now if ant is supposed to finish in n moves from a cell, and now suppose it makes a move to the next cell, then from that cell it has move to the center in n - 1 moves.
Now by using Recurrence Relations we get,
- a n = 0.5 a n − 1 + 0.5 b n − 1
- b n = 0.5 a n − 1 + 0.25 b n − 1 + 0.25 c n − 1
- c n = b n − 1
Now solve the equations with a 0 = b 0 = 0 and c 0 = 1. We get a 4 = 0.1171875. Therefore answer is 117187.
Nice approach! Just one thing - the corners aren't all symmetric. You can check this numerically with a bit of code or have a look at my solution. Alternatively, you can get symmetry by shifting the grid; if the original grid you drew is
| A | B | C |
| D | E | F |
| G | H | I |
then sliding it one place right and one place down gives
| I | G | H |
| C | A | B |
| F | D | E |
So the symmetries are E = F = H = I and B = C = D = G .
Also, fun fact: the way you've joined the edges up makes the grid a map of a torus!
Log in to reply
By symmetry, I didn't mean exact symmetry I meant like the probability of it coming from the corner is same for all corners. Yea I was not able draw a 3D image, that is why I drew a 2D image with warping ability.
Log in to reply
ah, sorry, I misinterpreted your solution. Nice problem, by the way!
