Ants on a cylinder
Brilli the ant is late. He was supposed to meet his Aunt Milly on the other side of the fencepost ten minutes ago, but got chatting about maths puzzles with his friend Billy. (In particular, this inspirational one .)
The fencepost they're all on is shaped, conveniently, like a cylinder, with radius 5 c m . Brilli is at a point B , 2 c m below the (perfectly flat and circular) top of the post. Aunt Milly is waiting for him at point M , 1 c m below the top. The angle separating their positions (as viewed from directly above the fencepost) is 1 5 0 ∘ :
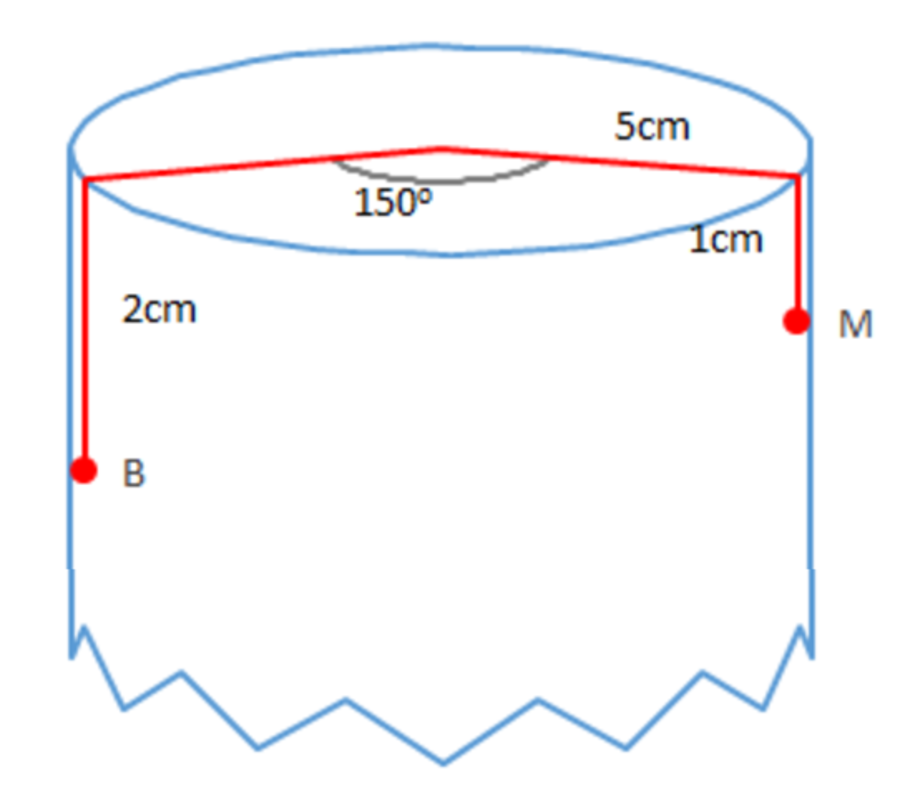
To get to his Aunt, Brilli has to walk on the surface of the cylinder − no shortcuts through the middle (he's not a termite, after all).
Billy thinks the shortest route takes more than 1 3 c m . Brilli thinks Billy is a silly ant, and that he can do better. Who's right?
If the length (in c m ) of the shortest possible path along the surface of the fencepost Brilli can take to reach his aunt is p , submit ⌊ 1 0 0 p ⌋ as your answer, where ⌊ ⋅ ⌋ is the floor function . (Ants appreciate this level of precision.)
The answer is 1251.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Very nice, thanks for sharing your solution. I wonder, is there a way to solve this similar to your solution of the inspiration problem? (If you recall, you unfolded a net in that question, then solved geometrically.)
Log in to reply
I think so. It just the inspiration problem, I can get away with changing 3-D to 2-D.
Let's find the optimal path. If we won't come on top of the cylinder the path would take ( 5 ∗ 6 5 π ) 2 + ( 2 − 1 ) 2 > 1 3 . So, let's call the entry point C and the exit point N , thus we have two right triangles △ A B C and △ L M N , where A and L - points on the top directly above B and M accordingly (they become right triangles when we place the side of the cylinder on a plane). O is the center of the top side of the cylinder, △ C O N is an isosceles triangle with legs O C = O N = 5 . Our path then is the polygonal chain ( B , C , N , M ) .
Let's deconstruct the cylinder into a rectangle (the sides) and a circle (the top) and place them on a plane, so that the circle touches rectangle in point N . Then points C , N , M should be inline, otherwise the path isn't minimal: we can draw a segment C M which would be shorter and moreover the part that isn't in the circle or rectangle is "non-existent", so new path is even shorter. O N ⊥ L N and L M ⊥ L N , so O N ∥ L M . And since C N M is one line, ∠ C N O = ∠ N M L .
Similarly, we can prove that ∠ N C O = ∠ C B A . △ C O N is an isosceles triangle which means ∠ C B A = ∠ N C O = ∠ C N O = ∠ N M L = α . Since △ A B C and △ L M N are right triangle, they are similar with coefficient 2 and L N = cos α 1 and A B = cos α 2 . △ C O N is an isosceles triangle with legs O C = O N = 5 , so C N = 1 0 cos α . Thus the path length is cos α 3 + 1 0 cos α , we just need to find α .
That's the tricky part where I kinda cheated, so beware. Let's focus on arcs of the top circle. We know the lengths of arcs ∩ N L = tan α and ∩ A C = 2 tan α because we know other sides of the right triangles. Arc ∩ C N has length 5 ∗ ∠ C O N = 5 ∗ ( π − 2 α ) = 5 π − 1 0 α . But ∠ A O L = 6 5 π , so ∩ A L = 6 2 5 π . So we have:
∩ A C + ∩ C N + ∩ N L = ∩ A L
3 tan α + 5 π − 1 0 α = 6 2 5 π
α = 1 2 π + 1 0 3 tan α
And this is the moment where I cheated: I typed the equation in WolframAlpha and got the root, α = 0 . 3 8 2 4 9 0 3 6 4 7 6 4 6 6 7 . . . The equation doesn't seem to have an analytical answer but it would be nice if someone proved me wrong.
Now we can calculate the minimal path length, cos α 3 + 1 0 cos α = 1 2 . 5 1 1 0 5 1 7 6 7 6 5 3 9 9 0 1 7 0 . . . The answer is 1 2 5 1 .
Great solution! Different to my approach, too.
One note - you mention you felt numerical methods were "cheating" in your solution, but however you solve it, you have to use numerical methods (or Wolfram|Alpha) at some point - because you get a transcendental equation (in yours, you have a mix of terms in α and in tan α ). So definitely not cheating!
I'd be interested to see a diagram showing your deconstructed cylinder net - I think that's the key to getting a "nice" solution here (my solution wasn't very nice, I'm afraid).
@Nick Kent
,
@Chris Lewis
-
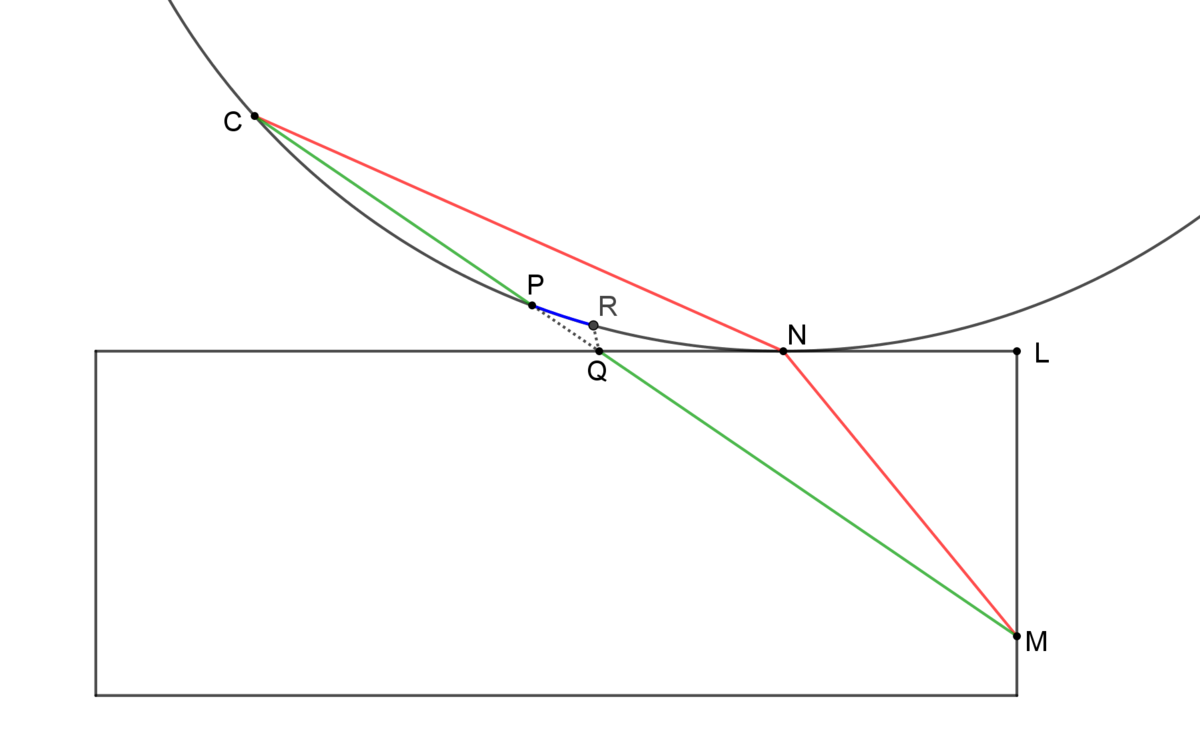 “… points C, N, M should be inline, otherwise the path isn't minimal: we can draw a segment CM which would be shorter and moreover the part that isn't in the circle or rectangle is "non-existent", so new path is even shorter.”
“… points C, N, M should be inline, otherwise the path isn't minimal: we can draw a segment CM which would be shorter and moreover the part that isn't in the circle or rectangle is "non-existent", so new path is even shorter.”
Although the statement that points C , N , M should be collinear is true, I don’t think the explanation that follows is correct. If we reconstruct the cylinder, the points of intersection of the segment C M with the circle and the rectangle (points P and Q in the figure) don’t coincide and hence the two green segments are not the complete path. They are just a part of the path to which we have to add the arc P R , where R is the point of the circle that coincides with point Q . It is true that the length of the arc P R is smaller than the length of segment P Q , but this is something we need to prove.
Log in to reply
Thanks, Thanos - I've posted a solution now which uses a similar idea (I was determined to find a straight line somewhere). Mine is a bit of an unwieldy explanation but hopefully it makes sense!
First step: look for the optimal distance on the side of the fencepost. "Unrolling" the cylinder we have a right triangle with sides 1 and the arc formed by the 150° angle.
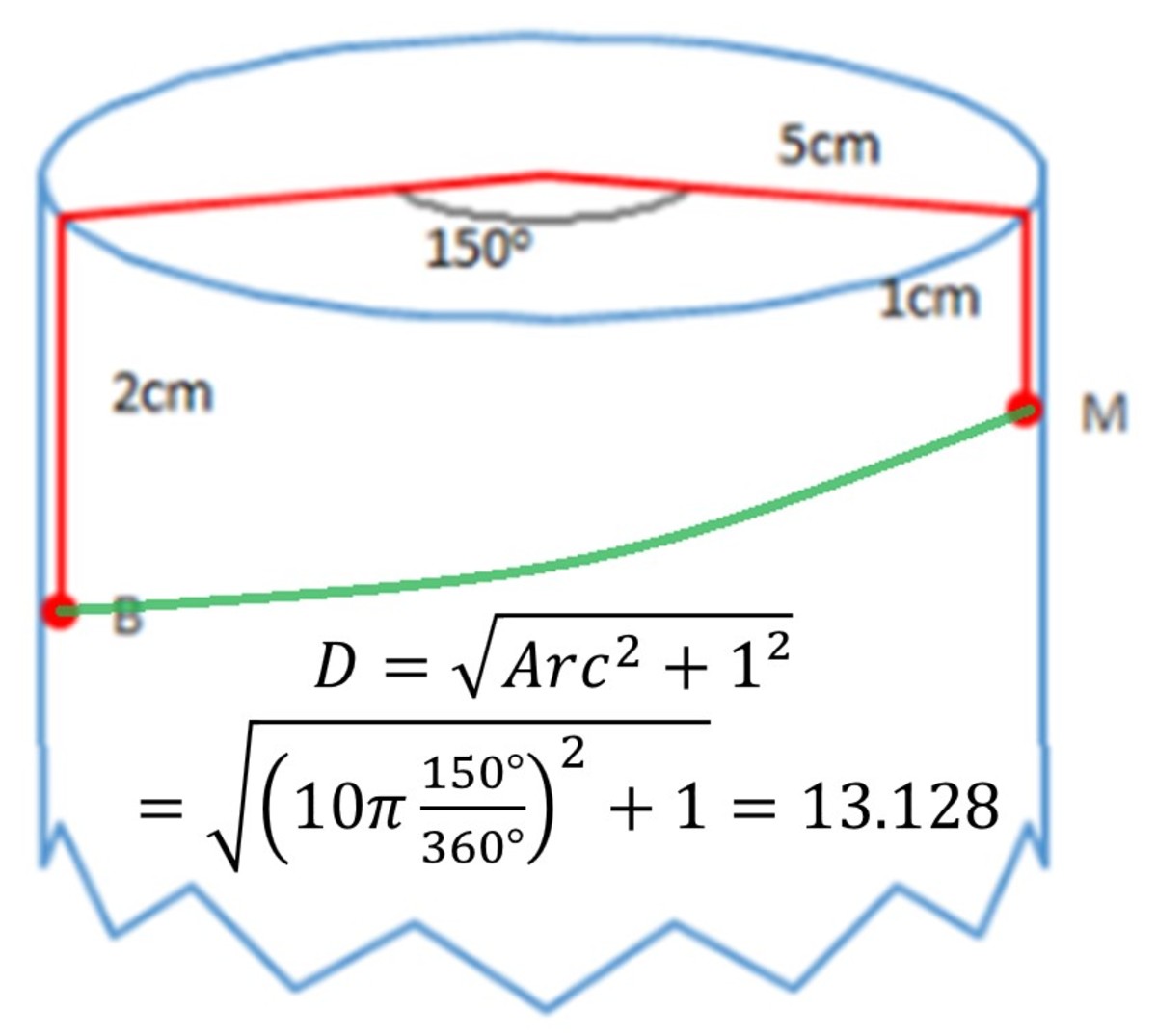
Nope! Longer than the full red distance passing by the center of the fencepost. It's shorter if we take the chord of the 150° angle, but we can do better, let's look how we can find the best angle to optimise his walk on the fencepost.

We know that the shortest path is a straight line. With the same angle in the center, the angle on the outside of the post change by a factor of two since Milly is twice the distance from the top than Brilli. The optimal straight line thus have angles that are x and x/2.
This is the equation representing the distance that Brilli will walk, depending on the angle x from the center, and its graphic (from Pythagor and the calculation of a chord).
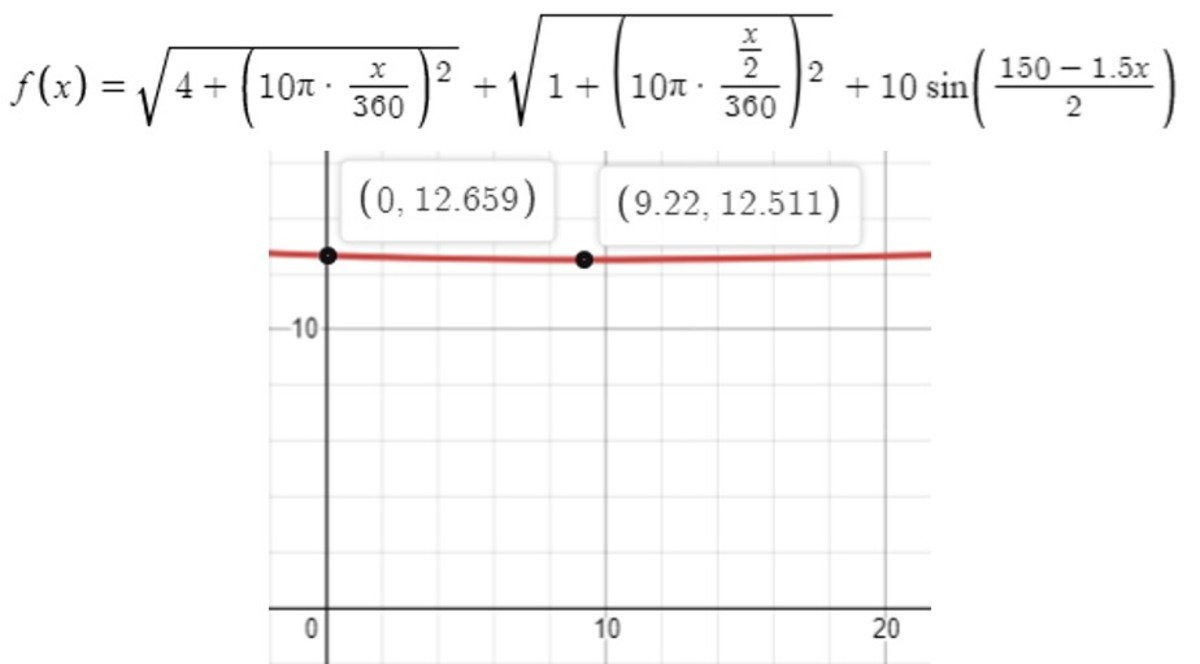
With the floor function as 100p, we thus have 1251! But anyway Brilli and Milly should be social distancing by now lol!
The key idea here is to find a way to "unfold" the cylinder into a flat net. Then the shortest path will be a straight line on that net. This gets a bit involved, so I've split the solution into a few parts.
Brilli has two options; stay on the curved surface, or cross over the flat top of the fencepost. It's difficult to find a single way to address these, so I'll do them separately. But first...
Part 0: preliminaries
Let's start with notation. I want to solve the general problem, so let the radius of the fencepost be r ; let Brilli's distance from the top be a ; let Milly's be b ; and let the angle separating them be α . So in this case r = 5 , a = 2 , b = 1 , and α = 1 5 0 ∘ = 6 5 π rad (I'll be using radians for the rest of this solution).
For convenience, let's also define a cylindrical polar coordinate system ( ρ , θ , z ) : say the z -axis is the axis of the cylinder, with the origin at the centre of the top of the of the fencepost, and take the positive z direction to be downwards. Also, say Brilli starts at θ = 0 . The coordinates of the start and end points are then B ( r , 0 , a ) and M ( r , α , b ) .
Part 1: what if we stay on the curved surface?
Brilli has to travel a distance of r α in the θ direction, and ∣ b − a ∣ in the z direction. Since these are perpendicular, the straight-line distance (on the "unwrapped" curved surface) is, by Pythagoras, D curved = r 2 α 2 + ( b − a ) 2
In this problem, this is about 1 3 . 1 2 8 cm (this was Billy's suggestion, by the way).
Part 2: crossing the top
Alternatively, Brilli can try going over the top of the fencepost. This path will take Brilli from his starting point B to a point B ′ where he moves from the curved surface to the flat top of the post, across the top to a point M ′ , and down to Milly at M .
To find our optimal straight line path, we need to unwrap the cylinder into its net. This net consists of a circle (the top of the fencepost) and a rectangle corresponding to the curved surface. The trick is to cut this rectangle into two smaller rectangles, one of which is tangent to the circle at B ′ and the other at M ′ :
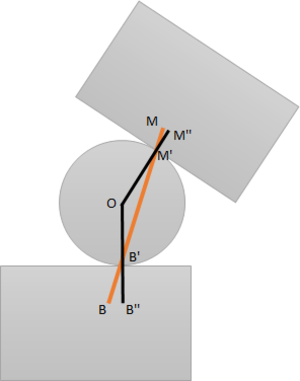
The orange line represents the optimal path (which is a straight line on the net).
Point B ′ ′ has the same z coordinate as B and the same θ coordinate as B ′ , so that Δ B B ′ B ′ ′ has a right-angle at point B ′ ′ . Point M ′ ′ is defined likewise.
Let the angle ∠ B ′ O M ′ = 2 ϕ . Then ∠ B ′ B ′ ′ B = ∠ M ′ M ′ ′ M = ϕ .
We can (finally) work out some distances. Considering triangle Δ B B ′ B ′ ′ , we have B ′ B ′ ′ = a , B B ′ ′ = a cot ϕ , B B ′ = sin ϕ a
Similarly, M ′ M ′ ′ = b , M M ′ ′ = b cot ϕ , M M ′ = sin ϕ b
Crossing the circle, we have B ′ M ′ = 2 r sin ϕ . So the length of the path is D top = B B ′ + B ′ M ′ + M ′ M = sin ϕ a + b + 2 r sin ϕ
Now, recall that the θ -component of the distance between B and M is r α . But we can also work this out on the net diagram; we have r α = B B ′ ′ + 2 r ϕ + M M ′ ′ = ( a + b ) cot ϕ + 2 r ϕ
This gives us an equation we can solve (numerically) in ϕ ; in this case, we get ϕ ≈ 1 . 1 8 8 , which gives D top = 1 2 . 5 1 1 0 5 …
Since this is the shorter of the two distances, it is optimal, giving the problem's answer 1 2 5 1 .
Part 3: solving for ϕ
To find ϕ , we had to solve the equation ( a + b ) cot ϕ + 2 r ϕ = r α
This is a transcendental equation, so has to be solved numerically. It's easy to plug into Wolfram|Alpha, or use Newton-Raphson; but a nice alternative is to simply iterate ϕ n + 1 = 2 r r α − ( a + b ) cot ϕ n
for some sensible starting value of ϕ 0 (eg 4 π ).
We in fact get more than one solution for ϕ , but it's easy to check among these for optimality. A nice property of the above iteration scheme is that only the optimal solution is stable (ie, for just about any starting value, it will converge to the correct ϕ ).
Hi Chris! This is a very nice clear and inventive solution. Just one concern: I still don't see why, in the optimal path, points B , B ′ , M ′ and M have to be collinear. I have the feeling something is missing there... Can you give an explanation for the statement? Perhaps a diagram showing the differense.
Log in to reply
Thanks! My reasoning was that optimal paths will always be straight lines in some unfolding of the net (as then we simply have the shortest distance between two points in a plane).
Having said that, though, I can see what you're getting at; why can't there be a different unfolding that uses a sort of zig-zag line that winds up shorter?
I'm definitely missing something - I'll see if I can come up with a formal justification. It would be nice to do this a non-calculus way, but I'm struggling to think of one.
(By the way, I hope I understood your comment correctly - if instead you meant you have found a shorter path please let me know!!)
Log in to reply
 "why can't there be a different unfolding that uses a sort of zig-zag line that winds up shorter?"
"why can't there be a different unfolding that uses a sort of zig-zag line that winds up shorter?"
That is excactly my point. How can we be sure that there is not another path like the one shown in my figure.
I agree that it will be very nice if we find a non-calculus solution. Still trying...
Log in to reply
@Thanos Petropoulos – Thanks for the diagram. We'll need some new notation; let's keep ∠ B ′ O M ′ = 2 ϕ (I'm fairly sure the " 2 " helps keep things neat), and define ∠ B ′ B B ′ ′ = β , ∠ M ′ M M ′ ′ = μ .
We still have B ′ B ′ ′ = a , M ′ M ′ ′ = b
so the distance travelled is D = B B ′ + B ′ M ′ + M ′ M = sin β a + 2 r sin ϕ + sin μ b
and we also have the constraint that r α = B B ′ ′ + 2 r ϕ + M M ′ ′ = a cot β + 2 r ϕ + b cot μ
This is where I run out of inequality knowledge and feel tempted to resort to Lagrangian multipliers.
Log in to reply
@Chris Lewis – As I'm out of other ideas: put F ( ϕ , β , μ , L ) = sin β a + 2 r sin ϕ + sin μ b + L ( a cot β + 2 r ϕ + b cot μ − r α )
Differentiating: F ϕ F β F μ F L = 2 r ( L + cos ϕ ) = − a csc β ( cot β + L csc β ) = − b csc μ ( cot μ + L csc μ ) = a cot β + 2 r ϕ + b cot μ − r α
Setting all these to zero, we get cos ϕ + L = cos β + L = cos μ + L = 0
So, hooray, but given how quickly this appears I still feel there's a non-calculus way that's eluding me. Do you know of any geometric interpretation of Lagrangian multipliers that could work here?
Log in to reply
@Chris Lewis
–
This is a nice proof of the collinearity of
B
,
B
′
,
M
′
,
M
. But still... it is calculus. Sadly, for the moment I don't have any geometric interpretation of Lagrangian multipliers.
In my solution I also used calculus: a function of two variables, similar to the one Chew-Seong Cheong gave in his solution, then I located the critical numbers and performed the second partials test. But this is not a geometric approach.
Actually if Billi were to walk up from B to A , then to E and down to M , it would only be 2 + 2 × 5 sin 7 5 ∘ + 1 ≈ 1 2 . 6 6 < 1 3 . So Billy isn't that smart. This also tells Billi that it is worthwhile to climb up.
Let ∠ A O C = α and ∠ D O E = β . Then the length of the path B - C - D - M is given by:
ℓ = B C + C D + D M = 2 2 + ( 5 α ) 2 + 2 × 5 sin ( 2 6 5 π − α − β ) + 1 2 + ( 5 β ) 2 = 4 + 2 5 α 2 + 1 0 sin ( 1 2 5 π − 2 α − 2 β ) + 1 + 2 5 β 2
Let us check, if we fix the value of β , what value of α minimizes ℓ . We apply
∂ α ∂ ℓ ⟹ 4 + 2 5 α 2 2 5 α = 4 + 2 5 α 2 2 5 α − 5 cos ( 1 2 5 π − 2 α − 2 β ) = 5 cos ( 1 2 5 π − 2 α − 2 β ) Putting ∂ α ∂ ℓ = 0
This means that for any value of β , α minimizes ℓ , when 4 + 2 5 α 2 5 α = cos ( 1 2 5 π − 2 α − 2 β ) . Similarly, we find that for any value of α , β minimizes ℓ , when 1 + 2 5 β 2 5 β = cos ( 1 2 5 π − 2 α − 2 β ) . Therefore ℓ is minimized, when
4 + 2 5 α 2 5 α 4 + 2 5 α 2 α 2 ⟹ α ⟹ 1 + 2 5 β 2 5 β ⟹ sin ( 1 2 5 π − 2 3 β ) = 1 + 2 5 β 2 5 β = cos ( 1 2 5 π − 2 α − 2 β ) = 1 + 2 5 β 2 β 2 = 2 β = cos ( 1 2 5 π − 2 3 β ) = 1 + 2 5 β 2 1
Solving numerically, we have β ≈ 0 . 0 8 0 4 6 0 6 5 1 . Substitute in ℓ min = 3 1 + 2 5 β 2 + 1 + 2 5 β 2 1 0 ≈ 1 2 . 5 1 1 0 5 1 7 7 . Therefore ⌊ 1 0 0 p ⌋ = 1 2 5 1 .