Apollonius' Riddle
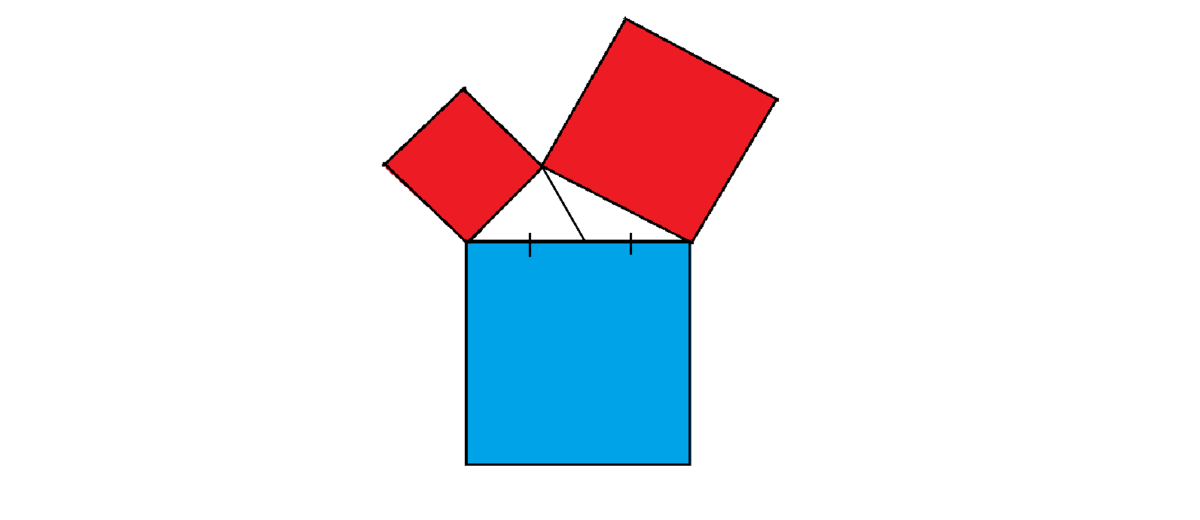
Apollonius, the famous mathematician, was invited by the King of Perga for a geometry session. Apollonius first presented the painting of the 3 squares rearranged to form a triangle with a median splitting the largest side, as shown above.
Apollonius : O my great King, behold this beautiful diagram! The Lord of the North has 2 pieces of red square lands while the Lord of the South has 1 larger blue square land. Their sides including the median all have lengths in whole integers.
King : Beautiful indeed, my teacher!
Apollonius : Then does thy greatness know who has more land?
King : I've heard that the Lord of the South has more (blue) land by 26.
Apollonius : Now then all side lengths are known. Please tell me, my wise one. What is the perimeter of this triangle?
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Why have you typed 1 5 0 up there; shouldnt it be 2 6 ?
Now, consider these triplets for
(
a
,
b
,
c
)
(
3
,
1
7
,
1
8
)
;
(
5
,
2
5
,
2
6
)
;
(
7
,
3
7
,
3
8
)
;
(
9
,
5
3
,
5
4
)
;
(
1
1
,
7
3
,
7
4
)
and so on; why are all these invalid?
Now, listen I think where you (or me) have messed up is;
the lengths of the median and
m
need not be whole numbers; which you have assumed to get to the answer
Log in to reply
In the question, Apollonius said it had to be integer.
Log in to reply
But; he had said about the sides of the square (and consequently the triangle); and not the median of the triangle.
Log in to reply
@Yatin Khanna – Sorry. Just edited.
Log in to reply
@Worranat Pakornrat – Seems fine now.
L e t a , b , c b e t h e s i d e s , c > a , b , a n d d t h e m e d i a n a l l i n t e g e r s . ∴ a 2 + b 2 = c 2 − 2 6 . . . . . . . ( ∗ ∗ ) B u t d 2 = 2 1 ∗ ( a 2 + b 2 ) − 4 1 ∗ c 2 = 2 1 ∗ ( c 2 − 2 6 ) − 4 1 ∗ c 2 = 4 1 ∗ c 2 − 1 3 . ⟹ 4 1 ∗ c 2 − d 2 = 1 3 . ⟹ ( 2 1 c − d ) ( 2 1 c + d ) = 1 3 . S i n c e c , a n d d a r e i n t e g e r s , o n l y s o l u t i o n i s ( 2 1 c − d ) = 1 , a n d ( 2 1 c + d ) = 1 3 . ∴ c = 1 4 . S o f r o m ( ∗ ∗ ) , a 2 + b 2 = 1 9 6 − 2 6 = 1 7 0 . S i n c e t h i s i s e v e n , b o t h a a n d b a r e e v e n o r o d d . H o w e v e r t h e s u m o f t w o s q a u r e s h a s z e r o i n u n i t d i g i t . S i n c e 2 1 7 0 = 8 5 N O T a s q u a r e . W L O G a < b . ∴ ( A ) { 5 ∣ a a n d 5 ∣ b } , o r ( B ) { ( 4 o r 6 ) ∣ a a n d ( 6 o r 4 ) ∣ b } , o r ( C ) { ( 1 o r 9 ) ∣ a a n d ( 9 o r 1 ) ∣ b } ( A ) 1 7 0 − 5 2 = 1 4 5 N O T a s q u a r e . N o o t h e r c o m b i n a t i o n h e r e c a n g i v e a t o t a l o f 1 7 0 . ( B ) 1 7 0 − 4 2 = 1 5 4 , N O T a s q u a r e , 1 7 0 − 6 2 = 1 3 4 N O T a s q u a r e . N o o t h e r c o m b i n a t i o n h e r e c a n g i v e a t o t a l o f 1 7 0 . ( C ) 1 7 0 − 1 2 = 1 6 9 = 1 3 2 . s a t i s f y ( ∗ ∗ ) , B u t 1 , 1 3 , 1 4 i s a s t . l i n e . 1 7 0 − 3 2 = 1 6 1 N O T a s q u a r e . . . . . 1 7 0 − 7 2 = 1 2 1 = 1 1 2 . s a t i s f y ( ∗ ∗ ) , S o a = 7 a n d b = 1 1 . A n s w e r . 1 4 + 1 1 + 7 = 3 2 .
You can't draw a triangle with sides 1, 13, 14: it will be a straight line.
Nice casework here.
More generally, we can use gaussian integers to help solve a 2 + b 2 = n .
Log in to reply
Thank you for pointing out, a new for me.
According to Apollonius' theorem, for a triangle, with side lengths a , b , c , where c = 2 m , and the median length d as shown, a 2 + b 2 = 2 ( d 2 + m 2 ) .
This can be rewritten as a 2 + b 2 − c 2 = 2 ( d 2 − m 2 ) = 2 ( d − m ) ( d + m ) .
Or c 2 − a 2 − b 2 = 2 ( m − d ) ( m + d ) .
In the question, the blue land has larger area than the red ones by 2 6 .
Hence, c 2 − a 2 − b 2 = 2 6 = 2 ( m − d ) ( m + d ) .
1 3 = ( m − d ) ( m + d ) .
Since all side lengths are all in integers, there are only one possibility: 1 3 = 1 ⋅ 1 3 .
Then if we add the factors together, ( m − d ) + ( m + d ) = 2 m = c = 1 + 1 3 = 1 4 .
Then m = 7 and d = 6 .
Thus, a 2 + b 2 = 2 ( d 2 + m 2 ) = 2 ( 6 2 + 7 2 ) = 1 7 0 .
Then there are two possibilities: 1 7 0 = 1 2 + 1 3 2 = 7 2 + 1 1 2 .
However, if a = 1 ; b = 1 3 ; c = 1 4 , only a straight line can be drawn.
Therefore, a = 7 ; b = 1 1 ; c = 1 4 , and the perimeter is 7 + 1 1 + 1 4 = 3 2 .