Approximate Pythagoras

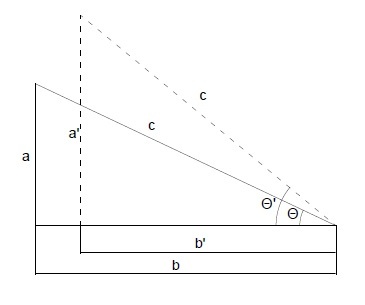
Let $a=1$ then the approximation, which is always an overestimate, can be written as $b+0.5 \approx \sqrt{1+b^{2}}$

We then need to maximize $f(b)=\frac{b+0.5}{\sqrt{1+b^{2}}}$

Which has derivative $f'(b)= \frac{1}{\sqrt{1+b^{2}}}-\frac{b(b+0.5)}{(1+b)^{3/2}}$

Solving $f'(b)=0$ gives $b=2$ and $f(2)=\frac{\sqrt{5}}{2}$

So $a=1$ , $b=2$ , $p=5$ , $q=2$ and $a+b+p+q=\boxed{10}$

---

If this problem is of interest to you, the harder follow-up is A better approximate Pythagoras

From the fig., keeping C constant, as θ is varied, b and a vary,

Difference, δ = (b + a/2) - c

or, δ = ccosθ + 0.5csinθ – c

Differentiating with respect to θ we get,

cotθ = 2, or b/a = 2

∴(b+a/2)/c =√5/2

∴ a + b + p + q = 10