This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I'd like to know who keeps editing the problem and for what reason. I outlined my reasons above of why I want to keep the exact phrasing.
Log in to reply
We were wanting to use your problem for Problems of the Week.
Given your strong feelings about the phrasing, I have reverted the changes to your problem. I will feature the S ( n 4 ) problem instead.
Log in to reply
Yeah, it's intended to be a quirky problem and I didn't expect it to be featured. Popular, maybe, but definitely not what I thought would go to Problems of the Week. Of course, I can make another version (with a different circuit) that does actually say what you're supposed to do, and you can put that one in, if you want.
Log in to reply
@Ivan Koswara – If you can make another version, that would be great! I can use it for the following week :)
I like the "self-referential" logical deductions that have to be made with this problem, and I do think it will appeal to the advanced group.
Sorry for the confusion.
Log in to reply
@Calvin Lin – Was a circuit problem like this featured at any time? If not, it would be interesting to see some. Thx.
Log in to reply
@Wesley Zumino – I don't think this or the other version was featured.
Log in to reply
@Ivan Koswara – Yea, it wasn't featured during that week/time period. It did make it into the consideration process, but we ended up going with other problems.
Personally, I find logic circuits and (separately) self-referential questions interesting :)
Log in to reply
@Calvin Lin – @Calvin Lin Perhaps the GF(2) approach might provide some insight for constructing interesting systems of equations to solve. I can give it some thought, perhaps drawing some inspiration from this and @Ivan Koswara 's other circuit problem and that circuit at the codeforces link. It would be a fun exercise. Unfortunately right now I am coming into a busy period...need another burner on my increasingly expanding stove...
Log in to reply
@Wesley Zumino – LOL I hear you! I just need each day to be 48 hours long.
I would be excited to see what you come up with.
BTW, @Ivan Koswara , cute problem. Thank you for sharing it.
I took an (abstract) algebraic approach with the
finite (Galois) field
G
F
(
2
)
(just
{
0
,
1
,
+
,
⋅
}
with mod 2 arithmetic). I haven’t seen this here yet, so I thought I’d share it. First, express the logical gate operators as algebraic expressions in operators, constants, and variables
x
,
y
in
G
F
(
2
)
.
NOT
x
=
1
+
x
,
x
AND
y
=
x
y
,
x
XOR
y
=
x
+
y
,
x
OR
y
=
x
+
y
+
x
y
.
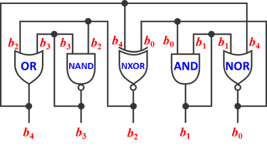
In the figure, label inputs
{
b
n
}
n
=
0
,
…
,
4
∈
G
F
(
2
)
left to right as
b
4
,
b
3
,
b
2
,
b
1
,
b
0
. As per the circuit diagram,
equate the logical gate outputs to the input variables
to produce the following system of equations:
 (
0
)
(
1
)
(
2
)
(
3
)
(
4
)
b
0
=
1
+
b
1
+
b
4
+
b
1
b
4
,
b
1
=
b
1
b
0
,
b
2
=
1
+
b
0
+
b
4
,
b
3
=
1
+
b
2
b
3
,
b
4
=
b
2
+
b
3
+
b
2
b
3
.
Solve by using
G
F
(
2
)
’s multiplicative idempotency (
x
2
=
x
) and additive nilpotency (
x
+
x
=
0
) for simplification (along with its other props).
(
0
)
(
1
)
(
2
)
(
3
)
(
4
)
b
0
=
1
+
b
1
+
b
4
+
b
1
b
4
,
b
1
=
b
1
b
0
,
b
2
=
1
+
b
0
+
b
4
,
b
3
=
1
+
b
2
b
3
,
b
4
=
b
2
+
b
3
+
b
2
b
3
.
Solve by using
G
F
(
2
)
’s multiplicative idempotency (
x
2
=
x
) and additive nilpotency (
x
+
x
=
0
) for simplification (along with its other props).
Sub (0) into (1): b 1 = b 1 b 0 = b 1 ( 1 + b 1 + b 4 + b 1 b 4 ) = b 1 + b 1 2 + b 1 b 4 + b 1 2 b 4 = ( b 1 + b 1 ) + ( b 1 b 4 + b 1 b 4 ) = 0 + 0 = 0 ∴ b 1 = 0 .
Sub b 1 into (0): ( 5 ) b 0 = 1 + b 4 .
Sub (5) into (2): b 2 = 1 + b 0 + b 4 = 1 + ( 1 + b 4 ) + b 4 = ( 1 + 1 ) + ( b 4 + b 4 ) = 0 + 0 = 0 ∴ b 2 = 0 .
Sub b 2 into (3): b 3 = 1 + b 2 b 3 = 1 ∴ b 3 = 1 .
Sub b 2 and b 3 into (4): b 4 = b 2 + b 3 + b 2 b 3 = 0 + 1 + 0 = 1 ∴ b 4 = 1 .
Sub b 4 into (5): b 0 = 1 + b 4 = 1 + 1 = 0 ∴ b 0 = 0 .
Therefore, b 4 b 3 b 2 b 1 b 0 = 1 1 0 0 0 2 = 2 4 1 0 .
So, this is my take for April Fools in 2017.
What is the problem? Well, we see a logic circuit here. The outputs provide the circuit's own inputs, so it's likely that there are contradictions if the outputs are wrong. So let's try to figure out what the outputs should be.
Call the outputs A , B , C , D , E in that order. Remember that ⋅ , + , ⊕ are AND, OR, XOR respectively, and A is the negation of A . For sake of convenience, we'll use 0 , 1 for false and true respectively.
The equations, if you know logic gates , are as follows:
How do we solve it? The self-referential equations are particularly interesting. In fact, the second equation only has one solution. If B = 0 , then B ⋅ C = 0 , but then B ⋅ C = 1 , contradiction. So B = 1 . And now that B = 1 , we have B ⋅ C = 1 , so B ⋅ C = 0 . Since B = 1 , we need C = 0 .
Since we know B , C , we can now deduce A = B + C = 1 . We can then deduce E from the third equation: 0 = 1 ⊕ E , so 1 = 1 ⊕ E , so E = 0 . Finally, this allows us to deduce D : since E = 0 , we have D ⋅ E = 0 , so D = 0 .
Thus, in fact, we have a single solution! It's ( A , B , C , D , E ) = ( 1 , 1 , 0 , 0 , 0 ) . So it is "an answer", even though we're still not sure what we're looking for. But it's worth a try; we have binary outputs, and it says to write the answer in decimal. So we can try reading these values as a binary number 1 1 0 0 0 2 , and interpret it to decimal, giving 2 4 , which is indeed the answer to this problem. Hope you enjoyed it!
This problem is inspired from a more ridiculous, more unfair problem in CodeForces April Fools Contest 2017.
So, yes, this is an April Fools joke. This problem is written in the spirit of puzzlehunt puzzles ; unlike standard problems with clearly defined objective, this problem doesn't tell you what you need to do. (What is "the answer"?) On the other hand, such problems can be satisfying to solve, when you fiddle around with the data you're given and everything suddenly just clicks together. We puzzlehunters call it the a-ha! moment, because that's what you'll probably say when you get the breakthrough. How the problem doesn't need any additional information (because the circuit, the biggest thing that attracts your attention here, does have a unique solution), why there's "in decimal" (because you get a number that is not in decimal, so it serves as a check that you're trying to extract a number and also that number is not originally in decimal)...
Speaking of which, the reason I asked for the decimal number was two-fold: one, it gives you the clue that you'll be getting some number which is not in decimal, and two, this helps making sure that leading zeroes won't be a problem. (Had the answer been something like 00011, you'll see the accepted answer as "11" instead of "00011", which is unclear for people that fail to solve the problem. If it's converted to decimal, you won't care that "3" is missing a leading zero.)