Aquarius Star
A regular hexagon is inscribed in a circle, and 6 lines are drawn to join the vertices, resulting in the Aquarius Star, as shown above.
If the blue area is 120, what is the area of the yellow region?
The answer is 80.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice pictorial image. I see that @Chung Kevin was justifying why these triangles are equal by chasing down side lengths.
Log in to reply
Yeah, it's basically the same proof, but Chung has explained all the steps.
Log in to reply
The lines that Michael drew in help make it clear why the ratio is 6:4. I like this
@Michael Mendrin Beautiful and simplest pattern to think about!
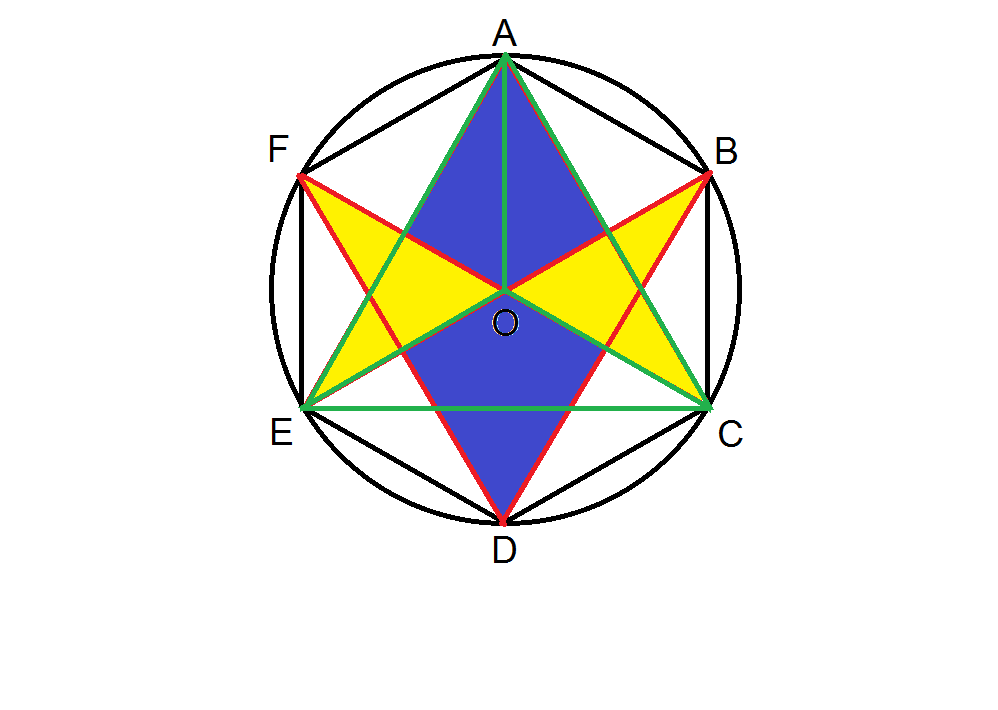
According to the image above, considering triangle A C E , the center O is the centroid of the triangle, making the triangles A O E , E O C , C O A congruent.
And since the inscribed hexagon has each side length equal to the radius, they are 3 rhombhi combining with common vertex O . Thus, the red lines crossing A E & A C are the bisectors for the triangles' bases.
Thereby, each blue kite has the same area as triangle A O E , equal to 3 1 of triangle A C E .
With similarity, each blue kite has an equal area to triangle F O E or B O C .
And similarly, the red and green lines also intersect each other at the centroids of those 2 triangles.
Thus, the yellow area is 3 2 of those triangles, which equals to the blue area.
Finally, the yellow area = 3 2 × 1 2 0 = 8 0 .
And i use sine rules XD
Log in to reply
Well, whatever applies is okay. 😉
Log in to reply
But i got 1 1 0 , i think i miscalulated
I need solution for this
Log in to reply
@Jason Chrysoprase – Honestly, I came up with the question by accident: I was working on prime partition. So I didn't think of the solution. Sorry.
Log in to reply
@Worranat Pakornrat – okay, i'll just wait, just wait :v
Log in to reply
@Jason Chrysoprase – I'm open to your solution though. 😉
Log in to reply
@Worranat Pakornrat – okay, i'm just bad at cubic, need more improvement
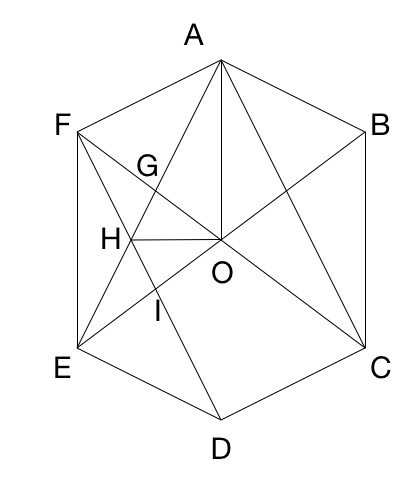
- E I = I O since F D is perpendicular to B E , thus F I is the altitude of equilateral triangle O F E .
- [ G H O ] = [ H I O ] by symmetry and = [ E I O ] since E I = I O and = [ F G H ] by symmetry
- Thus, one yellow quadrilateral is equal in area to 4 small triangles [ G H O ] .
- A G = G E since C F is perpendicular to A E thus C F is the altitude of equilateral triangle A C E .
- [ A G O ] = [ E G O ] since A G = G E , which is equal in area to 3 small triangles.
- Hence, the blue quadrilateral is equal in area to 6 small triangles.
- Thus, yellow : blue = 4 : 6 . So the yellow are is 1 2 0 × 6 4 = 8 0 .
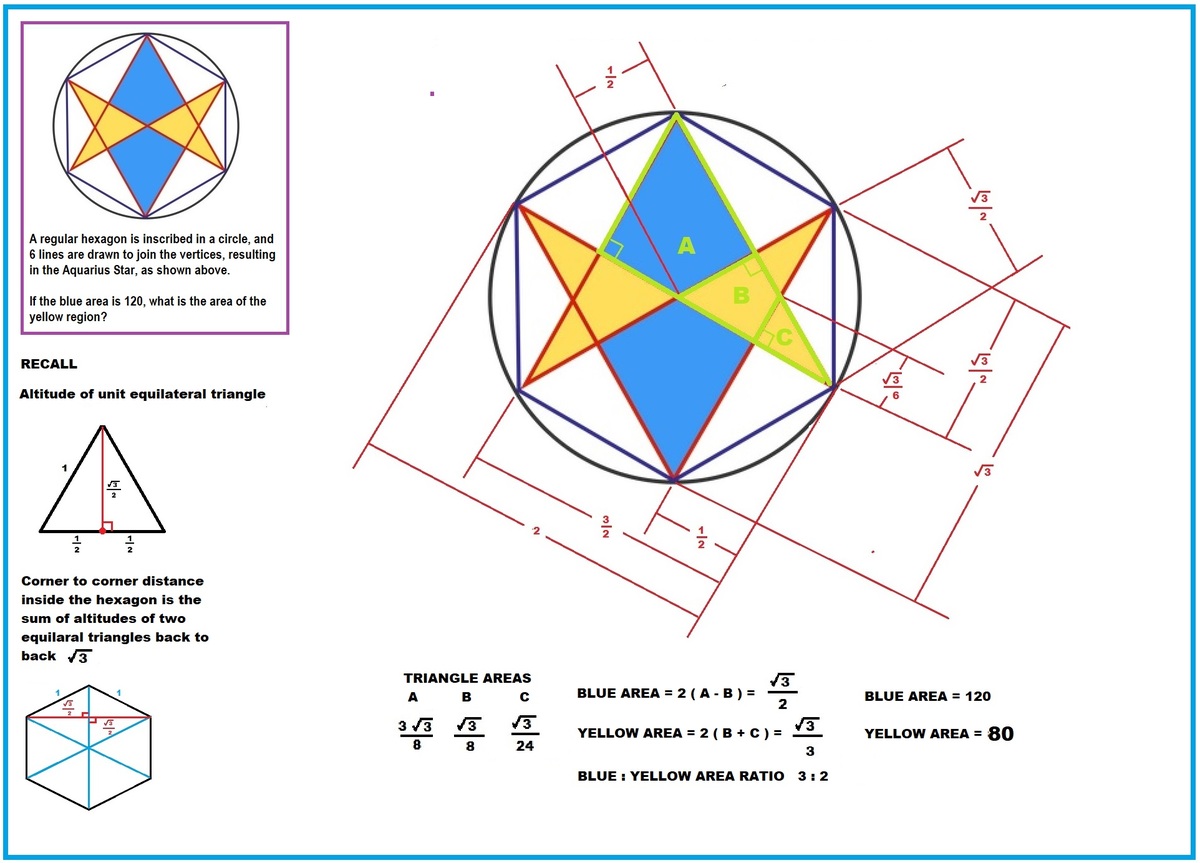
Count the triangles. There are 12 blue triangles, and 8 yellow triangles. Therefore, if blue area = 120, the yellow area = 80.