Archimedean Twins
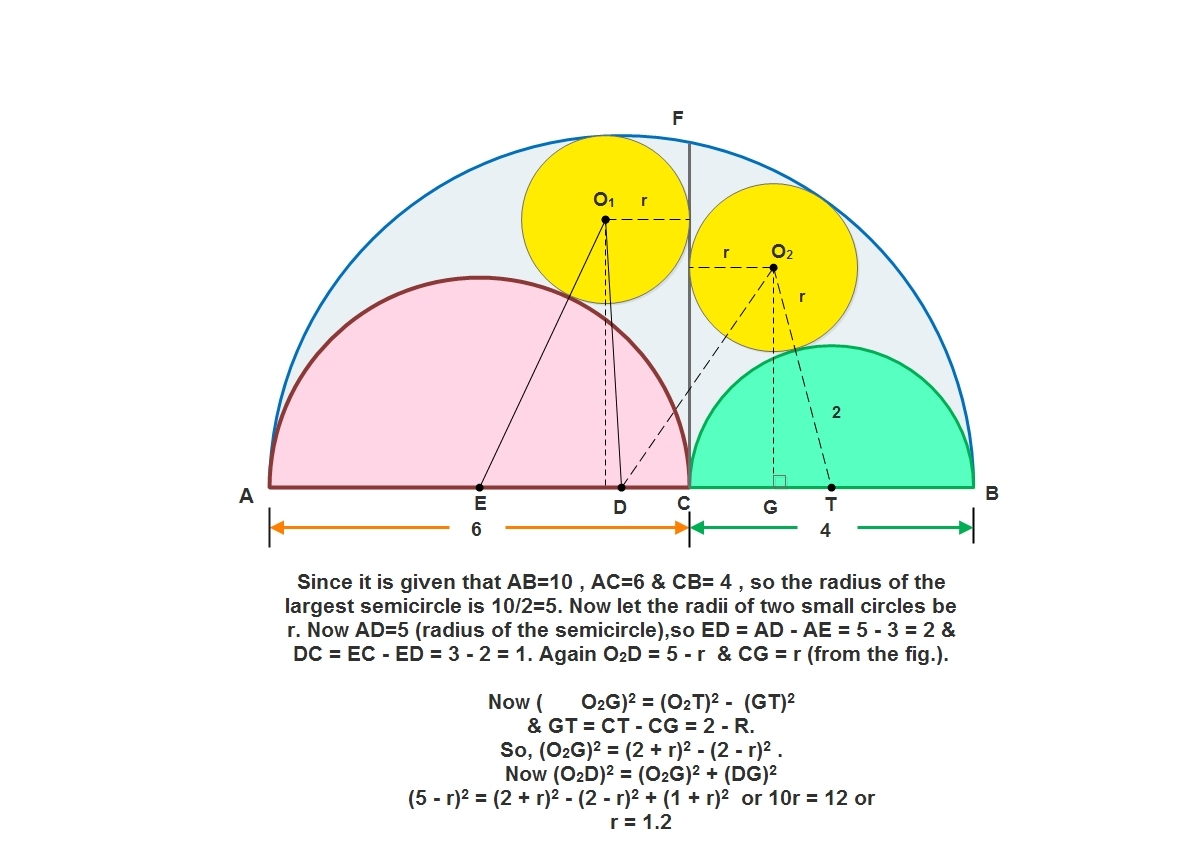
In the figure there are three semicircles of diameters A B , A C , B C and two circles S 1 and S 2 which are touching to the line C F ( C F is perpendicular to A B ). Both circles have same radius and are called Archimedean Twins. Now if A B = 1 0 , A C = 6 and B C = 4 then find the radius of circle S 1 .
The answer is 1.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Centers are, M for pink, O for blue, P for outer.
T is the foot of the perpendicular line.
M
T
=
3
.
P
T
=
1
.
r is the radius of the blue circle, ON is the perpendicular from O
on AB, the diameter of the outer circle.
S
o
N
T
=
r
.
a
n
d
N
P
=
r
−
1
…
.
(
1
)
,
M
N
=
M
T
−
r
=
3
−
r
.
.
(
2
)
Distance between centers are
O
M
=
3
+
r
,
O
P
=
5
−
r
.
.
.
.
.
.
.
(
3
)
F
r
o
m
(
3
)
,
(
1
)
I
n
△
O
N
P
,
O
N
2
=
O
P
2
−
N
P
2
=
(
5
−
r
)
2
−
(
r
−
1
)
2
F
r
o
m
(
3
)
(
2
)
I
n
△
O
M
N
,
O
N
2
=
O
M
2
−
M
N
2
=
(
3
+
r
)
2
−
(
3
−
r
)
2
∴
(
5
−
r
)
2
−
(
r
−
1
)
2
=
(
3
+
r
)
2
−
(
3
−
r
)
2
.
S
o
l
v
i
n
g
r
=
1
.
2
Beautiful solution! Sir, I have uploaded an image with your point labels. Just append ![Imgur] on left of this and insert in your solution (https://i.imgur.com/hDMuZKb.png)
Log in to reply
Thanks a lot, Ujjwal. How do you do it. We can come to the same conclusion if the right side semicircle is used. That is better since we do not have N and P so near.
Log in to reply
My pleasure sir! I used the CAD software - MicroStation - to create that. As for the problem, out of curiosity I solved it symbolically, taking outer circle R, inner circles r1, r2 and the Archimedian circle as r. Did the derivation pretty much like you did and the result was r = R r 1 r 2
Log in to reply
@Ujjwal Rane – Yes. This is the formula given for Archimedean circle . You may give the proof so that others can know. That is what I have requested Rifath Rahman.
Log in to reply
@Niranjan Khanderia – Yes, in fact i was in the process of writing it. Only not sure if I should post it as a response to this question or a separate Note. Probably a Note could reach more users?
Log in to reply
@Ujjwal Rane – I agree. Note would better serve our purpose.
Log in to reply
@Niranjan Khanderia – Posted a note on Proof of expression for radius of Archimedes's twin circles
Sir, could you please review and give your suggestions?
Can you tell me how you know N is to the left of P? why can't it be to the right of P? thanks!!!
where r is the radius of the circle.
awesome way to solve the prob.
I too was thinking of giving alternate solution from the right side. Can you please give how you generated the file you have down loaded ? I am not able to get this size from M.S. Accessories-Paint. Thanks.
Log in to reply
I have used a drawing software named Edraw. Which is a very good multi designing software. I will suggest you to use it.
Let a=AC=diameter of first inner semi-circle,b=diameter of second inner semi-circle and diameter of Arcimedean circle be d,we know that d={(ab)/(a+b)}={(6 *4)/(6+4)}=24/10=2.4,so radius of Archimedean circle is 2.4/2=1.2
It is much better than mine. We can use Archimedean circle formula dirctly as you have done. But a proof would be welcome.
Log in to reply
Actually it came from the way you did it,you can see it in detail in wikipedia,search Archimedian twin circle
Log in to reply
Thanks. I did see it before I wrote my comment. I thought it would help others.
The radius r of Archimedean twin circles inscribed by three semicircles of radii a , b & a + b & having shared diameter, is given by the general formula
r = a + b a b
As per given question, setting a = 3 & b = 2 in above general formula , radius of twin circles
r = 3 + 2 3 ⋅ 2 = 5 6 = 1 . 2