Archit's Challenge 2

Algebra Level 4

Given that $a,b$ and $c$ are roots to the equation $x^3-3x^2+8x-2 = 0$ , find the value of $(9+a^2)(9+b^2)(9+c^2)$ .

The answer is 634.

3 solutions

Archit Agrawal
Nov 28, 2015

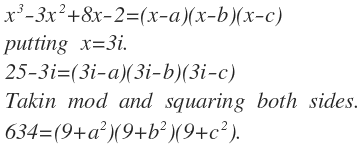
Wow! Very unusual approach! Thanks for sharing!

Pi Han Goh - 5 years, 6 months ago

i multiplied f(3i) with f(-3i)

aryan goyat - 5 years, 6 months ago

nice approach.

neelesh vij - 5 years, 6 months ago

challenge 4 is that question is question which you gave me first time

aryan goyat - 5 years, 6 months ago

Nice way!!

Dev Sharma - 5 years, 6 months ago

Archit, you have already assumed that all the three roots of the given polynomial are real. ( As in the $3^{rd}$ step, while taking modulus, you have treated $a,\,b$ and $c$ as real parts. ). But, this is not possible as at least one root has to be complex. How can you justify the $3^{rd}$ step ? Rectify me if I'm wrong.

Aditya Sky - 5 years, 3 months ago

This works because the modulus operator has been used in the following sense:

$\left| f\left( x \right) \right| =\quad f\left( ix \right) .f\left( -ix \right)$

Aditya Dhawan - 4 years, 7 months ago

I got it. But, as far as I know, for $x\,\in\, \mathbb{C}$ , $|x|$ is defined as $\sqrt{(\Re(x))^{2}+(\Im(x))^{2}}$ .

Aditya Sky - 4 years, 7 months ago

@Aditya Sky – It is. I am just saying the operation he has performed (and called as modulus) is the former.

Aditya Dhawan - 4 years, 7 months ago

Unusual indeed. I did a much longer method

Shreyash Rai - 5 years, 6 months ago

Please share your method also.

Archit Agrawal - 5 years, 6 months ago

Akshat Sharda
Nov 28, 2015

I used a much longer approach.

$(9+a^2)(9+b^2)(9+c^2) \\ 729+81(a^2+b^2+c^2)+9((ab)^2+(bc)^2+(ca)^2)+(abc)^2 \\ \text{Now using Newton's Sum and Vieta's formulae will give us:} \\ 729+81(-7)+9(52)+4=\boxed{634}$

Thanks for posting your method.

Archit Agrawal - 5 years, 6 months ago

Aditya Sky
Mar 3, 2016

As $a^{2}+9, b^{2}+9$ and $c^{2}+9$ are symmetric functions of the roots of the given polynomial, so we can transform the given polynomial into a polynomial whose roots are of the form $a^{2}+9$ . The required value would then be equal to the product of roots of that polynomial which can be determined using Viete. The transfromed polynomial is $x^{3}-20x^{2}+169x-634$ . Using this polynomial, we can also figure out the value of expressions like :- $1.) (a^{2}+9)+(b^{2}+9)+(c^{2}+9)$ $2.) (a^{2}+9)(b^{2}+9)+(b^{2}+9)(c^{2}+9)+(c^{2}+9)(a^{2}+9)$

Archit's Challenge 2

The answer is 634.

3 solutions

I used a much longer approach.

0 pending reports