Archit's Challenge 3
Given
f ( x ) = x 1 3 + 2 x 1 2 + 3 x 1 1 + 4 x 1 0 + ⋯ + 1 3 x + 1 4 ,
denote
N = f ( a ) × f ( a 2 ) × f ( a 3 ) × ⋯ × f ( a 1 4 ) ,
where a = cos ( 1 5 2 π ) + i sin ( 1 5 2 π ) .
Then what is the value of M such that N M 1 = 1 5 ?
The answer is 13.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
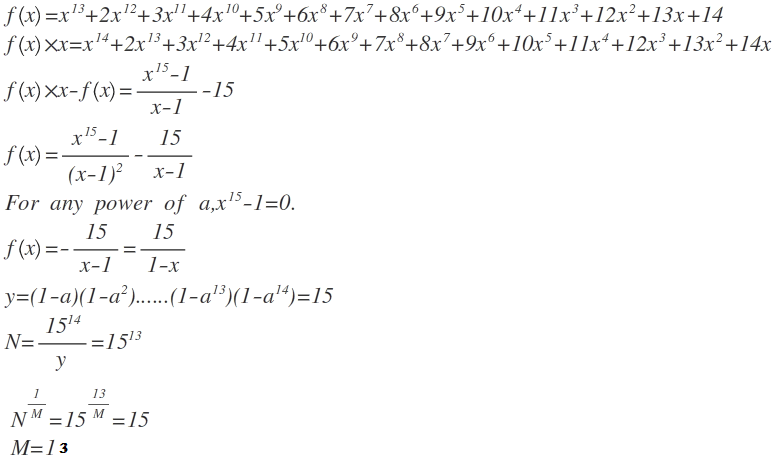
My solution was very similar. Also, do you happen to be related to Manindra Agrawal, the mathematician that helped develop the AKS primality test? Or is Agrawal just a common name?
would u mind explaining how you got -15 in the 3rd statement ,i was getting -14 :(
Log in to reply
plz tell , i was doing the same but continuously getting -14 there :(
I cannot up vote as you include statements that are not explained or not relevant to solution wanted.
Log in to reply
Tell me which step needs to be explained.
Log in to reply
I think he's wondering where the b, c, and d came from.
Log in to reply
@Jason Martin – I wrote a question which included b,c and d but the question was changed by brilliant.
All right, I read that changes were made and please ignore my comment of not relevant. Please do not mind to explain as it is not directly obvious. I have checked that it is indeed correct but how did you get ( 1 − a ) ( 1 − a 2 ) . . . ( 1 − a 1 3 ) ( 1 − a 1 4 ) = 1 5 ?
Log in to reply
@Lu Chee Ket – Since we are dealing with the 1 5 X t h root of unity here, it satisfies the equation x X 1 5 − 1 = 0 . We want the product k = 1 ∏ 1 4 ( 1 − α k ) where α 1 5 − 1 = 0 (excluding α = 1 ). A simple switch x = 1 − y will make the equation ( 1 − p ) 1 5 − 1 = 0 . The product we want is equivalent to k = 1 ∏ 1 4 p k which can be shown equal to 15 by partially expanding using the binomial theorem and applying Vieta's formula.
Log in to reply
@Aditya Malusare – I am sorry that I don't know about Vieta's formula.
@Lu Chee Ket – a is 15th root of unity and it is property of this product.
Log in to reply
@Archit Agrawal – Well, I did't need to do the mathematics you have shown here but I got to know that the answer was 13. Just believe me that the answer is 13. Next time when you meet this question, just tell me that the answer is 13. This is our knowledge.
this is similar to archit sir, but use of a little calculus and further elucidation. the eqn can be written as f ( x ) = n = 0 ∑ 1 4 ( ( 1 4 − n ) x n ) = 1 4 n = 0 ∑ 1 4 ( x n ) − n = 0 ∑ 1 4 ( n x n ) by gp n = 0 ∑ 1 4 ( x n ) = x − 1 x 1 5 − 1 d.w.r.x and multiply by x: n = 0 ∑ 1 4 ( n x n ) = x − 1 1 5 x 1 5 − ( x − 1 ) 2 x 1 6 − x so the expression is the same thing as f ( x ) = 1 4 x − 1 x 1 5 − 1 − x − 1 1 5 x 1 5 + ( x − 1 ) 2 x 1 6 − x we see that a is a primitive 15th root of unity. if you dont know much about them, if y is a nth root of unity≠1, then. y n = 1 o r y n − 1 + y n − 2 + . . . + y + 1 = 0 also, if y is a nth root of unity, so is y k for ints k knowing this property, a 1 5 = 1 p ( a ) = a 1 4 + a 1 3 + . . . + a + 1 = 0 so, f becomes f ( a ) = 1 4 a − 1 a 1 5 − 1 − a − 1 1 5 a 1 5 + ( a − 1 ) 2 a 1 6 − a = 1 − a 1 5 so we are just looking for ( 1 − a ) ( 1 − a 2 ) ( 1 − a 3 ) ( 1 − a 4 ) . . . ( 1 − a 1 4 ) 1 5 1 4 we know that a polynomyial can be expressed as ∏ ( a r g u m e n t − r o o t s ) . since a, a 2 .. are roots of p, p ( 1 ) 1 5 1 4 = 1 5 1 5 1 4 = 1 5 1 3
Wow! This is great! ThankYouuu