Pink Valentine's Day Triangle
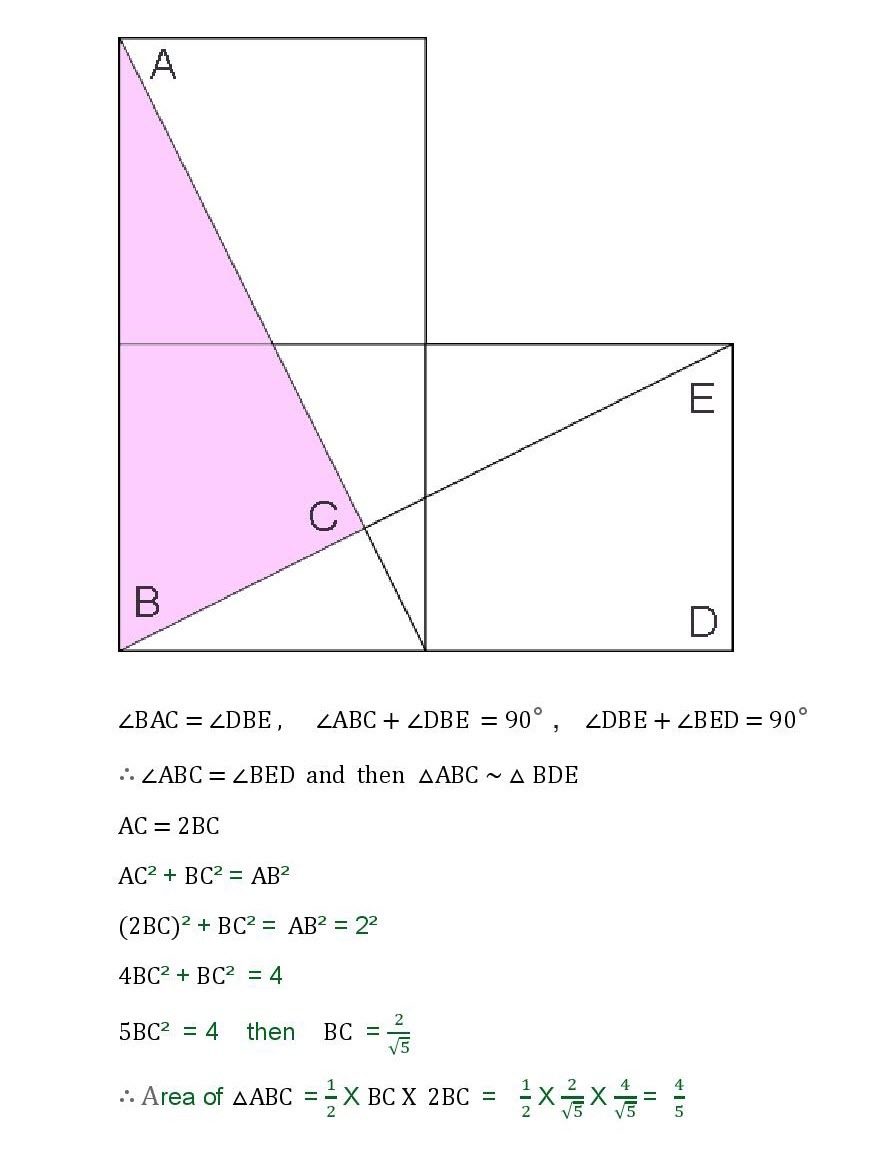
In the following picture, there are three squares of side length 1.
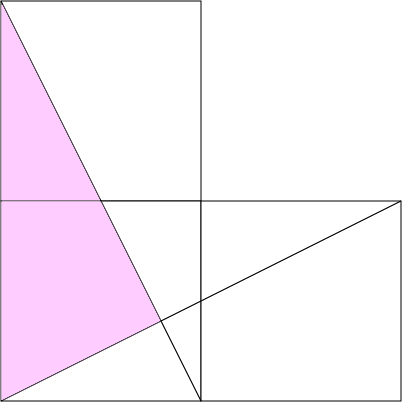
Find the area of the pink triangle.
Source: University of Lincoln 2015.
The answer is 0.8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
Nice solution, I did the same.
I used the same method... Really, understanding geometry through algebra is a powerful tool.
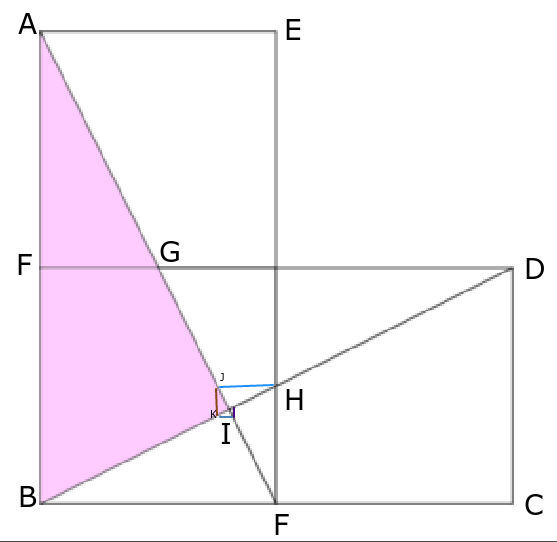
The area of the pink triangle can be written as...
ΔABI = ( ΔABF - ( ΔBFH - ( ΔFHJ - ( ΔHJK - ............ ∞ ) ) ) )
ΔABI = ( 1 - ( 4 1 - ( 1 6 1 - ( 6 4 1 - ......∞ ) ) ) )
ΔABI = 1 - 4 1 + 1 6 1 - 6 4 1 + ......∞
This is an infinite geometric series.
Let a=1, Common ratio r = - 4 1 .
ΔABI = 1 − r a = 1 − ( − 1 / 4 ) 1 = 5 4
Area of pink triangle (ΔABI) = 0.8
Nice solution. Its cool.
Nicest solution ever
It can also be done using trigonometry
Log in to reply
yep... if the area of each square is 1, the squares must be 1 long.
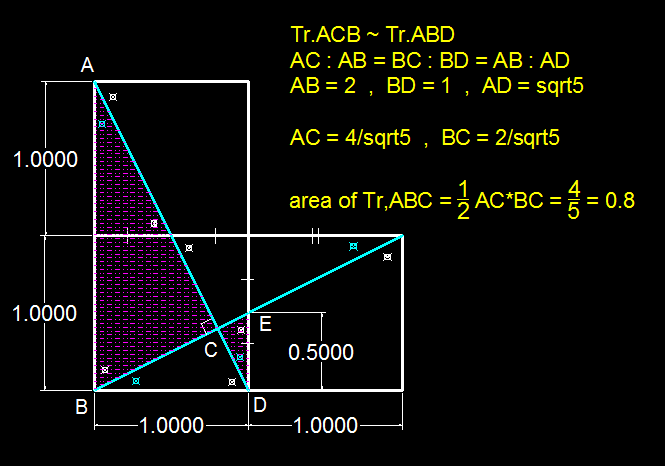
Considering the triangle ABD, a right angled triangle with BD 1 long and AB 2 long, tan A = 0.5 therefore A = 26.57 degrees . It can be seen that BE extending to the right hand side of the L shape intersects AD at right angles.
ABC is a right angled triangle with the hypotenuse AB, which is 2 long. Since we know A = 26.57 degrees and sin 26.57 = 0.4472 we can determine BC as 0.8944, and AC as 1.7889.
The area of ABC is therefore 0.5 x 0.8944 x 1.7888 = 0.8
(sorry, no luck doing the LaTeX tags!)
Log in to reply
How BC can be 1 when BD is 1.
Log in to reply
@Muhammad Arslan Maan – When Andy is being thick and mixing up his sins and tans... now fixed.
yes, exactly...
Alternative answer not using multiple significant figures...
For ABD, we know BD = 1 and AB = 2, therefore AD = 5^0.5
For BCD, we know BD = 1, and the internal angles are the same as ABD - angle B of BCD is the same as angle A of ABD - so cos B = 2/5^0.5. Taking cos B = BC/BD, cos B = BC/1 and therefore BC = 2/5^0.5.
To calculate AC, take AB^2 = AC^2 + BC^2
2^2 = AC^2 + 4/5
16/5 = AC^2
AC = 4/5^0.5
and finally, the area of ABC = (0.5)(BC)(AC) = (0.5)(2/5^0.5)(4/5^0.5) = 4/(5^0.5)(5^0.5) = 4/5 = 0.8
Actually, I found a completely different solution avoiding trigonometry.
The area of triangle ABD is 1, and its hypotenuse (AD) is 5^0.5
If we take the hypotenuse as the base of ABD, the height (BC) is calculated as:
Area = (0.5)(BC)(AD) 1 = (0.5)(BC)(5^0.5) 2/5^0.5 = BC
AB^2 = BC^2 + AC^2, therefore: 2^2 = 2/(5^0.5)^2 + AC^2 4 = 4/5 + AC^2 16/5 = AC^2 AC = 4/5^0.5
Area of ABC is therefore (1/2)(2/5^0.5)(4/5^0.5) = 8/10 = 0.8
Alternatively, as someone else posted, the hypotenuse of ABD is 5^0.5 and the hypotenuse of ABC is 2, and they are similar triangles.
If the hypotenuses are in the ratio 2:5^0.5 then the areas are in the ratio 4:5, or 0.8.
I did the same.
The pink triangle and the bottom triangle are similar with hypotenuse 2 and 1 respectively. As such, the length of their sides are in the ratio of 2:1 and therefore, the areas in the ratio of 4:1. As the combined area of these two triangles is 1, the area of pink triangle would be 4/5.
Wow, it's very sad that this isn't the top solution!
Ha, I did that, too! Well, I compared the bases, anyway.
I did exactly the same. Quite simple!
2 1 2 2 S i n ( A r c T a n ( 2 1 ) ) C o s ( A r c T a n ( 2 1 ) ) = 5 4
Trig identities:
S
i
n
(
A
r
c
T
a
n
(
x
)
)
=
x
2
+
1
x
C
o
s
(
A
r
c
T
a
n
(
x
)
)
=
x
2
+
1
1
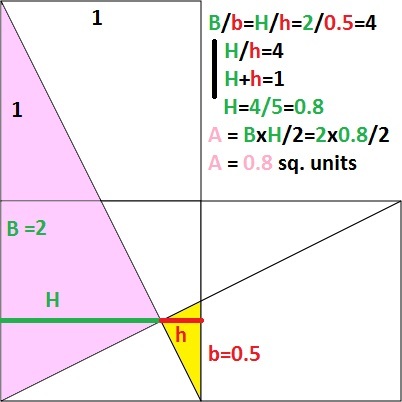
2nd approach, subtracting similar triangle from larger 1 × 2 triangle
( 2 1 1 ⋅ 2 ) − ( 1 2 + 2 2 1 ) 2 ( 2 1 1 ⋅ 2 ) = 5 4
Great solution. I didn't think of this.
Log in to reply
Such simple task must not to be found here!!!
I integrated (-2x+2-x/2)dx from 0 to 4/5 and I obtained the correct answer: 4/5.

Comparing pink to green:
Ratio of hypotenuses: 2: 5
Ratio of areas: 4:5
Area of green: 1
Area of pink: 4/5
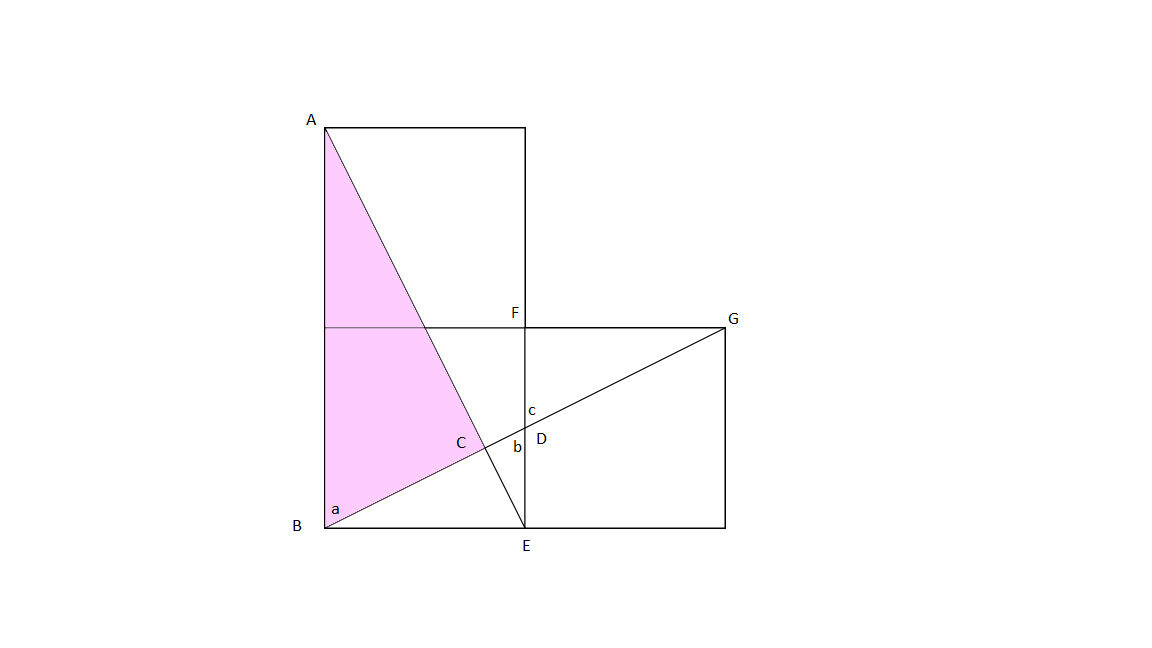
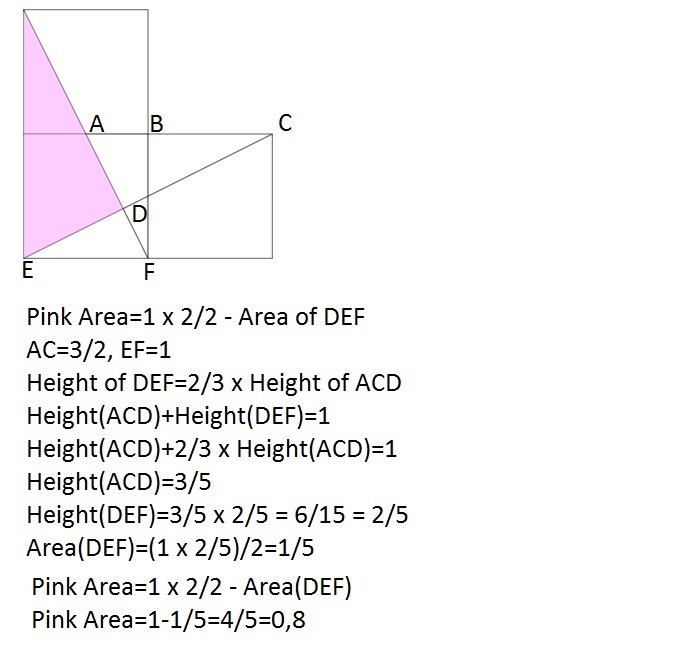
All 3 triangles ABC, CDE and FDG are right triangles, and so must be similar if they also share one other angle. Angles c and b are clearly equal. Angles a and b are also equal as AB and EF are parallel. Therefore ABC and DFG are similar and so ∣ A C ∣ ∣ B C ∣ = ∣ F G ∣ ∣ F D ∣ = 0.5. The length of the hypotenuse of ABC is 2 and so by Pythagoras |BC| = 5 2 and the area of ABC is 0.8
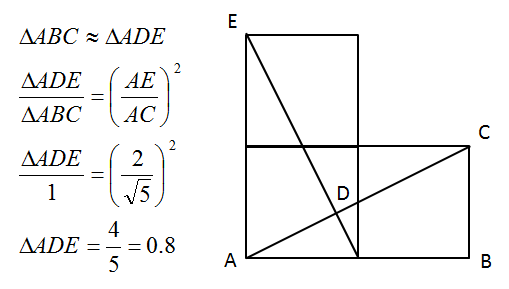
Let B be the origin, B A lie along the positive y -axis and the positive x -axis lie to the right of B .
Then B C lies along the line y = 2 1 x and C A lies along the line y − 2 = − 2 x ⟹ y = − 2 x + 2 .
The point of intersection of these two lines is then C , the x -coordinate of which is such that
2 1 x = − 2 x + 2 ⟹ 2 5 x = 2 ⟹ x = 5 4 .
With B A being the base of Δ A B C , this triangle then has a base of length 2 and a height of 5 4 , and thus has an area of 2 1 ∗ 2 ∗ 5 4 = 5 4 = 0 . 8 .