Are they equal for sure?

Relevant wiki: Using the Quadratic Formula

$\frac{m^{2}+n^{2}}{mn}=\frac{m}{n}+\frac{n}{m}$ .

Let $\frac{m}{n}=x$ . It is clear that $x$ can be any positive rational number except $1$ due to the 'distinct' constraint.

We now have $x+\frac{1}{x}=p \Rightarrow x^{2}-px+1=0$ where $p$ is an integer. Quadratic formula gives:

$x=\frac{p \pm \sqrt{p^{2}-4}}{2}$

Clearly, $p^{2}-4$ must be a perfect square for $x$ to be rational. Since all consecutive perfect squares are separated by an odd number, we must have that $p^{2}$ and $p^{2}-4$ have a difference being the sum of some number of consecutive positive odd numbers. It is easy to see that the only such sum is $1+3$ which gives $p^{2}=4$ or $p= \pm 2$ .

This results in $x+\frac{1}{x}= \pm 2$ or $x= \pm 1$ , both of which we can reject due to the constraint that $m$ and $n$ are positive and distinct.

Hence, $\boxed{0}$ solutions exist

Relevant wiki: Greatest Common Divisor

Any solution $m, n$ induces a solution $p = m/gcd(m,n), q = n/gcd(m, n)$ where $p$ and $q$ are coprime.

Then $p | p^2 + q^2$ so $p | q$ so $p = 1$ , and symmetrically $q = 1$ which implies that $m$ and $n$ were not distinct.

Relevant wiki: Greatest Common Divisor

Set $d= \gcd(m,n)$ and $m=m'd, n=n'd$ . Then we know $m'$ and $n'$ are coprime. Note that since $m^2 +n^2=(m+n)^2-2mn$ , we know $mn | m^2+n^2 \rightarrow mn | (m+n)^2$ , and then canceling the $d^2$ , we get $m'n' | (m'+n')^2$ . Since $m'+n'$ is coprime to both $m'$ and $n'$ , we know this can only be possible when $m'=n'=1$ . Given $m \ne n$ , we know there are no solutions.

Let $A= \frac{m^2+n^2}{mn}$ where $A$ is an integer:

We are going to prove that $A$ is always not an integer for all $m \neq n$

$\Rightarrow A= \frac{m}{n} + \frac{n}{m}$

For $A$ to be an integer, both $\frac{m}{n}$ and $\frac{n}{m}$ must also be integers

So:

$\begin{cases} n|m \\ m|n \end{cases}\Longrightarrow m=n$

But that's a contradiction to $m \neq n$

Therefore, $A = \frac{m^2+n^2}{mn} \notin \mathbb{Z} \Rightarrow \boxed{mn \nmid m^2+n^2 }$ for all $m \neq n$

Given that,

• $m$ and $n$ are distinct positive integers.

Assume $m$ and $n$ can be odd or even. In this way, any pair wouldn't work. Let's prove that.

Step 1: $Odd \times Odd = Odd$ $~ ~ ~~ ~ ~~ ~ ~~ ~ ~~ ~ ~~ ~ ~~$ $3 \times 5 = 15$

Step 2: $Odd^2 + Odd^2 = Even$ $~ ~ ~~ ~ ~~ ~ ~~ ~ ~~ ~ ~~ ~ ~~$ $3^2 + 5^2 = 34$

(Even, odd) and (Odd, even) are also allowed in the first step.

$\text{\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_}$

Step 1: $Even \times Even = Even$ $~ ~ ~~ ~ ~~ ~ ~~ ~ ~~ ~ ~~ ~ ~~$ $2 \times 4 = 8$

Step 2: $Even^2 + Even^2 = Even$ $~ ~ ~~ ~ ~~ ~ ~~ ~ ~~ ~ ~~ ~ ~~$ $2^2 + 4^2 = 20$

(Even, odd) and (Odd, even) are also allowed in the first step.

Now, we have (15 , 34) and (8,20)

According given conditions, we need to divide it.

$34 \div 15 = 2.26$ $~ ~ ~ ~ ~ ~ ~$ $20 \div 8 = 2.5$

$(m,n)$ has infinitely many values, but it is true that they can be odd or even. Which satisfies this method.

Hence $mn ∤ m^2 + n^2$ .

We can rewrite the expression $m^{2}+n^{2} \text{ as } (m+n)^{2} -2mn$ .

Then we would just have to find number $m,n$ such that $mn| m+n$ .

it can be easily seen that there are no such positive number.( $\text{ as } mn \text{ becomes much larger as compared to } m+n .$ )

If a solution exists and m and n have a common factor, divide both sides by this factor squared, so that m and n are now co-prime and m^2 = 2kmn - n^2. The right hand side is a multiple of n and the left hand side is not, so this is not possible. The only exception is if n = 1, in which case n^2 = 2kmn - m^2, so 1 = 2km -m^2, which is possible only if m = 1, since the right hand side is a multiple of m.

Using contradition:

Assume $m^2+n^2 = 2kmn$

Solve for m: $m = kn \pm n\sqrt{k^2-1}$ (*)

k, n, kn are integers. So $n\sqrt{k^2-1}$ is integer. $k^2-1$ is integer as well. For m to be integer, we need $k^2-1$ to be perfect square. So $k^2-1 = a^2$ where a is integer. Rewrite it as $k^2 - a^2 = 1$ . The farther apart k (k>a) and a are the farther their difference from 1 ( $\ge$ 1). In hope to have $k^2 - a^2 = 1$ , take closest k and a, k=a+1, then $k^2 - a^2 = (a+1)^2 - a^2 = 2a+1 = 1$ . So a = 0, k = 1. From (*), it follows that m = n. Contradition! So no distinct m and n exist.

Both m and n have to be at least even for $\frac{m^2+n^2}{mn}$ to be an integer.

So one could assume that m = 2p and n = 2q with p, q belonging to N*.

So $\frac{m^2+n^2}{mn}$ = $\frac{4p^2+4q^2}{4pq}$ = $\frac{p^2+q^2}{pq}$ . For it to be true, you need both p and q to be even numbers again, which by luck could be the case, that would thus lead to the same loop, again. Eventually, this will not be true anymore after a finite number of loops, thus this problem has no solution.

I took a simple view: The result of the division = m/n + n/m. If m and n are distinct then one of those fractions is <1 so there is necessarily a remainder.

Let $gcd(m,n)=d$ and $m=dm_0$ and $n=dn_0$

$\frac{m^2+n^2}{mn}$

$=\frac{m_0^2+n_0^2}{m_0n_0}$

$=\frac{m_0}{n_0}+\frac{n_0}{m_0}$

Since these two terms are reciprocals to each other and in its simplest form, the sum cannot be an integer unless both are equal.

$\therefore m_0=n_0 \iff \boxed{m=n}$

Definition: For a prime $p$ and natural number $x$ we define $ord_p(x)$ to be the largest non-negative integer $e$ such that $p^e$ divides $x$

If $m, n$ are distinct then there is a prime $p$ such that $ord_p(m) \neq ord_p(n)$ . So we have $ord_p(mn) = ord_p(m) + ord_p(n) > 2 \min \{ord_p(m), ord_p(n) \} = ord_p(m^2 + n^2)$ . However if $mn$ divides $m^2 + n^2$ then $ord_p(mn) \le ord_p(m^2 + n^2)$ . So there are no distinct positive numbers $m, n$ for which $mn$ divides $m^2 + n^2$ .

We require $m^2 + n^2 = Imn$ where $I$ is an integer. This is a quadratic equation with solution $m = 0.5n \left( I \pm \sqrt{I^2 - 4} \right)$ . For $m$ and $n$ to be integers, $\sqrt{I^2 - 4}$ must be an integer. The only solution to this is $I = 2$ which is the trivial solution $m = n$ not allowed by the problem.

Because simply, mn < m^2 + n^2

I guess using a spreadsheet is 'cheating' ? (Took about one minuit to see the pattern)

I have another approach for the solution.

Consider $\dfrac{m^2 + n^2}{mn}.$

$\dfrac{m^2 + n^2}{mn} = \dfrac{m}{n} + \dfrac{n}{m}$

Now, if this has to belong to integers and that too, even, then $m \leq n$ and $n \leq m$ which gives n = m (non - distinct integers). Hence there does not exist any integers which can give the required result.

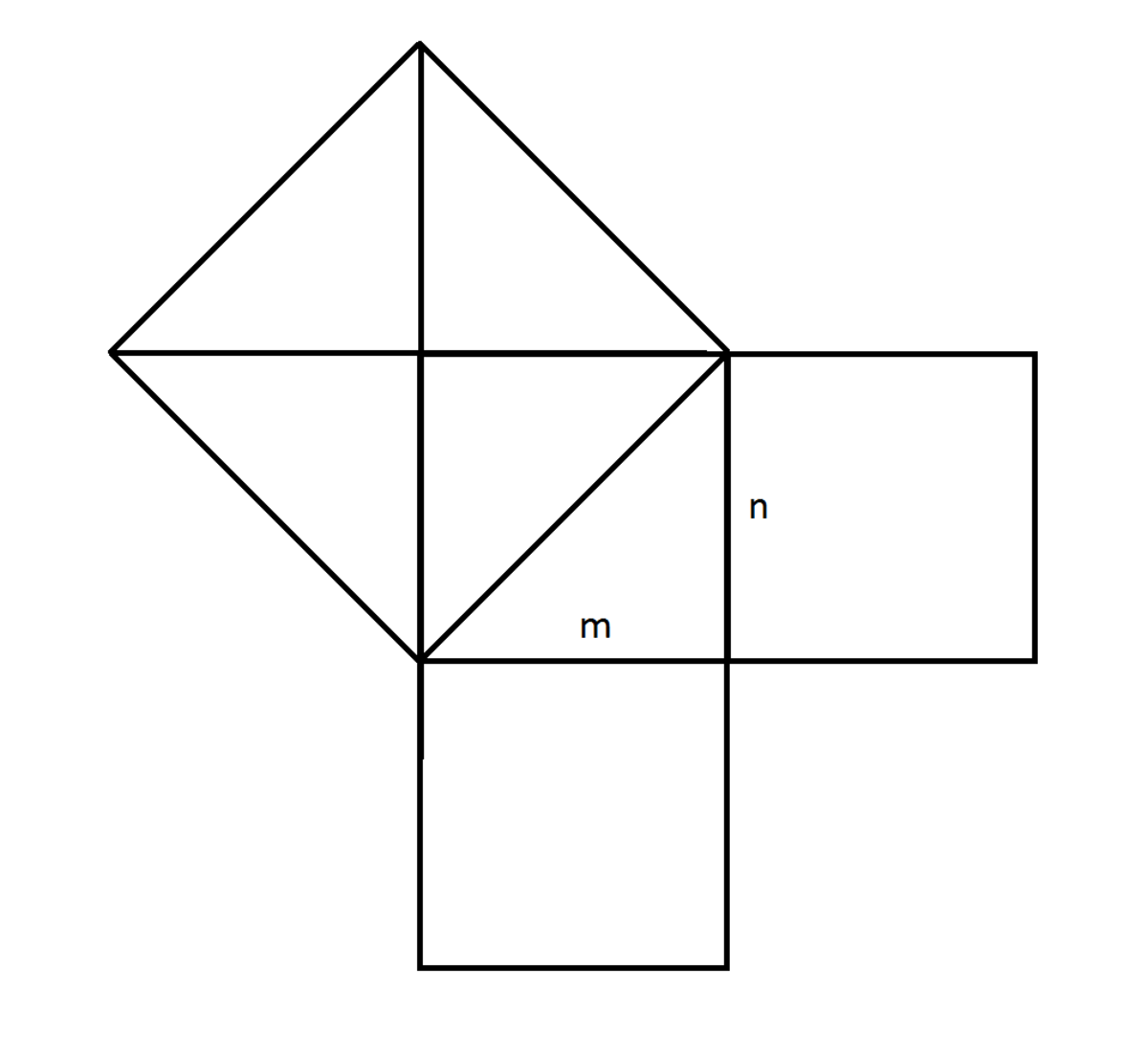
Let m and n be sides of a right-angle triangle. If m=n, m*n divides m^2 + n^2 (in other words, the area of hypotenuse squared) neatly into 2.

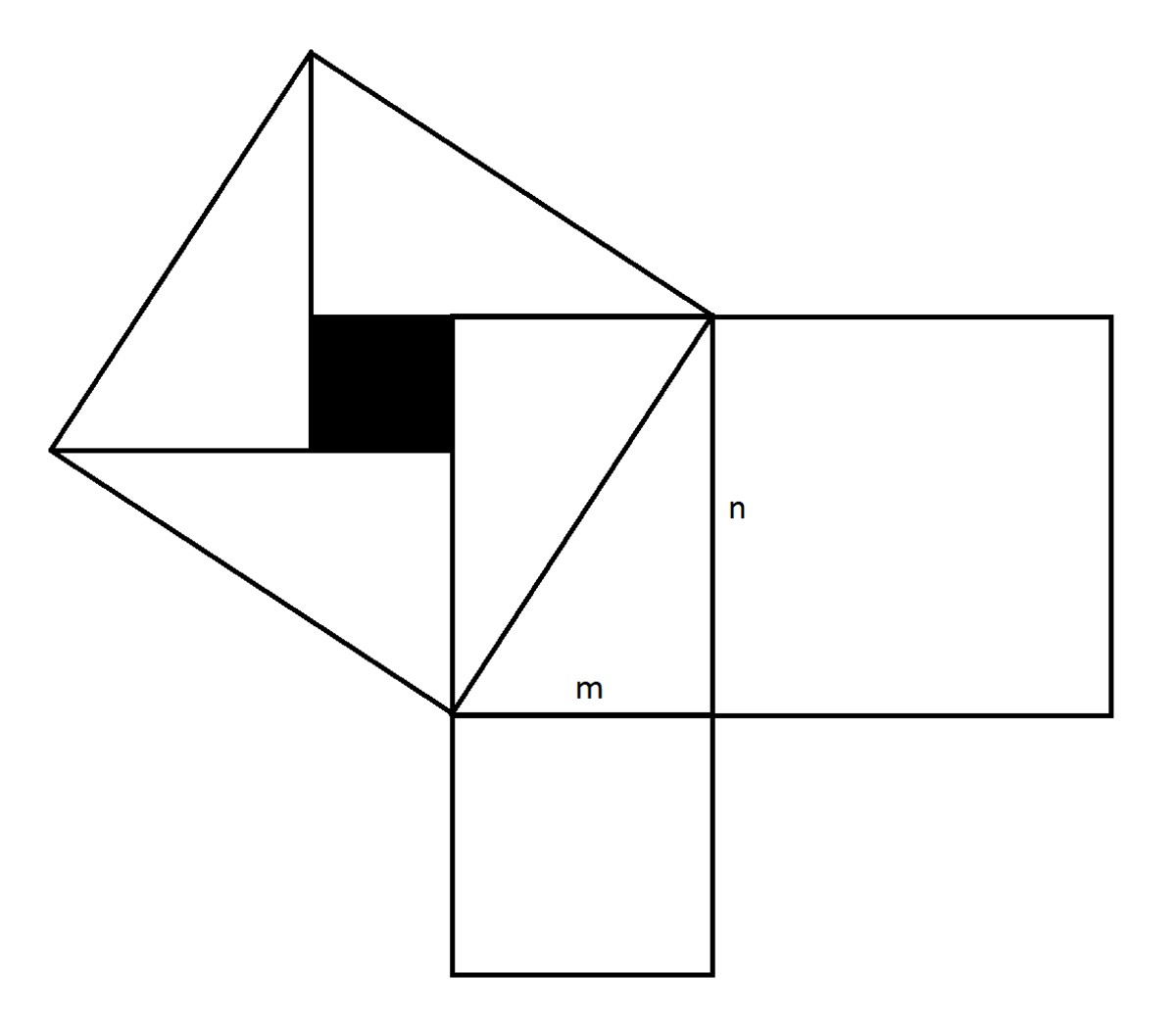
For any other case where (n>0; m>0; n!=m), always 2mn < m^2 + n^2

The problem requires that m!=n AND z m n = m^2 + n^2, however the right side solution can only be solved if m=n, and z=2; OR m=n=0. Therefore the answer is that there aren't distinct positive integers that fit the problem. Comments encouraged - visual solution was the first thing that came to mind, however I realize it does not count as a mathematical proof. Would be great if someone could elaborate on a geometric proof.

We have that $mn | m^2 + n^2$ with $m \neq n$ , which is the same as saying that, for some integer $k$ ,

$m^2 + n^2 = kmn$

$\dfrac{m^2+ n^2}{mn} = k$

And finally $\dfrac{m}{n} + \dfrac{n}{m} = k$

We know $k$ is an integer, and the only integer solution to $x + \frac{1}{x} = k$ with rational $x$ is $k = 2$ , which implies

$m = n$ , a contradiction.

Corrections are welcome

If mn | $m^2 + n^2)$ , then $m^2 + n^2)$ = kmn for some positive integer k. Then m(kn - m) = $n^2$ . This shows that m | $n^2$ . Similarly n | $m^2$ . Let p be a prime dividing m, then p | $n^2$ , then this shows that p | n. Simiarly if p | n, then p | m. So, since m and n are positive, let m = $p_1^{k_1}………….p_r^{k_r}$ , and n = $p_1^{l_1}………….p_r^{l_r}$ . If $p^j$ || m and $p^t$ || n, then m = $p^j$ x and n = $p^t$ y, where (p, x ) - (p, y) = 1. Then $p^{2j}x^2$ + $p^{2t}y^2$ =k $p^{j + t}$ xy. If j < t, then $x^2$ + $p^{2t - 2j}y^2$ = k $p^{t- j}$ xy. This shows that p | $x^2$ and therefore p | x which is a contradiction since by definition (p , x) = 1. Similarly if t < j, we again reach a contradiction. Therefore j = t, and m = n.

If m2+n2 is evenly divisible by mn then

m2+n2 = 2mn

Which means m2+n2 - 2mn = 0 (m - n)2 = 0.

This is only possible if m = n

Suppose this is true. Then there an integer $k$ such that $m^2 + n^2 = kmn$ . Then dividing by $n^2$ (which is allowed, since $n > 0$ ) gives the quadratic equation $\left(\frac{m}{n}\right)^2 - k\left(\frac{m}{n} \right)+1 = 0$ . Now solve for $\frac{m}{n}$ to get $\frac{m}{n} = \frac{k \pm \sqrt{k^2 -4}}{2}.$ Since $m$ and $n$ are distinct, suppose that $m<n$ . Then $\frac{m}{n} < 1$ , from which it follows that $\frac{k \pm \sqrt{k^2 -4}}{2} < 1.$

From the last equation, it must be true that both $k < 2$ and $k > 2$ ; that is, no such $k$ exists. Supposing that $m > n$ gives a similar contradiction.

NO SOLUTION AS YET, JUST A COMMENT! When the question says .... evenly divides m^2 + n^2 should it read 'exactly divides .....'. Regards, David

The key information is that $m$ and $n$ are distinct . Let $n = m+k$ for integer $k\neq 0$ .

It follows $m^2+km$ and $2m^2+2km+k^2$ are the numbers. Inspecting, there is nonzero remainder, $k^2$ .

Set up the equation: m^2+n^2=amn where a is some integer. (Since m^2+n^2 is an integer multiple of mn if mn divides). Dividing by mn and rearranging gives; m/n = a - n/m. Simply the fractions m/n and n/m such that it is in its most reduced form and the fraction becomes b/c = a - c/b. b and c are coprime or either or both is 1. Rearrange gives b/c = (ba-c)/b and then c(ba-c)=b^2. One case is that b and c are coprime and are both greater than 1 but then b cannot divide c or divide ba-c. So no solutions here. The other case is that either of b and c are 1. If b=1 then c>1. c(ba-c)=1. c is an integer greater than 1 so c*(ba-c) is either 0<, 0 or >1. This does not satisfy the equation. b and c are symmetrical since we could have taken away b/c instead of the c/b earlier. So no solutions here. The other case is that both c and b are 1. But then m=n from earlier. But this is not distinct so no solutions here.