Are you in or are you out?
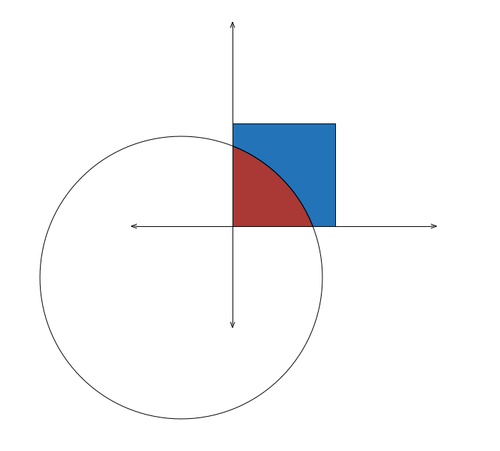 Suppose we have a square
A
B
C
D
with corners
A
(
0
,
0
)
,
B
(
0
,
2
)
,
C
(
2
,
2
)
,
D
(
2
,
0
)
.
Suppose we have a square
A
B
C
D
with corners
A
(
0
,
0
)
,
B
(
0
,
2
)
,
C
(
2
,
2
)
,
D
(
2
,
0
)
.
If a circle with center O ( − 1 , − 1 ) and radius r is such that half of the square's area lies within the circle, what is ⌊ 1 0 0 0 ∗ r ⌋ ?
The answer is 2930.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I used integration instead
( x + 1 ) 2 + ( y + 1 ) 2 = r 2
From
y = 0 to r 2 − 1 − 1
Equated it to 2(half of area of square)
And got this
2 r 2 ( t a n − 1 [ r 2 − 1 ] − t a n − 1 [ r 2 − 1 1 ] ) − r 2 − 1 = 1
Then used wolfy for exact value r = 2.9306....
Log in to reply
Great. Thanks for posting this, Krishna. I actually tried the calculus approach first but "Wolfy" had difficulty solving the equation for some reason, so I resorted to finding a different equation using a non-calculus method.
Log in to reply
But I am still struggling in your previous problem integration is too lengthy in it, finding a new approach to solve it :)
Log in to reply
@Krishna Sharma – I found the integration to be much easier if you move the circle to be centered at (0,0) and the square to (1,1), (1,3), (3,3), (3,1).
Log in to reply
@Andy Hayes – Shifting of origin yeah this one is much easier thanks!
Nice problem as always sir Brian CharlesWorth and that's exactly the Kind of problem I like, I also solved This one using Calculus ^^. P.S: I solved two of your level 5 problems but I'm still at level 4 in Geometry,is it normal? Thanks in advance.
Log in to reply
Thanks, Oussama. I try to create problems that have several different ways of solving them. :)
As for getting from level to level in a topic, I think that it's a matter of answering enough questions at your present level or higher before your level is raised. Say, for example, you are at the middle of level 4, which would give you a rating of about 1875. Answering a level 4 question might give you about 20 rating points, a level 5 question about 40 points. So answering two of my level 5 questions would get you up to a rating of about 1955, but you need to get to a rating of 2000 before your level gets raised to 5. So if you were to answer a few more level 4 or level 5 questions in geometry your level will likely go up.
We used to be able to see our ratings, but now you have to pay for Brilliant 2 to see them, so it's a bit of a guessing game for those of us without. Note that the points indicated next to the title of the question, (in this case 315 points, at the moment), are not the points that would be added to your rating but to your overall point total. In any event, I'm sure you'll get to level 5 soon. :)
Log in to reply
Thanks for your reply, as I tought That the displayed points are the point That are going to be added but it's not the case. Thank You again.
Argh, I got this wrong because I switched arccos to arcsin at the second to last step. #problemswithmessyhandwriting
After days of gazing at the diagram to find another equation to be able to solve for r and θ , I finally ran out of patience today and with guilt used WolframAlpha. After looking at the solution, I am not feeling guilty anymore... :-)

The equation of the circle is ( x + 1 ) 2 + ( y + 1 ) 2 = r 2 . It will then intercept the positive y -axis when
1 + ( y + 1 ) 2 = r 2 ⟹ y = r 2 − 1 − 1 .
(At this point I should mention that this intercept value must be less than 2 , since if it were 2 or greater then, because of the curvature of the circle compared to that of the square's diagonal, the area of the portion of the square within the circle would exceed half the total area of the square.)
By symmetry the circle will intercept the positive x -axis at this value, call it k , as well. Now label points E ( 0 , k ) , F ( k , 0 ) , and let ∠ E O A = θ .
Now as O A = 2 , O E = r and A E = k , we can use the Cosine Law on triangle Δ E O A to find that
k 2 = r 2 + 2 − 2 2 ∗ r cos ( θ ) ⟹ cos ( θ ) = 2 2 ∗ r r 2 + 2 − k 2 = 2 ∗ r 1 + r 2 − 1 ,
where I have substituted for k and simplified.
Now the area of Δ E O A will be 2 k , so by symmetry the combined areas of Δ E O A and Δ F O A will be k . Also, the area of (circular) sector A E F is 2 1 r 2 ∗ 2 θ = r 2 ∗ θ . Thus we are looking for r such that
area(sector A E F - (area( Δ E O A ) + area( Δ F O A )) = 2
⟹ r 2 cos − 1 ( 2 ∗ r 1 + r 2 − 1 ) − ( r 2 − 1 − 1 ) = 2 .
Solving this using numerical methods, (I just used WolframAlpha), we get a value of r = 2 . 9 3 0 6 2 2 2 5 9 . . . . . , making ⌊ 1 0 0 0 ∗ r ⌋ = 2 9 3 0 .
I can't see a way of avoiding using numerical methods at the end, but I think that getting a 'reasonable' equation in r is challenge enough. I preferred this method to a calculus approach, but that method would be quite valid as well.