Are you Perfect or Superperfect?
 How many
Perfect Numbers
are there which are also
Super Perfect
?
How many
Perfect Numbers
are there which are also
Super Perfect
?
Details and Assumptions
is called a superperfect number when
denotes the sum of the divisors of (from to inclusive).
Image Credit: Wikimedia Perfect Number by Deryni
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
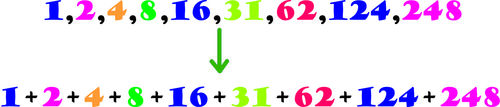
σ ( σ ( n ) ) = 2 n
or, σ ( 2 n ) = 2 n [As n is perfect σ ( n ) = 2 n ]
Always σ ( k ) > k , as the minimum value of σ ( k ) is k + 1 , when k is prime.
σ ( 2 n ) = 2 n so this cannot be true.So there are no perfect number which is superperfect.So the answer is 0