Are you smarter than me? 34

Let me write out the solution as suggested by Incredible Mind.

Let $x = \sqrt{3}\cos {\theta}$ and $y = \sqrt{3}\sin {\theta}$ .

Then, we have:

$f(x,y) = (3x+10y)^2+(8x+11y)^2$

$= (3\sqrt{3}\cos {\theta} + 10\sqrt{3}\sin {\theta})^2 + (8\sqrt{3}\cos {\theta} + 11\sqrt{3}\sin {\theta})^2$

$= 27\cos^2 {\theta} + 180\sin {\theta}\cos {\theta} + 300\sin^2 {\theta} + 192\cos {\theta} + 528\sin {\theta}\cos {\theta} + 363\sin^2 {\theta}$

$= 219\cos^2 {\theta} + 708\sin {\theta}\cos {\theta} + 663\sin^2 {\theta}$

$= 219 + 354\sin {2\theta} + 444\sin^2 {\theta}$

$= 219 + 354\sin {2\theta} - 222(1 - 2\sin^2 {\theta}) + 222$

$= 354\sin {2\theta} - 222\cos {2\theta} + 441$

$\Rightarrow f(x,y) = f(\theta) = 354\sin {2\theta} - 222\cos {2\theta} + 441$

Maximum of $f(\theta)$ occurs when $\frac {d}{d\theta} f(\theta) = 0$ .

$\frac {d}{d\theta} f(\theta) = \frac {d}{d\theta} (354\sin {2\theta} - 222\cos {2\theta} + 441)$

$\quad \quad \quad \quad = 708 \cos {2\theta} + 444 \sin{2\theta}$

$\frac {d}{d\theta} f(\theta) = 0\quad \Rightarrow \tan {2\theta} = - \dfrac {708}{444} = - \dfrac {59} {37}$

$\quad \Rightarrow \sin {2\theta} = \dfrac {59}{ \sqrt {4850} }\quad \Rightarrow \cos {2\theta} = - \dfrac {37}{ \sqrt {4850} }$

Substituting in $f(\theta)$ , we have:

$f(\theta) = 354\sin {2\theta} - 222\cos {2\theta} + 441$

$\quad \quad = 354\times 0.847190627- 222\times (-0.531289037) + 441$

$\quad \quad = \boxed{858.852}$

Lagrange multipliers strike again!

We have a condition of $g(x,y)=x^2+y^2-3=0$ and want to minimize $f(x,y)=73x^2+221y^2+2\cdot118xy$ (note that $221-73=118$ ). This implies there's a number $\lambda$ such that $\vec{\nabla}f=\lambda\vec{\nabla}g$ . Computing the gradients, we get $\vec{\nabla}f=2(73x+118y,221y+118x)$ and $\vec{\nabla}g=2(x,y)$ .

First, we can notice that $x=0 \Leftrightarrow y=0$ and $f(x,y)=0$ . That's a minimum, we don't want that. Otherwise, we can express $\lambda=73+118k=221+118\frac{1}{k}$ ( $k=x/y$ is defined here). That leads to a well-known quadratic equation $k^2-k-1=0$ with solution $x=y\frac{1\pm\sqrt{5}}{2}$ . Using the condition $g(x,y)=0$ gets us $y=\pm\sqrt\frac{6}{5\pm\sqrt{5}}\,, x=\pm\sqrt\frac{6}{5\mp\sqrt{5}}\,.$

Clearly, the maximum is attained for identical signs of $x$ and $y$ . Substituting back into $f(x,y)$ , we get the value in the maximum as (along the way, we pick the right $\pm$ signs) $221\cdot\frac{6}{5\pm\sqrt{5}}+73\cdot\frac{6}{5\mp\sqrt{5}}+2\cdot118\cdot\frac{6}{\sqrt{20}}=221\cdot\frac{6(5\mp\sqrt{5})}{20}+73\cdot\frac{6(5\pm\sqrt{5})}{20}+2\cdot118\cdot\frac{6\sqrt{20}}{20}=\frac{(221+73)\cdot30+(221-73)\cdot6\sqrt{5}+118\cdot24\sqrt{5}}{20}=3(147+59\sqrt{5})\,.$ tl;dr the answer is $3(147+59\sqrt{5})$ . The smart way, of course, would've been to avoid this last long simplification and just throw the values of $x,y$ into a calculator.

EASY, change to parametric form hence x=(3^0.5)cost and y=x=(3^0.5)sint. Now substitute into the required function and you get f(t)=3( (3cost+10sint)^2+(8cost+11sint)^2 ) Just differentiate with respect to t and hence find max/min .You will find t=1.065

${ x }^{ 2 }+{ y }^{ 2 }=3\quad is\quad a\quad circle\quad and\quad { (3x+10y) }^{ 2 }+{ (8x+11y) }^{ 2 }=k\quad is\quad an\quad ellipse.\\ k\quad will\quad be\quad maximum\quad when\quad the\quad ellipse\quad just\quad touches\quad the\quad circle\quad externally.\\ Taking\quad polar\quad co-ordinates\\ x=\sqrt { 3 } cos\theta \\ y=\sqrt { 3 } sin\theta \\ and\quad working\quad same\quad as\quad Incredible\quad mind\quad we\quad get\quad the\quad value\quad of\quad k\quad as\quad 858.852.$

For those who aren't as good at trigonometry, there is also a more algebraic way.

First, I added the new condition $y = ux$ where u is a real constant. Substituting this into $x^2 + y^2 = 3$ gives $x^2 + (ux)^2 = 3 \\ \implies x^2(u^2 + 1) = 3 \\ \implies x^2 = \frac{3}{u^2 + 1}$

Now if we use substitutions on the expression we're trying to find the maximum of, we have the following. $\begin{aligned} (3x + 10y)^2 + (8x + 11y)^2 &= (3x + 10ux)^2 + (8x + 11ux)^2 \\ &= x^2 \big((3+10u)^2 + (8+11u)^2 \big) \\ &= \frac{221u^2 + 236u + 73}{u^2 + 1} \end{aligned}$

I'll call this rational expression $f(u)$ . The maximum of $f(u)$ occurs when $f'(u) = 0$ and so by using the quotient rule, we have $f'(u) = \frac{4(-59u^2 + 74u + 59)}{(u^2 + 1)^2}$ For $f'(u) = 0$ , we must have $u$ satisfying $-59u^2 + 74u + 59 = 0$ . From then on it's just a simple use of the quadratic equation and substituting the positive value of $u$ (as that is the value which gives $f(u)$ its maximum) and that gives $(3x + 10y)^2 + (8x + 11y)^2$ its maximum of around 858.852.

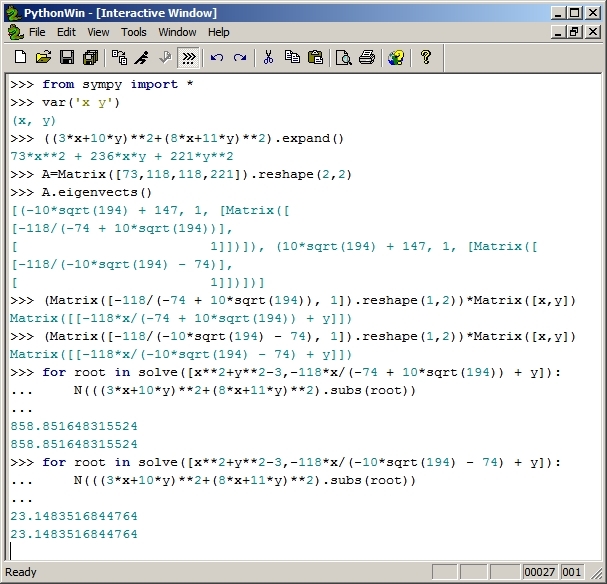
Alternatively, you can perform this calculation using the eigenvectors of the given form. Expand it, express it in simplest terms as a family of ellipses that are not aligned with the co-ordinate axes. Write the ellipses in matrix form and calculate the eigenvectors of this matrix. Express the eigenvectors in co-ordinate form and calculate the intersections of these vectors with the given circle. Now calculate the values of the original ellipse at these intersections. Choose the biggest value. Done here using symbolic algebra. Otherwise I would never have completed this.

Just put x=sqrt(3) cos(m) and y=sqrt(3) sin(m).