Area after rotation
A unit square is rotated 4 5 ∘ counterclockwise about one of its vertices, A .
What is the green area?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
14 solutions
Andrew, I solved it much the same way you did. But when I saw dad's answer I was reminded that he's been a nerd for much longer than we have.
Dammit.
Log in to reply
I have sons and will have to show them this conversation because they will say the same.
What's so inelegant about it? I think it's a pretty nice way of solving.
Log in to reply
The inelegant solution he's referring to is the one from Andrew Gradman, currently 2 posts down.
I saw it as a half plus a 5th, myself, but I've forgotten all the fancy stuff from school. If you continue the bisect through to the top left, the small green triangle fits in the white area 4 times, I believe...so I was looking for a half plus a 5th :/
Log in to reply
That's how I thought of it: "a bit more than half" just by visual intuition. For some of these problems, it's not clear which skillset they want to exercise so I just go with "Test Taking 202" skills :P
How is it inelegant? It is perfect, and is just how I thought about it
Log in to reply
The inelegant solution he's referring to is the one from Andrew Gradman, currently 2 posts down.
Can someone provide the algebra for this solution?
This is exactly how I saw it. Glad to know I'm not alone.
I object to the problem. The author put no scale of length on the diagram. I took a wild guess at the answer and was wrong. Wayne, your son did good work. CAB
Wayne, I guess we’ve been nerds for the same length of time.
Nothing that is correct can ever be inelegant. Not ever.
1/2+1/16=9/16 Quite simple. No Pitagoras.
My thoughts were that the space occupied by the white box is less than half of the total box area, the only answer that fits the requirement is D) 2 - sqrt(2) (assuming the box sides are equal to 1)
how can you say that it will touch the corner???
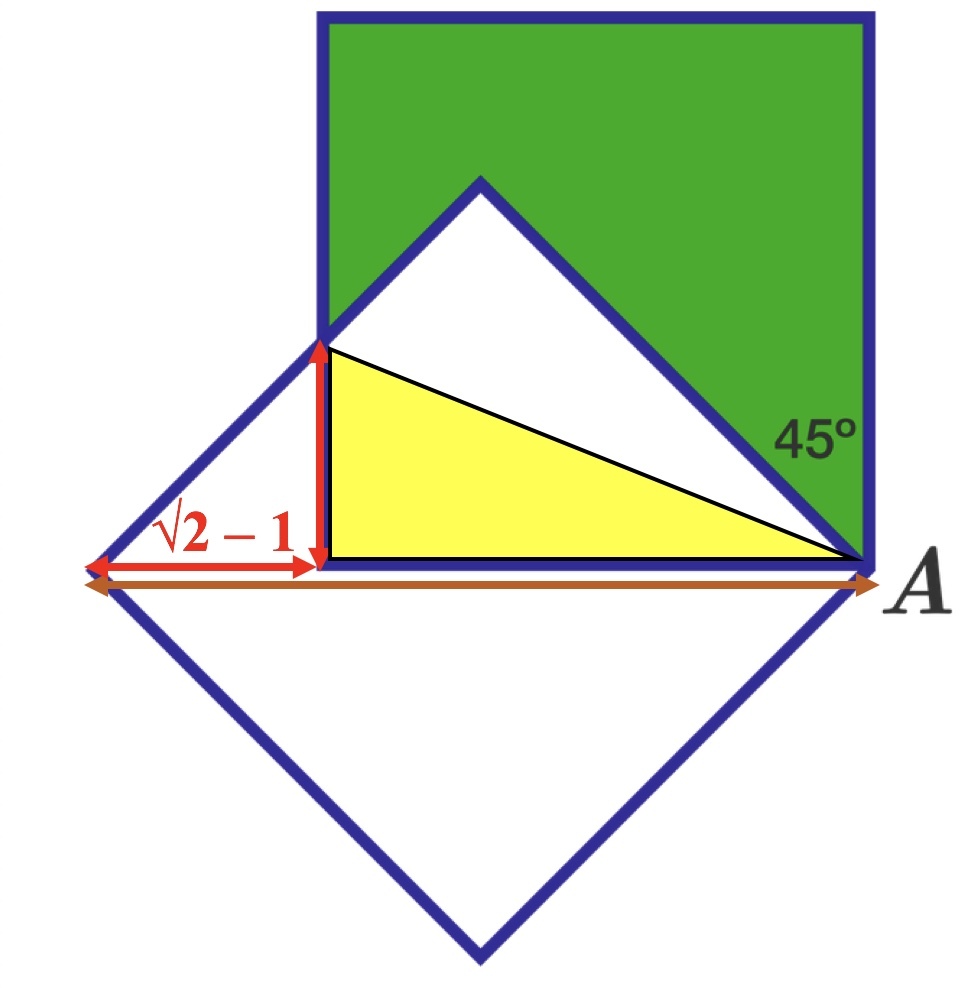
red = brown − blue = 2 − 1 . yellow = 2 1 ⋅ blue ⋅ red = 2 1 ( 2 − 1 ) . green = unit square − 2 ⋅ yellow = 1 − ( 2 − 1 ) = 2 − 2 .
Brilliant. The most elegant solution!
For anyone who needs the algebra... There are twin triangles (yellow and white), with base length 1, so the area of both together is:
(2)½bh = bh = (1)h = √2–1
Subtract this from the area of the unit square (which is just 1), and you’re done!
1–h = 1–(√2–1) = 2–√2
The elegance of this solution comes from choosing a pair of triangles with unit side length to simplify the area calculation of the kite (which area is just the height of one triangle—no further calculations necessary!).
Log in to reply
Yes absolutely! I started calculating the area of the kite and hence found its diagonals and found its area and then substracted from one to get the answer.....but the process was way more complicated as I ended up with too many surds to multiply and substract. But this method is absolutely perfect and is an awesome shortcut.
There is underlying reflection argument that is used here implicitly.
Log in to reply
That is correct. The situation is obviously symmetric.
Log in to reply
It is obvious but not completely trivial. It depends on factorization of rotation into composition of two reflections in a plane. In this particular case, we can choose one reflection to be with respect to diagonal of the square (which leaves the square invariant) so the final shape must have reflection symmetry.
Log in to reply
@Denis Husadzic – There are two squares. They have one vertex in common.
Then square (I) is rotated clockwise relative to square (II) over the same angle as square (II) is rotated counterclockwise relative to square (I).
Thus, exchanging squares (I) and (II) is identical to a rotation-reflection of the plane. This proves that all corresponding dimensions of the squares are congruent and in particular that the overlap is a kite.
Log in to reply
@Arjen Vreugdenhil – Consider a triangle with no two congruent sides and rotate it. The final shape has no reflection symmetry. This is because the starting triangle has no reflection symmetry with respect to line passing through center of rotation, however you choose center of rotation or angle of rotation. I don't follow your argument.
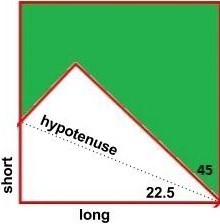
The line of symmetry cuts the kite into a pair of right triangles with angles of 22.5, 67.5, and 90 degrees.
By definition, this triangle has a short:long:hypotenuse ratio of 1 : 1+√2 : √(4+2√2).
Since this is a unit square,
- the "short" length = 1 + √ 2 1
- the white area = 1 + √ 2 1
- the green area = 1 - 1 + √ 2 1
- the green area can also be written as 2-√2 (i.e. multiply numerator and denominator by 1-√2)
- Solve p 2 − p = 2 − √ 2
p 2 = 2
I solved it like your dad, and as I said to your brother, I had to laugh at the family interactions because we would have similar ones. However, I was thinking about generalizing the question for any rotation between 0° and 90° and think your method could be made into a formula.
Rather than bothering to actually solve the problem, we can use logic to eliminate answer choices. 2 1 is clearly not correct (just look at the diagram...). Right triangles with a 45 degree angle have the hypotenuse as 2 times each leg, so 2 must be involved in the answer, and there is no way 3 can be part of the answer. Therefore, 2 − 2 is the only sensible answer.
Hahaha, genius answer!
You aced your SAT math, right? :-)
We think alike, friend, I used exactly this logic!
With 45 degrees, anything root-three is out (30 or 60 degrees would be another story). If the side of the rotated square extended to the opposite corner, the shaded region would be 1/2; it doesn't, so that answer is also out. So three out of four answers are eliminated.
I know this explanation doesn't prove anything, but it is a good multiple choice testing strategy.
Exactly how I did it!
Totally legit way of answering multiple choice!
(Nice to be able to crunch the numbers, too, if you want to double check your answer.)
Divide into two smaller problems: The large green triangle which consists of half the area of the entire square: 1^2/2 The small triangle whose sides are: Sqrt(2)-1 --> area=(sqrt(2)-1)^2/2 Add these areas to get: 1/2 + (sqrt(2))^2/2 -2*sqrt(2)/2 + 1/2 = 1/2 + 1/2 + 1 - sqrt(2) = 2 - sqrt(2)
How did you add 1/2 at the end of the number sentence when adding the areas?
 A
=
2
x
2
−
2
1
2
+
1
2
=
2
(
2
−
1
)
2
+
2
1
=
2
2
−
2
2
+
1
+
1
=
2
4
−
2
2
=
2
−
2
A
=
2
x
2
−
2
1
2
+
1
2
=
2
(
2
−
1
)
2
+
2
1
=
2
2
−
2
2
+
1
+
1
=
2
4
−
2
2
=
2
−
2
We can use the fact that the shape has reflection symmetry with respect to line through points
A
and
E
to get:
 From here we get the following:
1
+
x
=
2
,
A
yellow
+
A
green
=
1
,
A
yellow
=
x
,
and this gives us
A
green
=
1
−
x
=
1
−
(
2
−
1
)
=
2
−
2
.
From here we get the following:
1
+
x
=
2
,
A
yellow
+
A
green
=
1
,
A
yellow
=
x
,
and this gives us
A
green
=
1
−
x
=
1
−
(
2
−
1
)
=
2
−
2
.
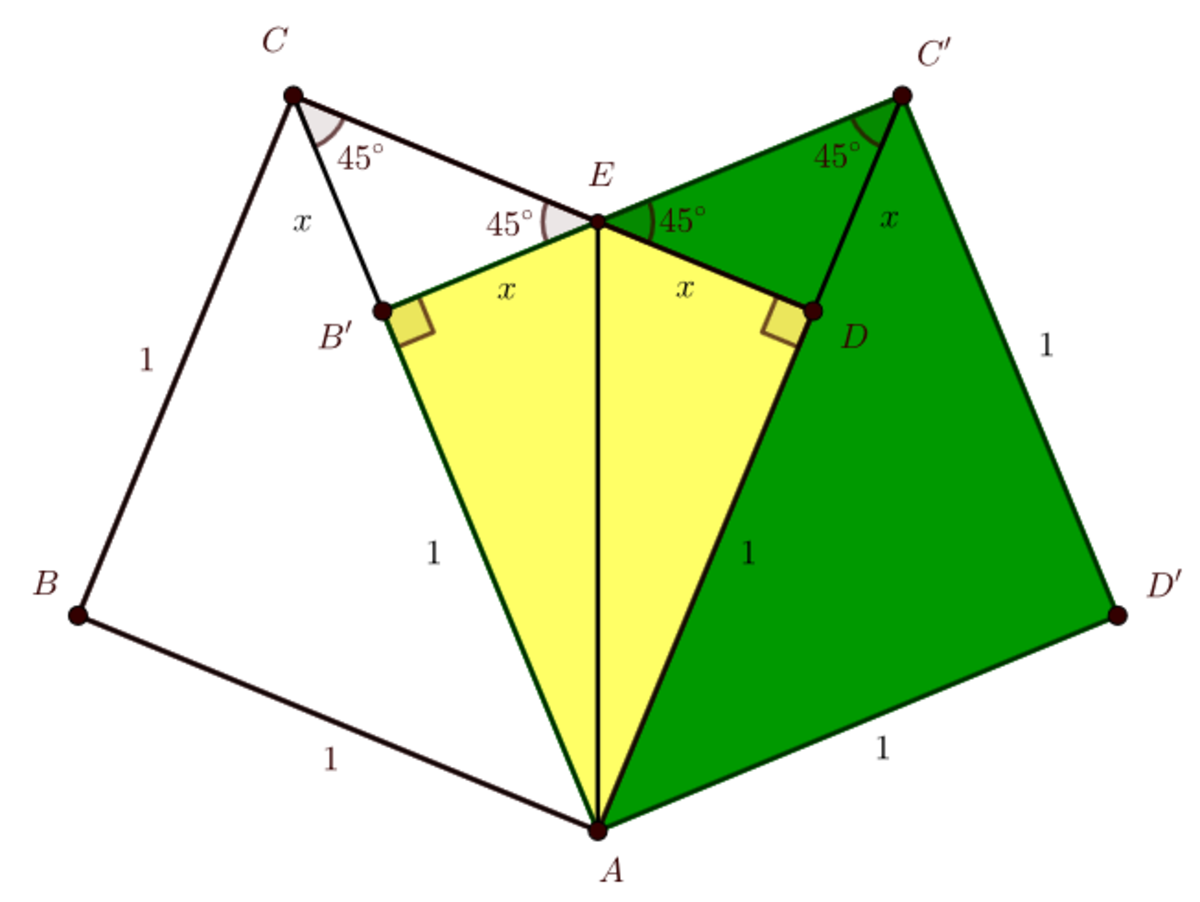
The reflection argument. Any rotation is composition of two reflections. To get rotation by α centered at A choose any two lines through A with angle between them α / 2 . Composition of reflections with respect to those lines gives rotation by α . Switching the order of applying the reflections switches between clockwise and anticlockwise rotation.
In our example, instead of rotating square A B C D by 4 5 ∘ clockwise, we can first reflect it with respect to line A C followed by reflection with respect to line A E . Since square A B C D is invariant under reflection with respect to line A C , we can get square A B ′ C ′ D ′ just by reflecting it with respect to line A E (up to relabeling of vertices).
I deduced a general formula for the green area A of a square of longitude L and which has been rotated an angle of θ (where 0 º ≤ θ < 9 0 º ) by doing the difference of the total area and the intersection area between both squares, which can be divided in a rectangle triangle and a trapezium.
I’m not going to write here the steps of the demonstration, but applying the previous idea and simplifying the expression it’s not complicated to obtain it. This general formula is: A = L 2 ( 1 − cos ( θ ) 1 − sin ( θ ) ) In this particular case, with L = 1 and θ = 4 5 º , the green area is: A = 1 2 ( 1 − cos ( 4 5 º ) 1 − sin ( 4 5 º ) ) = 1 − 2 2 1 − 2 2 = 2 − 2
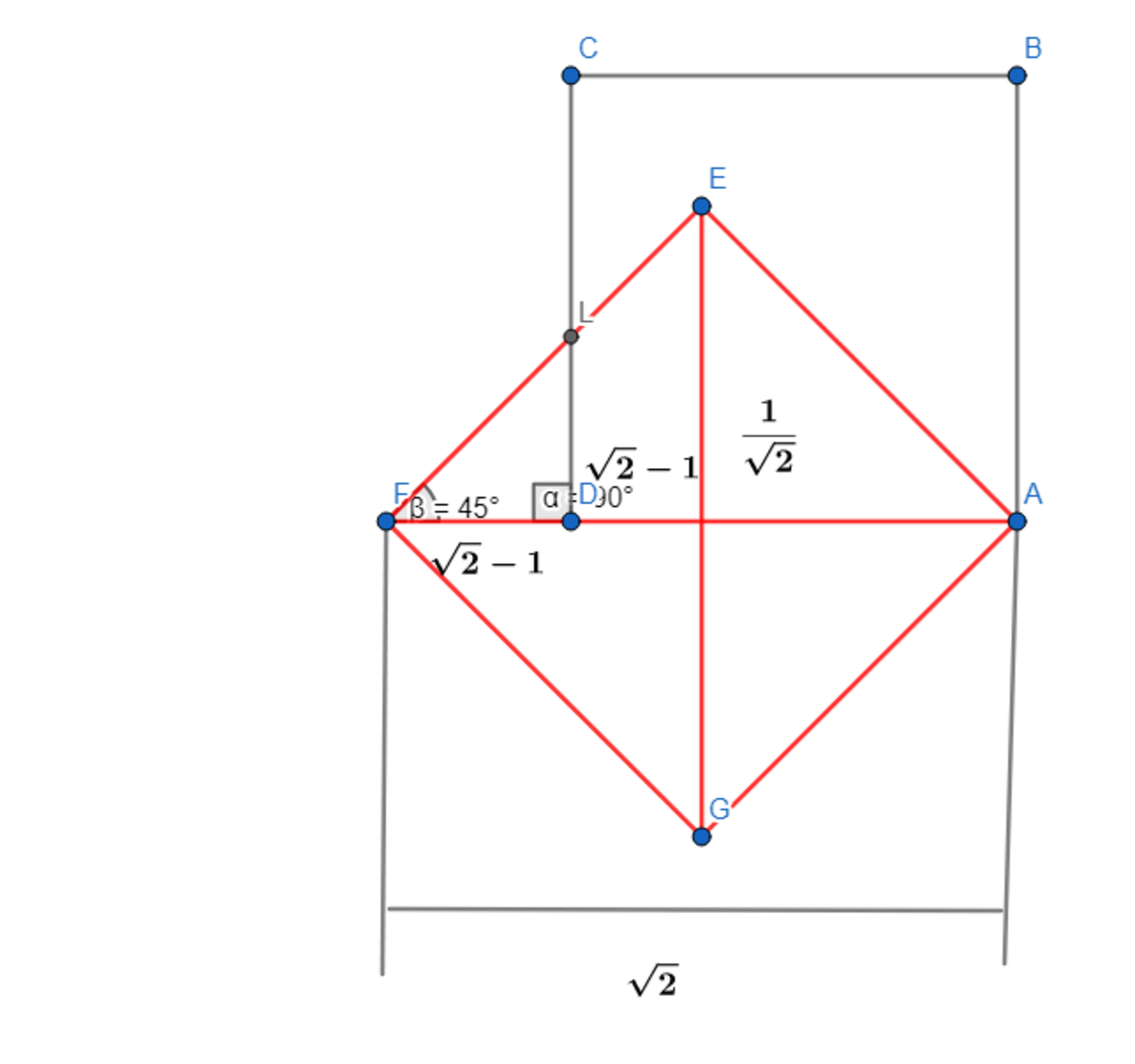
A △ A E F = 2 1
A △ F L D = 2 1 ( 2 − 1 ) 2
A A E L D = A △ A E F − A △ F L D = 2 − 1
∴ The desired green area above is A = 1 − A A E L D = 2 − 2 .
Well if you don't want to mess with calculation just eliminate the options
Clearly area is bigger than 0.5
Next we see that the area is kind of unsymmetrical,so it will not be a/b form
Also ( root 3 )deals with 30 and 60 degrees so we get our answer
Yes I know that's not at all a solution
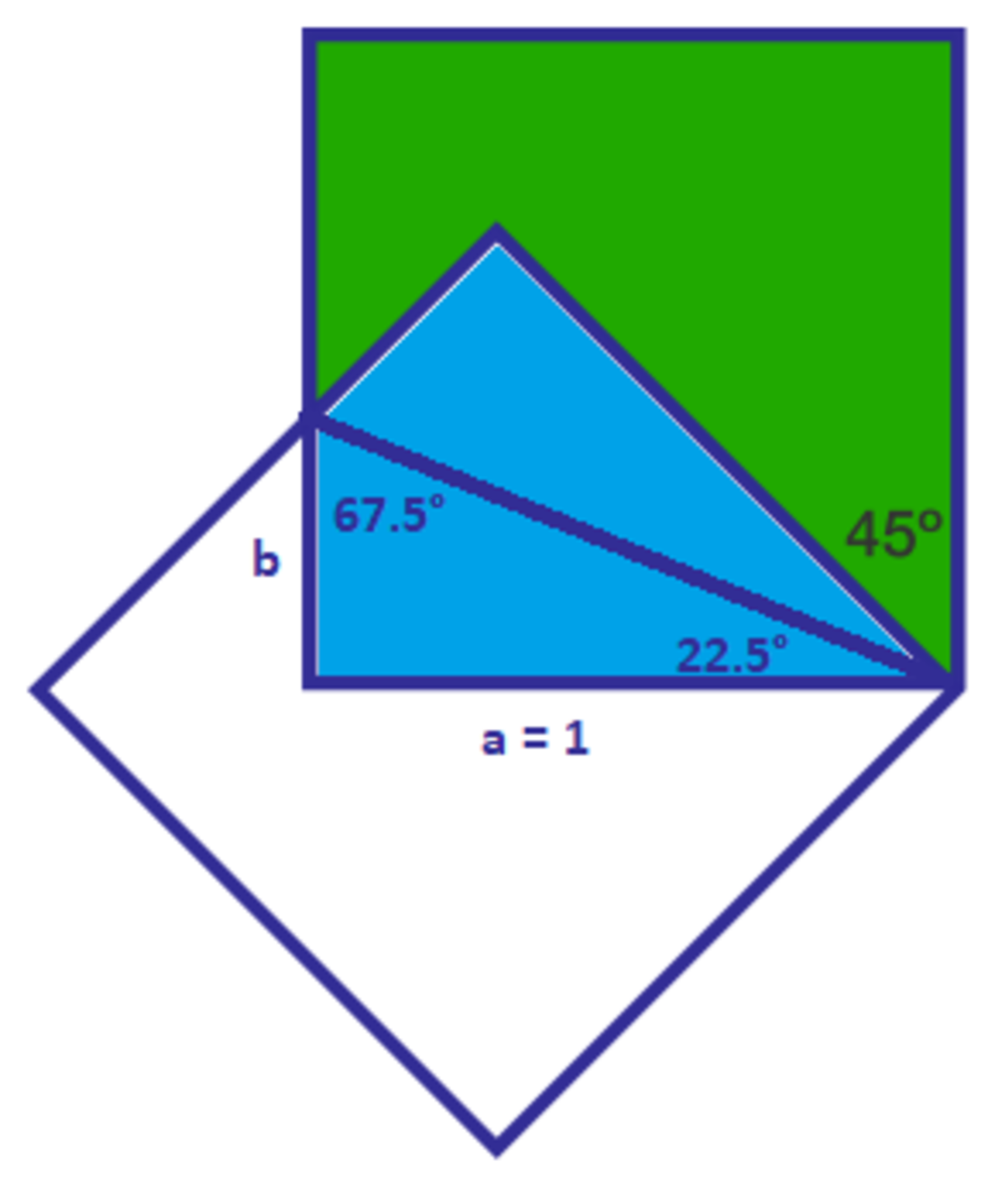
tan(67.5°) = a / b = 1 / b
2.4142 ≈ 1 / b
b ≈ 0.4142
The area of one blue triangle: 1 * 0.4142 / 2
The are of 2 blue triangles: 0.4142
The green area: 1 - 0.4142 ≈ 0.5858 ≈ 2 − 2
If instead of 45° the square were to be rotated counterclockwise about A by a general angle θ (0<θ<90°) we can show that the resulting green area = tan(θ) - sec(θ) + 1 = 2 -√2 at θ = 45°.
I’d be really interested to see the derivation of that formula.
Log in to reply
Refer to the diagram by Gergely Gyetvai above. You can easily see that the area of the "blue" kite is = 2 [1 x tan(45°- θ/2)/2 ] = tan(45°- θ/2) Hence green area = 1 - tan(45°- θ/2). Now, tan(45°- θ/2) = (1-tan(θ/2)/(1+tan(θ/2)) = [cos(θ/2) -sin(θ/2)]/ [cos(θ/2) +sin(θ/2)] = [cos(θ/2) -sin(θ/2)]²/ [cos²(θ/2) -sin²(θ/2)] = [1 -2sin(θ/2) cos(θ/2)]/[cos(θ)] = [1 - sin(θ)]/cos((θ) = sec(θ) - tan(θ) or 1 - tan(45°-θ/2) = 1 - [sec(θ) - tan(θ)] =1 + tan(θ) - sec(θ)
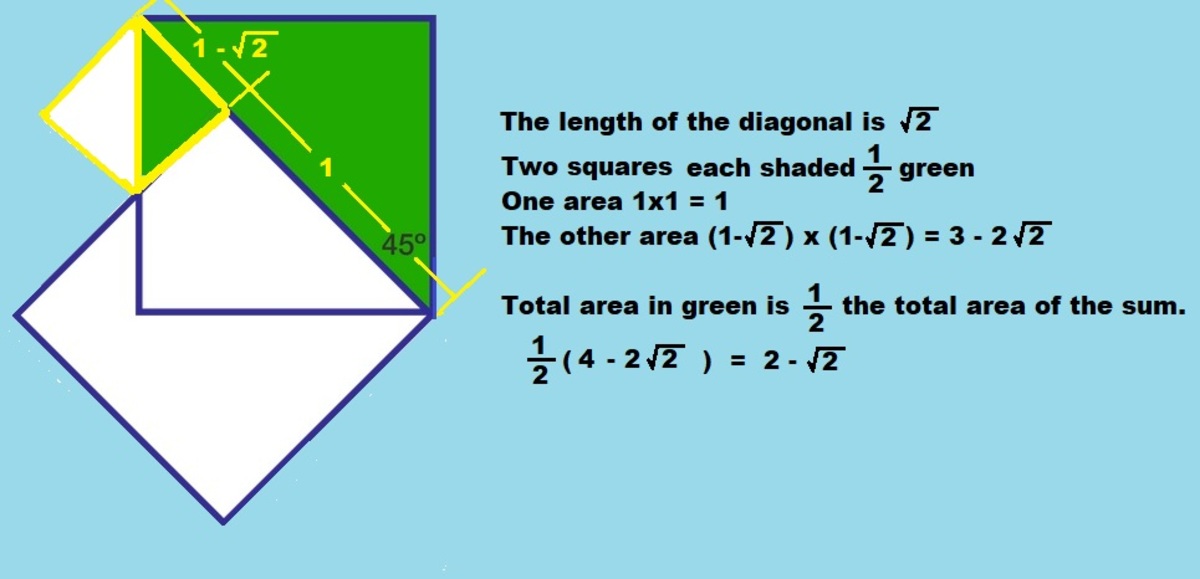
My son's proposed solution is correct, but inelegant.
The green area consists of a large right isosceles triangle (short edges of length = 1), and a small right isosceles triangle (short edges of length = √2-1).
Thus, the green area = 2 -√2, and p^2=2.