Area Of Overlapping Leaves
The side of the square is a . Express the green area with a .
Each square's vertex is a circumcentre of appropriate circular arc.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
A nice approach. I did like it for its being out of box. I have up voted your solution. You can make your calculations easy and short. You may see my calculations.
Log in to reply
I just saw your solution. It is.... much less text :)
Thank you for the upvote and the praise. I guess that I always tend to do things with unnecessary complications. Thanks for sharing your solution with the community.
One more way.. If we calculate the area of the floral shape with the middle part coming in it twice and then substract the area of the same shape in which the area of the middle part is taken only once from it we get the required result. It is an easy way to solve the problem. Yours method is also good.
Log in to reply
Can you please write how you can use your method here! Thanks.
I still don't understand how you know |BQ| equals a. I mean, the equation you used to draw the curves makes |BQ| = a. But I don't have that equation, and I don't have any variable to figure that out or express the result with it. I could have made the flower more wide open (being the entire area of the flower very close to a²), or more closed, having an area very close to 0. Unless I'm supposed to use a rule to measure |BQ| and |AB| and notice they are the same here, I'm still not sure how you would know. What am I missing?
Log in to reply
Notice that arc AMQC is drawn with centre B, and radius a.
Log in to reply
But that way you are assuming the curve AMQC is an arc of a circumference centered at B. How can you be sure it is, when the question said nothing about it? I can draw a curve that touches A and C and is not an arc of a circle. Or can't I?
Log in to reply
@Rafael Perrella – You have a point. It is obvious to some extent, I believe. Many people have solved the problem correctly, which means they made the right assumption. Anyhow, I (will) have added those crucial pieces of information, to this and other problems :3
Log in to reply
@Milan Milanic – Thanks! When I read a geometry problem (which I'm not very good at), I always try to think about what variables I'd need for it to be solvable first, then I can try to develop my own ideas to solve it (like I said, I'm not very good at it, so I know almost no properties or formulas, except for the simplest ones everyone learns). This problem felt incomplete to me, with multiple answers, so I couldn't solve it. But I understand the question and data provided was very obvious to someone who is used to geometry and problems like this.
@Rafael Perrella – The problem states, """ Each square's vertex is a circumcentre of appropriate circular arc.""" I hope you are satisfied.
Log in to reply
@Niranjan Khanderia – @Niranjan Khanderia I have added that recently. So Rafael is not to blame on this. :)
How did you calculate QN? Can you please elaborate? @Milan Milanic
Log in to reply
I will be using the modified picture used for explaining my solution. Let's add 2 more points to that image, point G and K , which are the midpoints of segments A B and C D , respectively.
As the solution states, it is noted that △ A B Q is equilateral, whose sides are a in length. Therefore, the altitude of such triangle (corresponding with segment G Q ), is 2 a 3 . It is obvious that segment G K is a in length, thus Q K 's length must be the subtraction of G K 's length with G Q 's, that is a − 2 a 3 = a ( 1 − 2 3 ) . The same logic goes with length of segment G N .
In the end ∣ Q N ∣ = ∣ G K ∣ − ∣ G N ∣ − ∣ Q K ∣ = a − 2 × a ( 1 − 2 3 ) = a ( − 1 + 3 ) .
I hope this was somewhat helpful. If not, hit me up once more.
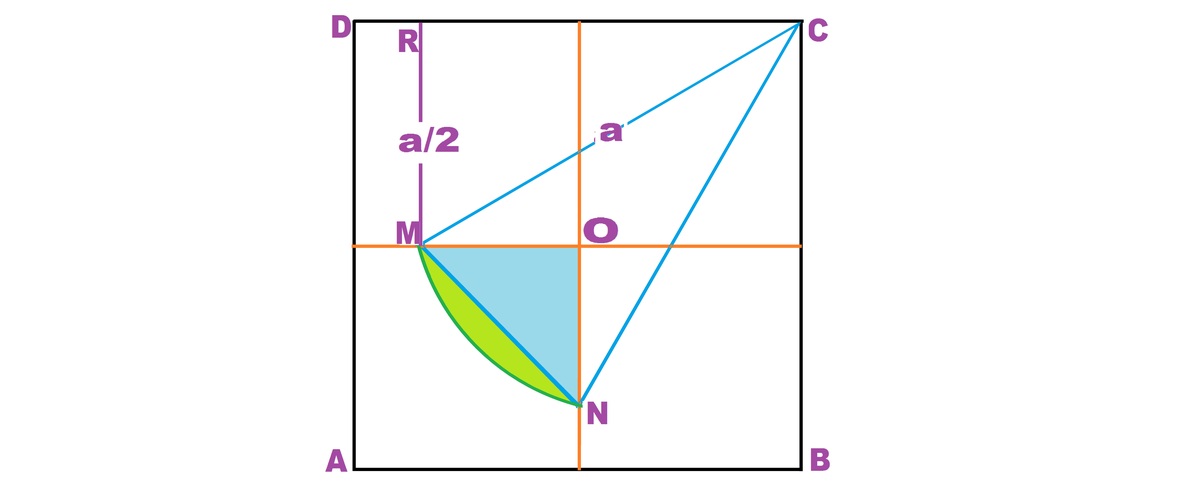 ABCD is a square with sides a. O is the center. It is divided ito 4 equal squares.
A quarter of the flower is shown as area OMN.
L
e
t
M
R
⊥
C
D
.
I
n
r
t
.
Δ
M
C
R
,
2
R
M
=
H
y
p
.
M
C
.
⟹
∠
M
C
R
=
3
0
o
∵
o
f
s
y
m
m
e
t
r
y
,
∠
B
C
N
=
3
0
o
.
C
l
e
a
r
l
y
∠
N
C
M
=
3
0
o
.
∴
Δ
M
N
C
i
s
a
−
3
0
o
−
a
.
C
R
=
2
3
a
,
∴
M
O
=
2
3
a
−
2
1
a
.
R
e
q
u
i
r
e
d
a
r
e
a
=
4
∗
{
a
r
e
a
C
M
N
}
=
4
∗
{
a
r
e
a
o
f
s
e
c
t
o
r
N
C
M
−
(
a
r
e
a
s
o
f
Δ
s
M
O
C
a
n
d
N
O
C
)
}
=
4
∗
{
π
∗
a
2
∗
3
6
0
o
3
0
o
−
2
∗
2
1
∗
M
O
∗
2
a
=
3
a
2
(
π
+
3
−
3
3
.
)
ABCD is a square with sides a. O is the center. It is divided ito 4 equal squares.
A quarter of the flower is shown as area OMN.
L
e
t
M
R
⊥
C
D
.
I
n
r
t
.
Δ
M
C
R
,
2
R
M
=
H
y
p
.
M
C
.
⟹
∠
M
C
R
=
3
0
o
∵
o
f
s
y
m
m
e
t
r
y
,
∠
B
C
N
=
3
0
o
.
C
l
e
a
r
l
y
∠
N
C
M
=
3
0
o
.
∴
Δ
M
N
C
i
s
a
−
3
0
o
−
a
.
C
R
=
2
3
a
,
∴
M
O
=
2
3
a
−
2
1
a
.
R
e
q
u
i
r
e
d
a
r
e
a
=
4
∗
{
a
r
e
a
C
M
N
}
=
4
∗
{
a
r
e
a
o
f
s
e
c
t
o
r
N
C
M
−
(
a
r
e
a
s
o
f
Δ
s
M
O
C
a
n
d
N
O
C
)
}
=
4
∗
{
π
∗
a
2
∗
3
6
0
o
3
0
o
−
2
∗
2
1
∗
M
O
∗
2
a
=
3
a
2
(
π
+
3
−
3
3
.
)
First, let the area of the square is A = a 2
Picture 1 .
The blue area is a quilateral with side lenght a . Let the area of the blue area is x , then
x = 2 1 × a 2 × sin 6 0 ∘ = 4 a 2 3
The yellow area is a sector of a circle with radius a and an angel 3 0 ∘ . Let the area of the yellow area is y , then
y = 3 6 0 ∘ 3 0 ∘ × π a 2 = 1 2 π a 2
So, we have the area of the white area-let the area of the white area is z - namely:
z = A − x − 2 y = 1 2 a 2 ( 1 2 − 3 3 − 2 π )
Picture 2 .
Let the area of the gray shaded area is u , then
u = A − 3 6 0 ∘ 9 0 ∘ × π a 2 − 2 z = 1 2 a 2 ( − 1 2 + 6 3 + π )
Picture 3 .
Thus, the area of the green area is
A − 4 z − 4 u = 3 a 2 ( π + 3 − 3 3 ) □
I like your solution!
Log in to reply
Excellent way!!! I used the Cos of Pi/6 to help to solve it...
Solution:
I will divide this problem in two parts. First one, find the gray area, second one, find the yellow area. Gray area + yellow area is the solution.
Gray area:
Let's concentrate on point Q (or: M , N or P , conclusion will be the same). I believe, that it can be spotted that B Q and A Q 's length is a . Therefore, triangle A B Q is equilateral. Height of that triangle is 2 a 3 . Since the distance between point Q and segment C D is as same as the distance between point N and segment A B , we can calculate that Q N = a ( 3 − 1 ) . Q N = M P and using Pythagoras's theorem we get that the lenght of □ M N P Q 's side is a 2 − 3 . Therefore, the smaller square's area is a 2 ( 2 − 3 ) .
Yellow area:
∠ N C M = 3 0 ° , which is 1 2 3 6 0 ° , so the area of circular sector is 1 2 a 2 π . If we find the area of triangle N C M then we only need to subtract its area from the area of sector N C M and that will give us 1st part of yellow area. We will use Pythagoras's theoreme once more to find the height of triangle N C M . Height 2 = M C 2 − ( 2 M N ) 2 and H e i g h t = 2 a 2 + 3 . So, triangle's area is 2 N M × H e i g h t = 4 a 2 . Then, the 4 1 of the yellow area is 1 2 a 2 ( π − 3 ) . It is obvious, that the yellow area is 3 a 2 ( π − 3 ) .
Conclusion: Gray area + yellow area => a 2 ( 2 − 3 ) + 3 a 2 ( π − 3 ) = 3 a 2 ( π + 3 − 3 3 )