Area from a Perpendicular Sum
A B C D is a convex cyclic quadrilateral such that A B = A D and ∠ B A D = 9 0 ∘ . E is the foot of the perpendicular from A to B C , and F is the foot of the perpendicular from A to D C . If A E + A F = 1 6 , what is the area of A B C D ?
The answer is 64.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
We know that ABE and AFD are similar because <EAF = <BAD = 90 degrees. AB = AD, so AEB is congruent to AFD (and AE = AF). Thus the area of ABCD is the area of AECF. Then [AECF] = AE AF = (16/2) (16/2) = 64.
Let's take a closer look at A E C F . We have ∠ E C F = ∠ B C D = 1 8 0 ∘ − ∠ B A D = 9 0 ∘ . Hence, A E C F is a rectangle and ∠ E A F = 9 0 ∘ , which gives ∠ B A E = ∠ D A F . Thus A E = A B cos ∠ B A E = A D cos ∠ F A D = A F , hence it is a square.
Furthermore, A B E is congruent to A F D , so [ A B C D ] = [ A E C F ] = 8 2 = 6 4 .
For this problem we know that A B = A D and that ∡ B A D = 9 0 ° .
We also know that the feet E and A lie on the lines BC and DC.
Since this is the case we can deduce the following.
∡ A B C ≤ 9 0 °
∡ A D C ≤ 9 0 °
Since this is a cyclical quadrilateral, the angles ABC and ADC cannot both be less than 90 degrees therefore they must equal 90 degrees and the cyclical quadrilateral we're dealing with is simply a square.
This means that foot E lies at point B and foot F lies at D.
Therefore
A B = A D = A E = A F
Since A B = A D and A E + A F = 1 6 , A B and A D are equal to 8.
Thus the area is simply A = s 2 which is 64.
Note that ABCD need not be a square. The feet lies on the lines, and not on the line segments, hence it need not be true that ∠ A B C ≤ 9 0 ∘ .
Log in to reply
I'm kind of confused since AB=AD. If the line segments coming from one point are equal, how can it be any rectangle and not specifically a square? What's going on here?
Log in to reply
Here is a crude image of a possible setup, where ABCD is not a square. All we have is that B A D is a right isosceles triangle, and that B C D is a right triangle. We do not yet know that B C D is a right isosceles triangle (and in fact it need not be.
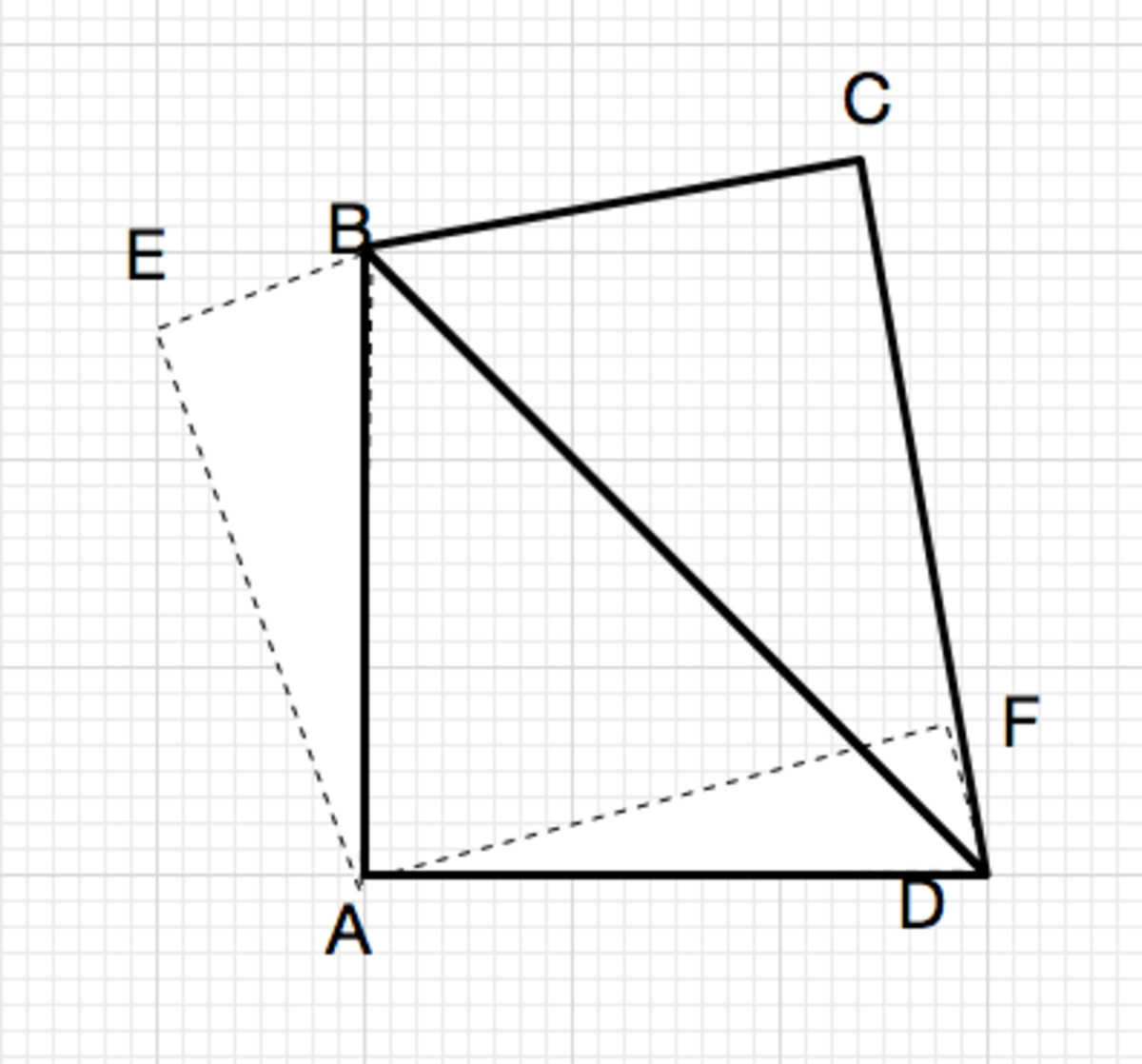
Log in to reply
@Calvin Lin – Two problems I see in this image:
-
ABCD should be a cyclic quadrilateral - meaning all vertices all lie on a single circle.
-
EB is not part of BC so how come AE passes as a perpendicular from A to BC?
Please help me understand if I missed something.
Log in to reply
- What makes you think that ABCD isn't a cyclic quadrilateral here? As long as BAD and BCD are right angles, we have a cyclic quadrilateral. There are more cyclic quadrilaterals than just squares and rectangles.
- The perpendicular to a line doesn't need to intersect a particular line. E.g. in an obtuse triangle, there will be a perpendicular that doesn't intersect the base.
Ptolemy's theorem expresses the product of the lengths of the two diagonals p and q of a cyclic quadrilateral as equal to the sum of the products of opposite sides:
pq = ac + bd.
also here both diaginals are equal to the diameter as it has angle A=90 and angle inscribed in a semicircle is 90
so by ptolemy thm ac+bd=ad+bc ..1
now let AB(a)=AD(c)=x then BD=p^2=2x then from 1 a=d similarly we can say a=b=c=d=x also one angle 90 hence a square sum of 2 sides=16 each side=8 hence area =64
Since ABCD is a cyclic quadrilateral, ∠BAD + ∠BCD = 180∘ And, since ∠BAD is 90∘, ∠BCD is also 90∘. Therefore, to make ABCD a cyclic quadrilateral with 2 opposite angles, equalling to 90∘ each, the other 2 angles also have to be 90∘ and has to be a square. Since E and F are foots of perpendicular from A to BC and A to DC respectively, E is actually B, F is actually D. Hence, AE + AF = AC + AD = 16. As ABCD is a square, AB = AC = 8. To find the area of square, it would be length x length = 8 x 8 = 64
Given \angle BAD = 90 ^ \circ In a cyclic quadrilateral opp. angles are complementary. Thus, \angle BCD=90^ \circ. Given AB=AD. In the quadrilateral, two adjacent sides are equal and opp. angles are 90^ \circ. Thus, it is a square. Then, AE+AF=16 gives sum of its sides. Therefore, side of the square=8. Area=64
As ABCD is a cyclic quadrilateral, by the property that opposite angles are supplementary, ∠BCD = 90° the perpendicular to either of DC and CB will be in the exterior of the quadrilateral. We can see it by observation. Now after drawing the perpendiculars to AE and AF, we get a quadrilateral AFCE in which ∠AEC =∠ECF = ∠AFC = 90° . So by angle sum property of a quadrilateral, ∠FAE = 90° . So this quadrilateral turns out to be a parallelogram. [since the angles are right, it is a rectangle - Calvin]
We can also see that ΔAEB and ΔAFD are formed. We can show that these two Δs are similar by the Angle-Side-Angle congruency criterion. This implies that the perpendiculars AE and AF are also congruent. It means each of them is 8 and the quadrilateral AFCE is a square with area = 64. Now [ABCD]=[AFCE]-[AFD]+[AEB] . But since AEF and AEB are congruent, we get [ABCD]=[AFCE] Therefore, [ABCD]= 64