Area of a Rectangle
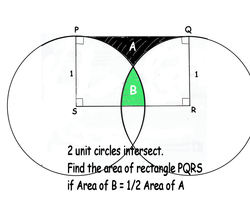 Find the area of the rectangle correct to 3 decimal places.
Find the area of the rectangle correct to 3 decimal places.
Hint: The length of SR varies from 2 to 0. At 2, B = 0 and A is maximum, thus B/A = 0. As SR decreases from 2 to 0, B increases and A decreases and B/A increases. You're to find SR and thereby the area of PQRS when B/A = 1/2
The answer is 1.686.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I got eq.1 but couldn't solve it . Can you pease tell me how to solve such equations involving both angkes and their trigonometric ratios.
Nicely done, Adit. There is one typo in the second line of math; it should be (sin<XSR)(cos<XSR)/2.
Also, the equation simplifies to
cos ( Y ) ( 2 + sin ( Y ) ) − Y = 2 π ,
where Y is in radians. The one positive solution to this equation is 0 . 5 6 8 3 8 5 8 4 . . . . . , as found here .
The desired solution, as you have noted, is then
2 cos ( Y ) = 1 . 6 8 5 5 4 1 8 5 . . . . . . .
It still required WolframAlpha, etc., to find the solution, but at least you established the necessary equation without resorting to calculus. I'm impressed. :)
Let S be the origin and S R = a lie on the positive x -axis. Since the height of rectangle P Q R S is 1 its area will then just be a .
The circle on the left then has equation x 2 + y 2 = 1 and the circle on the right has equation ( x − a ) 2 + y 2 = 1 . The uppermost point of intersection of the two circles lies at ( 2 a , 1 − ( 2 a ) 2 ) .
The area of region A will then be
2 ∗ ∫ 0 2 a ( 1 − 1 − x 2 ) d x ,
and the area of region B will be
2 ∗ ∫ 2 a 1 1 − x 2 d x .
So for the area of B to be one-half the area of A we must have
2 ∗ ∫ 2 a 1 1 − x 2 d x = ∫ 0 2 a ( 1 − 1 − x 2 ) d x
⟹ sin − 1 ( 1 ) − sin − 1 ( 2 a ) − ( 2 a ) 1 − 4 a 2 = 2 a − ( 2 1 ) sin − 1 ( 2 a ) − ( 4 a ) 1 − 4 a 2
⟹ a + sin − 1 ( 2 a ) + ( 2 a ) 1 − 4 a 2 = π .
At this point I resorted to an application of WolframAlpha, which gave a solution of a = 1 . 6 8 6 to 3 decimal places.
Note that in general, if the area of region A is n times that of region B , (where n ≥ 0 is a real number), then the area a of rectangle P Q R S is the solution to the equation
a + ( n − 1 ) arcsin ( 2 a ) + ( n − 1 ) ( 2 a ) 1 − 4 a 2 = 2 n π .
Note that ∫ 1 − x 2 d x = ( 2 1 ) ( sin − 1 ( x ) + x 1 − x 2 ) + C .
So this means that this problem can't be solved with basic geometry. Is it??
Log in to reply
I'm not sure. I'm still looking for a basic geometry solution, but I'm starting to lose hope that there is one.
Log in to reply
Not just that, I don't think there is an algebraic solution. The value of 1.686 doesn't seem to nicely relate to anything.
Log in to reply
@Calvin Lin – I think I have a trigonometric solution, but you must use a calculator or wolfram alpha on the final step
Log in to reply
@Trevor Arashiro – Great! I used WA on my final step anyway, so that's not a big deal. So what is your method?
Log in to reply
@Brian Charlesworth – Similar to Adit Mohan's. Reason I didn't post mine is bc his is shorter.
No I don't think so.
Using basic geometry I proved that the length of diagonal PR is 2 and applying Pythagoras theorem found the length of base SR to be the square root of 3 i.e 1.732 . Hence , the area of the rectangle should be 1.732 . Both methods employed solving this problem are mathematically sound , yet there is difference in answers . Could you please tell me why ...
Log in to reply
I'm curious about how you found that the diagonal has length 2. I'm still quite certain of my answer, but I sense that there may be a more elegant solution method. If you could provide a few details about the basic geometry you used then I would have a better chance of determining why our answers differ.
Log in to reply
If you join the points P , Q , R and S to the point (lets call it O) of intersection of the two circles in the rectangle , you get three triangles POS , SOR and QOR . Also you'd have to draw a perpendicular from O to the base SR (let the point of intersection be M) . Since SOR is an isosceles triangle , the perpendicular is also the median which divides the angle SOR equally into two parts . In right triangle SOM , the sum of the angles OSM and SOM (let's call them a and b respectively) is 90 .
Also , lines PS and SM are parallel (since they're both perpendicular to the same line segment SR) .
This implies that anglePSO = angleSOM = b (alternate angles)
Triangle POS is also an isosceles triangle (SP=SO=1) . Therefore angles SPO and POS are equal (let SPO = POS = c). Hence , 2c+b=180 ...........(1)
Also , triangles SOM and ROM are congruent which in turn implies that triangles POS and QOR are congruent .
Therefore , angles POS and QOR are equal . (This makes them vertically opposite angles ) Hence , Points P , O and R lie on a straight line . Recall , SM is the median of triangle SOR and hence divides angle SOR equally into two parts . ( angle SOM = angle ROM =b)
Since P , O and S are points on a line ; angle ROM +angle SOM +angle POS = 180 i.e. 2b+c = 180 ...........(2)
Adding and subtracting equations (1) & (2) , we get ; b+c = 120 and b=c = 60 . Hence , POS is equilateral . Which implies that PO = 1 .
PR = PO + OR = 1+1 = 2 .
Log in to reply
@Gary Monteiro – I checked again and the error I committed was in assuming angles POS and angles QOR to be vertically opposite angles .
Log in to reply
@Gary Monteiro – O.k., great, thanks for clarifying. Your proof had me for a moment until I noticed the same error that you did. :)
I also got 1.732. I used similar triangles and properties of diagonals of rectangle.
Log in to reply
Could you please provide more details of your approach, Abhineet. I'm curious about how both you and Gary came to an answer of 3 .
Log in to reply
@Brian Charlesworth – I had thought of using calculus too like you did as it felt relevant. But then again, I am yet to get used to thinking of applying all the math to these online questions which I somehow feel must be done with minimalistic ways. So, we know that diagonals in rectangle bisect each other. If I join P and R or Q and S, it 'seemed' to pass right from the point where A and B are separated. It also 'seemed' to make sense because the region Guiseppi marked B is actually half of the area lost in partial overlap of circles. I then could establish that triangle PSR and OHR are similar, H is the pint of intersection of perpendicular from O to SR. This meant that PS/OH = PR/OR which made OH = 0.5. Now I established theta, the angle OSR, and could find SH[or HR, equivalently] with cos 30, doubled it to find the length and hence the area by A = LB. Only thing I think I was wrong at was supposing that O coincides with mid-point of diagonals.
Log in to reply
@Abhineet Sharma – Thanks for clarifying. Yes, I too always look for a minimalist way first, and this problem looks like it should have a simple, geometric solution, but I just can't see one. That's why this is a great problem - I keep thinking that there must be a more elegant solution.
@Abhineet Sharma – The diagram was not drawn to purport the criteria, but to be used only as a guide for clarification purposes.
Log in to reply
@Guiseppi Butel – I know. That is mostly understood. But, sometimes it is tempting too! :p I got it the hard way when my answer was not found right! Thanks for replying anyway.
@Brian Charlesworth – It seems that they assumed that PO = 1
Log in to reply
@Guiseppi Butel – Apparently. :)
This is great problem; thanks for posting it. I'm still wondering if this can be solved without calculus, or at least without resorting to WolframAlpha, (or the like).
Log in to reply
@Brian Charlesworth – I solved it with an Excel Spreadsheet.
How did you get the length of the diagonal to be 2?
Log in to reply
If you join the points P , Q , R and S to the point (lets call it O) of intersection of the two circles in the rectangle , it can be proved that the triangle POS is an equilateral triangle and the points P , O and R lie on a straight line .
PR=PO +OR
But , PO=PS=SO=1 (Since POS is equilateral ) .
And OR = 1 (Radius of the circle)
Therefore PR=2
Log in to reply
@Gary Monteiro – The only situation where PR = 2 is when OM = .5 or <ORS = 30 degrees.
At that angle, the area of B = .359694 the area of A. This does not fit the problem's criteria.
length of pr can never be 2?
how did you prove pr to be 2??
This my solution using basic geometry and algebra.
the intersection point of circles be X.(the intersection bw areas). all angles are in radians so pi conviniently cancels.
(area of B)/2=sector - triangle=.
(angle<XSR)/2-(sin<XSR)(cos<XSR)/2.
similarly.
(area of A/2)=(1-cos<PSX)(sin<PSX)-(<PSX/2-cos<PSX.sin<PSX/2).
<PSX=Pi/2-<XSR.
replacing to bring everything in terms of <XSR and inserting area of A=2B we have. LET <XSR=Y.
Y-(sinY)(cosY)=(cosY)(sinY)/2+(1-sinY)(cosY)-pi/4+Y/2 eq1.
notice that 2cosY is the answer.
Solving eq 1 for 2cosY (we'll need a calculator for this one) we get 1.6856.