Area Of A Strange Quadrilateral
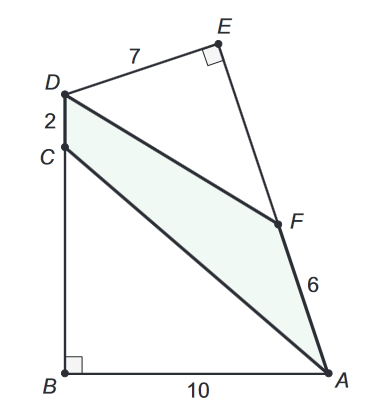
In the picture, the points C and F are in the sides BD and AE of the quadrilateral ABDE , respectively.
ABC and DEF are right angles and the segments AB , CD , DE and FA have their lengths in the picture. What is the area of the quadrilateral ACDF ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If we draw a line between points D and A, the area ACDF will be divided in two triangles.
The first triangle has a base of 6 and a height of 7. Then, its area is 21.
The other triangle has a base of 2 and an height of 10. Then, its area is 10.
Then, the area of the quadrilateral ACDF is 1 0 + 2 1 = 3 1 .