Area of a tilted curved square!

Calculus Level pending

Consider the following figure:

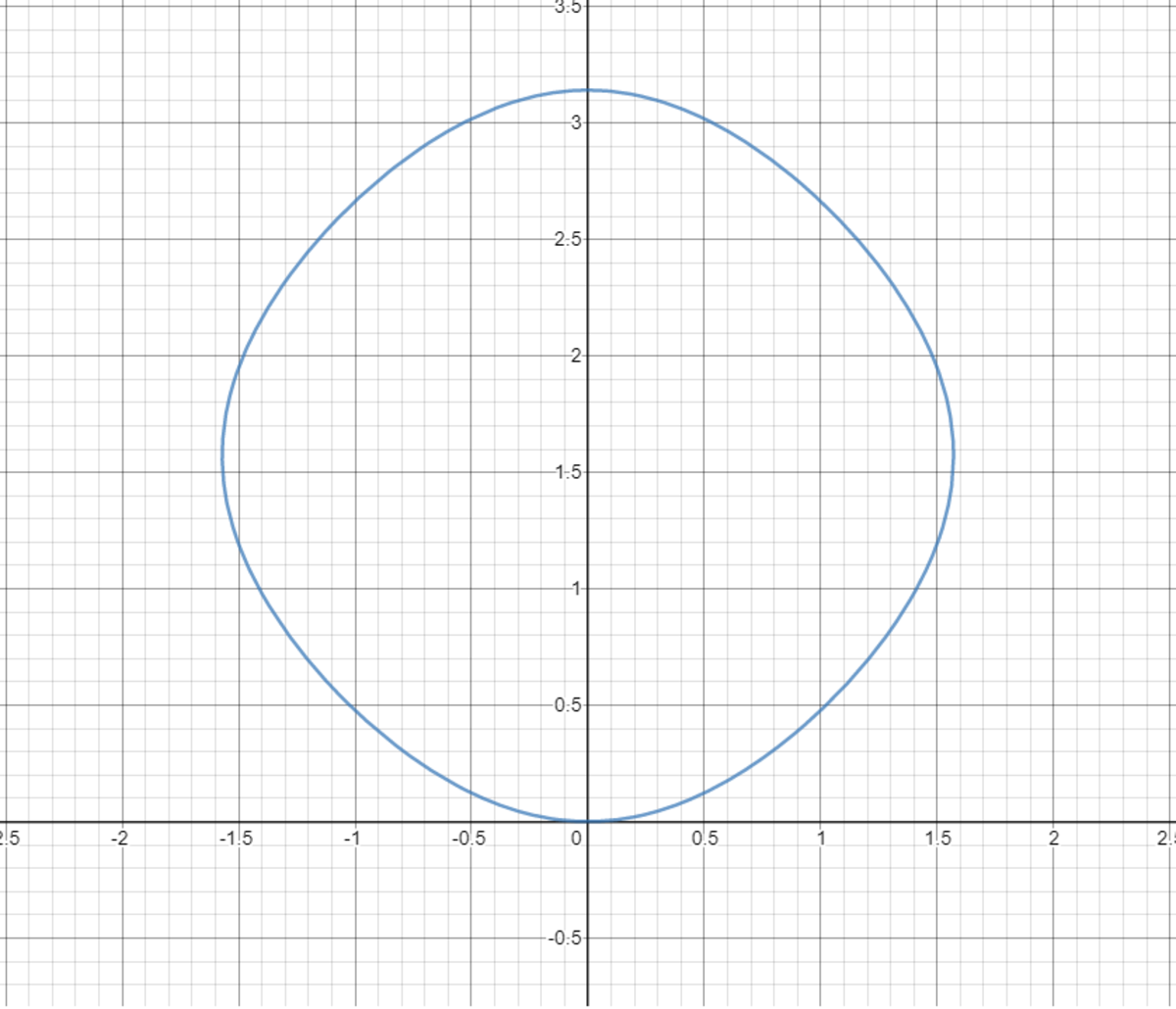
If the bottom right quadrant of the figure is represented by:

$\cos x + \sin y = 1$

Find the area enclosed by the figure.

The answer is 7.29488040109.

3 solutions

Steven Chase
Oct 22, 2020

This is a great one for Monte Carlo integration. Populate a million points randomly and uniformly within the red rectangle. Keep a count of how many points lie within the curved square $(\cos x + \sin y > 1 )$ . Find the ratio of the number of points within the curved square to the total number of points within the rectangle (the latter number includes points within the curved square). Multiply this ratio by the red rectangle area to get the area of the curved square.

import math
import random

N = 10**7
Aref = 4.0*3.5

count = 0

for j in range(0,N):

    x = random.uniform(-2.0,2.0)
    y = random.uniform(0.0,3.5)

    q = math.cos(x) + math.sin(y)

    if q > 1.0:
        count = count + 1

ratio = float(count)/float(N)

A = ratio*Aref

print N
print ratio
print A

#>>> 
#10000000
#0.5209745
#7.293643
#>>> ================================ RESTART ================================
#>>> 
#10000000
#0.521049
#7.294686
#>>> ================================ RESTART ================================
#>>> 
#10000000
#0.5210283
#7.2943962
#>>> ================================ RESTART ================================
#>>> 
#10000000
#0.5208348
#7.2916872
#>>> ================================ RESTART ================================
#>>> 
#10000000
#0.520857
#7.291998
#>>>

Your final answer still fluctuates in the 3rd decimal place. How are you able to determine that this estimate is sufficiently accurate?

Pi Han Goh - 7 months, 3 weeks ago

I have re-uploaded the result with ten million points. The results vary by less than one part in a thousand.

Steven Chase - 7 months, 3 weeks ago

You could increase your accuracy by just focusing on the square $[ \pi/2 , \pi /2]^2$ . This is because this closed figure is symmetric about $x = \pi/2$ and $y = \pi /2$ .

Pi Han Goh - 7 months, 3 weeks ago

I find it more helpful to just evaluate the definite integral $\displaystyle 4 \int _0^1 \frac{ \cos^{-1} (1-z)}{\sqrt{1-z^2}} \, dz \approx 7.29488$ via numerical approximation.

Pi Han Goh - 7 months, 3 weeks ago

@Pi Han Goh - that integrand doesn't look very well behaved near $z=0$ - how did you integrate it numerically?

If you translate $y$ by $-\frac{\pi}{2}$ , the function becomes $\cos x+\cos y=1$ which is symmetric about both the $x$ and $y$ axes.

The form of the area you then get is $4\int_0^{\frac{\pi}{2}} \cos^{-1} (1-\cos x) \; dx$

I still had to do this numerically, though.

Chris Lewis - 7 months, 3 weeks ago

Sorry, I've fixed my integrand in my previous comment already. Confirmation

I'm very skeptical to find an elementary closed form for this integral.

How did I integrate numerically? Well, I didn't. I just cheated by just summoning WolframAlpha. But I'm pretty sure we can solve this via midpoint rule/trapezoidal rule/simpsons rule/etc. Let me know if you want me to try it out on Python...

I tried expanding the integrand as the product of the Maclaurin series(es, plural?) of $\cos^{-1} (1-z)$ and $\frac1{\sqrt{1-z^2}}$ . But even after expanding over 30 terms, I can barely get a decent approximation.

Pi Han Goh - 7 months, 3 weeks ago

Update again: I've fixed my integrand yet again because mistakes everywhere.

Pi Han Goh - 7 months, 3 weeks ago

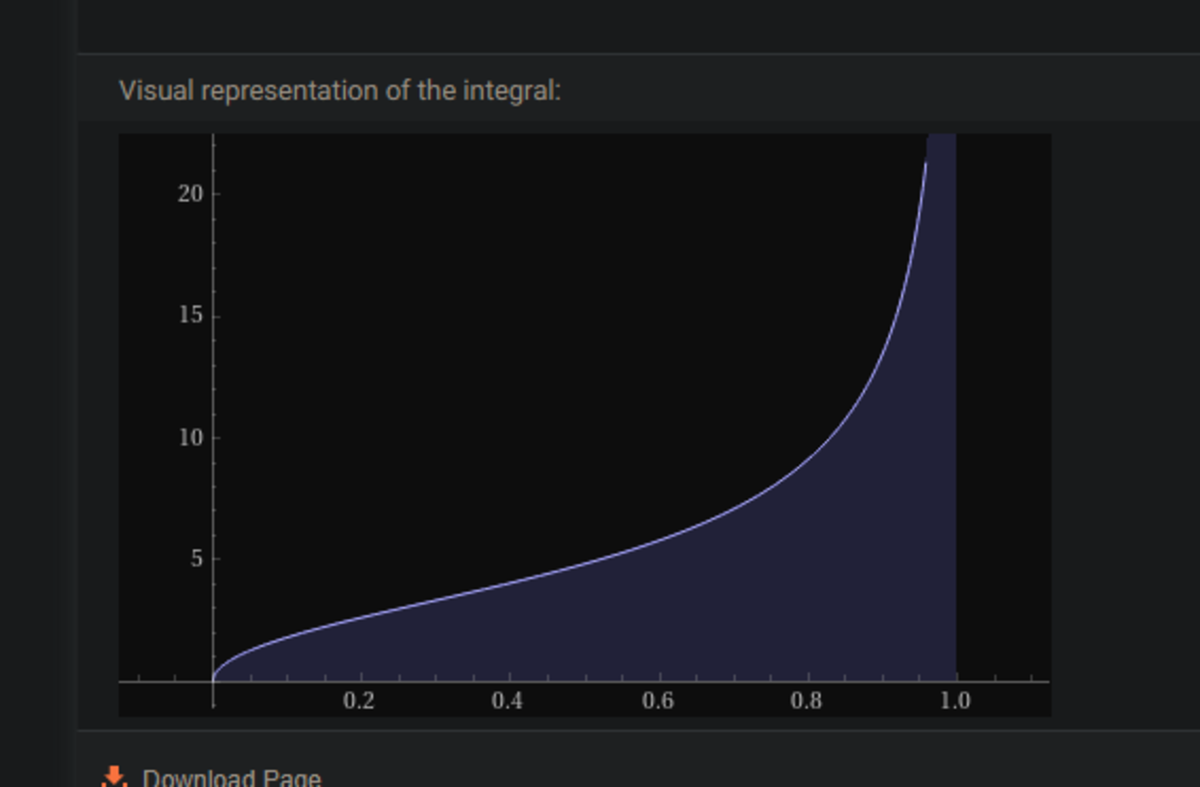
Well..... the integrand diverges at $z=1$ . No wonder my numerical approximation fails. I guess Monte-Carlo is the ONLY approach? Let me fire up my MC code now.

Pi Han Goh - 7 months, 3 weeks ago

from math import pi, cos, sin
from random import random as rd

# Let us just focus on the interval [0, pi/2]^2 only. As we just need to multiply the area of this region by 4
def given_function(these_two_numbers):
    '''
    Given a list of two idependent random numbers drawn from the interval [0, pi/2].
    Let's call these two numbers X and Y. We return the value cos(X) + sin(Y)
    '''
    return cos(these_two_numbers[0]) +  sin(these_two_numbers[1])

inside_frequency = 0 ; total_number_of_trials = int(1e7) # 10 million trials

for _ in range(total_number_of_trials):
    # Create two random numbers in the interval [0, pi/2]
    two_random_numbers = [ rd() * pi/2 for _ in range(2)]

    if given_function(two_random_numbers) >= 1:
        # If this sum is <= 1, then it falls inside the region of the enclosed figure.
        inside_frequency += 1

# We calculate the percentage of the success rate of these trials inside a square of [0, pi/2]^2
print(inside_frequency / total_number_of_trials * ((pi/2)**2) * 4)

# Sample result:            7.2905287270186925
# Theoretical result:       7.29488....

# Still a pretty dismal approximation if you asked me.

Pi Han Goh - 7 months, 3 weeks ago

@Pi Han Goh – The form of the integrand I put up doesn't behave too badly at either $x=0$ or $x=1$ (it's just the actual tilted square shape, so nothing too crazy there).

Does your numerical integration work better with that form?

$A=4\int_0^{\frac{\pi}{2}} \cos^{-1} (1-\cos x)\;dx$

Chris Lewis - 7 months, 2 weeks ago

@Chris Lewis – Just using trapezium rule, and dividing the interval into $10000$ steps, I got $A \approx 7.29488006934775$

(that was using Excel VBA, too, so probably not the best floating point arithmetic around!)

Chris Lewis - 7 months, 2 weeks ago

@Chris Lewis – I always wanted to learn VBA, but the Microsoft Office 365 package is a subscription plan, I wanted to buy a one-off plan that I can use until my prison of flesh completely decayed, but I noticed that the one-off plan doesn't have all the features. It sucks that all the services are now best on a subscription plan.

I'll submit a trapezoidal rule approach (or equivalent) if I ever come up with anything substantial. Be back soon.

Pi Han Goh - 7 months, 2 weeks ago

Jouko Juutistenaho
Apr 21, 2021

Easy to integrate 4*arcsin(1-cos(x)) from 0 to π/2 with Geogebra.

Pi Han Goh
Oct 30, 2020

Mathematica gave a more accurate answer.

Here's my Simpson's rule method:

from math import cos, acos, pi

# Let n denote the number of partitions. By Simpson's rule, n must be an even number
n = 10 ** 6
a = 0 ; b = pi /2 ; delta_x = (b-a)/n

# We want to generate all the coefficients [1,4,2,4,...,4,1] from the expression: (y0 + 4y1 + 2y2 + ... + 4y(n-1) + yn)
coefficients_in_front_y = [1] + [ 4 if index % 2 > 0 else 2 for index in range(1, n)] + [1]

def integrand_value(give_me_y):
    '''We want to calculate the integrand { 4 * arccos(1 - cos x) } for all y_k 's.
    '''
    return 4 * acos(1 - cos(give_me_y))

# Let us compute this part of the integral now: (y0 + 4y1 + 2y2 + ... + 4y(n-1) + yn)
this_integral = 0
for index in range(0, n + 1):
    this_coefficent = coefficients_in_front_y[index]
    this_y_value = a + delta_x * index
    if index == 0:
        this_integrand_value = 2 * pi
    elif index == n:
        this_integrand_value = 0
    else:
        this_integrand_value = integrand_value(this_y_value)
    this_integral += this_integrand_value

print(this_integral * delta_x) # Output: 7.294887316991251

I will try a stronger numerical approximation technique shortly. Maybe Gaussian quadrature ?

@Steven Chase @Chris Lewis

Pi Han Goh - 7 months, 2 weeks ago

# Using Chris Lewis method, int(0 to pi/2) 4 arccos(1 - cos x) dx, the integrand is always finite in its region, unlike my previous integral.

from math import pi, cos, acos
from random import uniform

def this_function(give_me_random_number): 
    ''' Compute the integrand { 4 * arccos(1 - cos x) } given a random input of x, where x ~ Uniform[0, pi/2]
    '''
    return 4 * acos(1 - cos(give_me_random_number))

inside_frequency = 0 ; total_number_of_trials = int(1e7) 

for _ in range(total_number_of_trials):
    # Create two random numbers in the intervals [0, pi/2] x [0, 2pi]
    two_random_numbers = [uniform(0, pi/2), uniform(0, 2 * pi)]
    # We first need to verify that the integrand is a one-to-one function, so the following condition can hold.
    if this_function(two_random_numbers[0] ) >= two_random_numbers[1]:
        inside_frequency += 1

# We calculate the percentage of the success rate of these trials inside the square [0, pi/2] x [0, 2 * pi]
print(inside_frequency / total_number_of_trials * (pi/2) * (2 * pi))

# Sample result:            7.294987814287105
# Theoretical result:       7.29488....

# Much better!

Pi Han Goh - 7 months, 2 weeks ago

Area of a tilted curved square!

The answer is 7.29488040109.

3 solutions

0 pending reports