Area Of An Irregular Pentagon

$G=AB \times CD, O=BC \times EG, K=BD \times AC, H=GE \times AD,$ G, O, K, H in one line. Because: $[CDE]=[BCD] => BE//DG => \frac{BK}{DK}=\frac{EK}{GK}$ $<=> \frac{OK}{KH} = \frac{2 \times KH}{2 \times KH + 2 \times OK}$ $<=> \frac{OK}{KH} = \frac{KH}{KH+OK}$ $=> OK^{2}+OK*KH=KH^{2} => \frac{OK}{KH}=\frac{\sqrt{5}-1}{2}$ $=> S(ABCDE)=S(ABE)+S(BEC)+S(CED)=12 \times {\frac{3 \times \sqrt{5} +5}{\sqrt{5}+1}} = 43.4164.$

$$ Let $\overrightarrow{AB}=x$ , then

$\begin{aligned} [\text{ABC}]&=\frac{1}{2}\cdot\overrightarrow{AB}\cdot\overrightarrow{BC}\cdot\sin 120^\circ\\ 12&=\frac{1}{2}\cdot x\cdot\overrightarrow{BC}\cdot\frac{1}{2}\sqrt{3}\\ \overrightarrow{BC}&=\frac{16\sqrt{3}}{x} \end{aligned}$

and it is easy to notice that $\Delta\text{ABC}\cong\Delta\text{BCD}$ , therefore $\overrightarrow{CD}=x$ . The rest sides are just history because all of them can easily be obtained. Take a look the picture below.

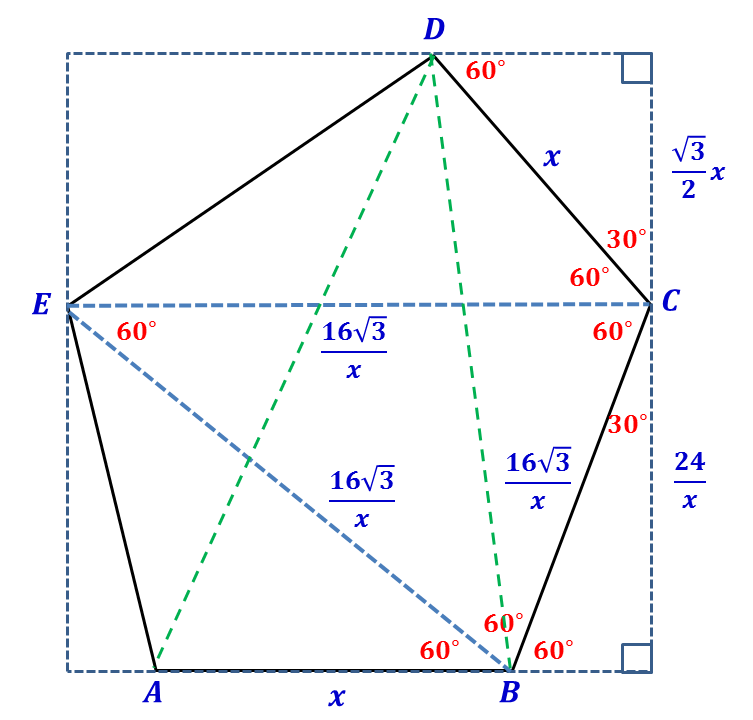Convex Pentagon

We can see that $[\text{ABD}]=[\text{BCE}]$ , therefore

$\begin{aligned} [\text{ABD}]&=[\text{BCE}]\\ \frac{1}{2}x\left(\frac{24}{x}+\frac{\sqrt{3}}{2}x\right)&=\frac{1}{2}\cdot\frac{16\sqrt{3}}{x}\cdot\frac{16\sqrt{3}}{x}\sin 60^\circ\\ 24+\frac{\sqrt{3}}{2}x^2&=\frac{384\sqrt{3}}{x^2}\\ \frac{\sqrt{3}}{2}x^4+24x^2-384\sqrt{3}&=0. \end{aligned}$

Although the last equation can be formed into quadratic equation, I prefer solving it by using Wolfram Alpha since calculator is allowed. We obtain $x\approx 4.138533594$ . Thus,

$\begin{aligned} [\text{ABCDE}]&=[\text{ADE}]+[\text{ABD}]+[\text{BCD}]\\ &=12+\frac{1}{2}x\left(\frac{24}{x}+\frac{\sqrt{3}}{2}x\right)+12\\ &=36+\frac{\sqrt{3}}{4}x^2\\ &\approx36+\frac{\sqrt{3}}{4}(4.138533594)^2\\ &\approx\boxed{\color{#3D99F6}{43.4\;\text{unit}^2}} \end{aligned}$

$$

---

$\text{\# }\mathbb{Q.E.D.}\text{ \#}$

Let $AB = x$ . Now $BE$ and $CD$ must be parallel (so that $[BCD]=[CDE]$ ) and $CE$ and $AB$ must be parallel (so that $[ABC] = [ABE]$ ). Thus $BCE$ is an equilateral triangle, and so the area of the pentagon is $24 + \tfrac14x^2\sqrt{3}$ .

Moreover $AD$ is parallel to $BC$ (so that $[ABC]=[BCD]$ ) and $AD$ is a distance $\tfrac{24}{x}$ from $BC$ . A bit of trig shows that $AD = x + \tfrac{16}{x}\sqrt{3}$ , while $E$ is a height $\tfrac12x\sqrt{3} - \tfrac{24}{x}$ above $AD$ . We obtain the equation $24 \; = \; \left(\tfrac12x\sqrt{3} - \tfrac{24}{x}\right)\left(x + \tfrac{16}{x}\sqrt{3}\right)$ which becomes $x^4 - 16\sqrt{3} x^2 - 768 \; = \; 0$ and hence $x^2 \,=\, 8\sqrt{3} \pm 8\sqrt{15}$ . Since $x^2$ is positive, $x^2 = 8\sqrt{3}(1+\sqrt{5})$ , and hence the pentagon area is $\tfrac14\sqrt{3}x^2 + 24 \; =\; 6(1+\sqrt{5}) + 24 \; = \; 6(5 + \sqrt{5}) \; =\; 43.4$ to $1$ decimal place.

Let $[ABC] = [BCD] = [CDE] = [DEA] = [EAB] = A_{0} = 12$ . The area of the pentagon writes: $[ABCDE] = [ABC] + [ACD] + [DEA] = 2A_{0} + [ACD] = 2A_{0} + [ABD] =$ $2A_{0} + [ACE] = 2A_{0} + [BCE] = 2A_{0} + [BDE]$ , from which $[ABD] = [ACD] = [ACE] = [BCE] = [BDE] = A_{1}$ . Thence: $[ABCDE] = 2 A_{0} + A_{1}$ .

Using the identity (see Note 2):

$[ABD] [ACE] = [ACD] [EAB] + [ABC] [DEA]$ ,

and making the appropriate substitutions,

$A_{1} A_{1} = A_{0} A_{1} + A_{0} A_{0}$ , solving into: $A_{1} = A_{0} (1 + \sqrt{5})/2$ . The other solution would apply only to the case of the concave (stellate) pentagon.

$[ABCDE] = A_{0} (5 + \sqrt{5})/2 = 43.4164$ .

NOTE 1: This solution does not make use of the given angles $\angle BCD = \angle ABC = 120^\circ$ . The total area of the pentagon is independent of these angles, once all the triangles at each vertice (formed with the two nearest neighbors vertices) have equal area. The given angles can have different values from $120^\circ$ , each a different value, and the total area is still given by the same relation $[ABCDE] = A_{0} (5 + \sqrt{5})/2$ .

NOTE 2: This identity is always valid for any five distinct points in the plane. It follows from the trigonometric identity: $\sin (a+b) \sin (b+c) = \sin (a+b+c) \sin (b)+ \sin (a) \sin (c)$ . Each side of this identity is equal to $[\cos (a-c)-\cos (a+2b+c)]/2$ . Multiply both sides of this identity by $(AB \cdot AC \cdot AD \cdot AE)$ , make $a=\angle BAC, b= \angle CAD$ , and $c=\angle DAE$ , use: $[ABC]=AB \cdot AC \sin (a)$ ; $[DEA]=AD \cdot AE \sin (c)$ ; $[EAB]=AB \cdot AE \sin (a+b+c)$ ; $[ACD]=AC \cdot AD \sin (b)$ ; $[ABD]=AB \cdot AD \sin (a+b)$ ; and $[ACE]=AC \cdot AE \sin (b+c)$ . The identity for the areas then follows.

$[ABCDE] = [ABCD] + [ADE]$

Let,

$AB = x$ and $BC = y$ .

AD || BC, because [ABC] = [DBC], so perpendicular distance of A from BC is the same as perpendiular distance of D from BC and both are on the same side of BC. This is the most important pair of parallel lines for this soln.

Thus,

$[ABC] = [DBC] \Rightarrow AD||BC$

$[EAB] = [CAB] \Rightarrow AB || EC$

$[ECD] = [BCD] \Rightarrow CD || EB$

Drop perpendiculars from B and C to AD, at F and G respectively.

$\angle BAD = \angle BDA = 60$

$\triangle ABF and \triangle DCG$ are 30-60-90 triangles, with $BF = CG$ and hence are congruent

$Thus, AB = CD = x$

Also,

$BF = CG = \frac { \sqrt { 3 } }{ 2 }x$ .... sides opposite 60

$Also, AF = DG = \frac { 1 }{ 2 }x$ .... sides opposite 30

$AD = AF + FG + GD$

$\therefore AD = AF + BC + GD$

$\therefore AD = \frac { 1 }{ 2 }x + y + \frac { 1 }{ 2 }x$

$\boxed{\therefore AD = x + y} \dots (1)$

$[ABC] = \frac{1}{2}*height*base = 12$

$= \frac{1}{2}*BF*BC = 12$

$= \frac{1}{2}*\frac { \sqrt { 3 } }{ 2 }x*y = 12$

$\boxed{ \therefore xy = 16\sqrt{3} } \dots (2)$

Let EB and EC intersect AD in H and K, respectively.

$CD||EB$ and $\angle BCD = 120 \Rightarrow \angle EBC = 60$

$AB||EC$ and $\angle ABC = 120 \Rightarrow \angle ECB = 60$

$\therefore \triangle EBC$ is an equilateral triangle.

Similarly,

$\angle ABE = \angle ABC - \angle EBC = 120 - 60 = 60$

$\angle ECD = \angle BCD - \angle BCE = 120 - 60 = 60$

$\therefore \triangle ABH$ and $\triangle CDK$ as equilateral triangles with side $x$ .

$\therefore AH = DK = x$

$\therefore AD = AH + HK + DK = x + HK + x = 2x + HK$

$But from (1), AD = x+y$

$\therefore x + y = 2x + HK$

$HK = y-x$

$\therefore HK || BC \Rightarrow \triangle EHK$ is also an equiliateral triangle of side $y-x$ .

$\therefore$ height of $\triangle EHK$ = height of $\triangle EAD = \frac { \sqrt { 3 } }{ 2 }(y-x)$

$[AED] = \frac{1}{2} *$ height * base

$\therefore [AED] = \frac{1}{2} * \frac { \sqrt { 3 } }{ 2 }(y-x) * (x+y)$

But $[AED] =12 \dots given$

$\therefore (y-x)(y+x) = 16 \sqrt{3}$

$\boxed{\therefore y^{2} - x^{2} = 16 \sqrt{3}} \dots (3)$

$Solving (1) and (2),we get$

$\boxed{x = 4.14}$

$\boxed{y = 6.7}$

$[ABCDE] = [ABCD] + [ADE] = [ABCD] + 12$

ABCD is a trapezium

$\therefore [ABCDE] = 12 + \frac {1}{2} * sum of parallel sides * height$

$\therefore [ABCDE] = 12 + \frac {1}{2} * (BC + AD) * (BF)$

$\therefore [ABCDE] = 12 + \frac {1}{2} * [(y) + (x+y)] * \frac{\sqrt{3}}{2}*x$

$\therefore [ABCDE] = 12 + \frac{\sqrt{3}}{4}[2y + x]*x$

$\therefore [ABCDE] = 12 + \frac{\sqrt{3}}{4}[2(6.7) + 4.14]*4.14$

$\boxed{ \therefore [ABCDE] = 43.44}$

If someone can guide me on attaching an image to a solution, I'll upload the diagram as well. The changes aren't a lot. You just need to join the 5 vertices to each other. And drop perpendiculars BF and CG from B and C, respectively, to AD.

$[ABC]=[BCD] \Longrightarrow AD\parallel BC$

$[BCD]=[CDE] \Longrightarrow BE\parallel CD$

$[EAB]=[ABC] \Longrightarrow EC\parallel AB$

Let's call x the length of BC and h the distance between AD and BC.

$[ABC]={xh\over2}\Longrightarrow{xh\over2}=12\Longrightarrow h={24\over x}$

Let's call L the intersection of AD and EC. Triangle LDC is equilateral, so:

$(LD)={h\over{\sqrt3\over2}}\Longrightarrow(LD)={48\over x\sqrt3}$

$(AD)=(AL)+(LD)=x+{48\over x\sqrt3}$

Let's call d the distance of E from AD.

$[EAD]={(AD)d\over2}\Longrightarrow{(AD)d\over2}=12\Longrightarrow d={24\over(AD)}\Longrightarrow d={24\over x+{48\over x\sqrt3}}\>\>\>(1)$

Triangle EBC is equilateral, so the distance of E from BC is ${x\sqrt3\over2}$ . Hence:

$d={x\sqrt3\over2}-h={x\sqrt3\over2}-{24\over x}\>\>\>(2)$

From (1) and (2) I take the equation:

${24\over x+{48\over x\sqrt3}}={x\sqrt3\over2}-{24\over x}\iff$

$\iff\left(x+{48\over x\sqrt3}\right)\left({x\sqrt3\over2}-{24\over x}\right)=24\iff$

$\iff x^2{\sqrt3\over2}-24+{48\over2}-{48\cdot24\over x^2\sqrt3}=24\iff$

$\iff x^2{\sqrt3\over2}-{2\cdot24^2\over x^2\sqrt3}=24\iff$

$\iff x^2{\sqrt3\over2}-24-{2\cdot24^2\over x^2\sqrt3}=0\iff$

$\iff{\sqrt3\over2}x^4-24x^2-{2\cdot24^2\over\sqrt3}=0\>\>\>(3)$

$D=24^2+4\cdot{\sqrt3\over2}\cdot{2\cdot24^2\over\sqrt3}=24^2+4\cdot24^2=5\cdot24^2$

$(3)\iff x^2={24\pm\sqrt{5\cdot24^2}\over2\cdot{\sqrt3\over2}}\iff$

$\iff x^2={24\pm24\sqrt5\over\sqrt3}\iff$

$\iff x^2={24\over\sqrt3}\left(1\pm\sqrt5\right)\buildrel{x^2\ge0}\over\iff$

$\iff x^2={24\over\sqrt3}\left(1+\sqrt5\right)\iff$

$\iff x^2={24\sqrt3\over3}\left(1+\sqrt5\right)\iff$

$\iff x^2=8\sqrt3\left(1+\sqrt5\right)\buildrel{x\ge0}\over\iff$

$\iff x=\sqrt{8\sqrt3\left(1+\sqrt5\right)}\approx6.696$

$(BC)=x\approx6.696$

$(AD)=x+{48\over x\sqrt3}\approx10.835$

$h={24\over x}\approx3.584$

$[ABCDE]=[ABCD]+[ADE]={(AD)+(BC)\over2}\cdot h+[ADE]$

So

$[ABCDE]\approx{10.835+6.696\over2}\cdot3.584+12=\boxed{43.416}$